Теория Мат Анализа. Теория Мат Анализ. Сформулировать основные виды неопределенностей и способы их раскрытия. Асимптотические формулы. Привести примеры

• Название: Сформулировать основные виды неопределенностей и способы их раскрытия. Асимптотические формулы. Привести примеры
• Анкор: Теория Мат Анализа
• Дата: 14.05.2023
• Размер: 1.81 Mb.
• Имя файла: Теория Мат Анализ.docx
• Тип: Документы; #1128125

1. 
   Сформулировать основные виды неопределенностей и способы их раскрытия. Асимптотические формулы. Привести примеры
   

• 
  Деление 0 на 0
  

Преобразование и последующее упрощение выражения. Если выражение имеет вид  sin(kx)kxsin(kx)kx или kxsin(kx)kxsin(kx) то нужно использовать первый замечательный предел. Если такое решение не подходит, пользуемся правилом Лопиталя или таблицей эквивалентных бесконечно малых выражений

• 
  Деление бесконечности на бесконечность/
  

Преобразование и упрощение выражения либо использование правила Лопиталя

• 
  Умножение нуля на бесконечность или нахождение разности между двумя бесконечностями
  

Преобразование в 0/0 или бесконечность/бесконечность с последующим применением правила Лопиталя

• 
  Единица в степени бесконечности
  

Использование второго замечательного предела

Асимптотические формулы.

Теорема. Если  , то  , где  , т.е. функция   является бесконечно малой функцией при  . Верно и обратное утверждение: если  , где   - бесконечно малая функция при  , то  .

Рассмотрим первый замечательный предел  . Тогда  , при этом  . Используя полученную формулу, представим функцию   в виде  . Так как   (действительно  ), перепишем найденную формулу в виде  .

Подобные формулы, которые называют асимптотическими формулами

1)  ;

2)  ;

3)  ,

;

4)  ;

2. 
   Непрерывность функции. Точки разрыва, их классификация
   

• 
  Функция у = f(x) называется непрерывной в точке   , если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.   .
  
• 
  Функция у=f(x) называется непрерывной в точке   , если она определена в точке хо и ее окрестно­сти и бесконечно малому прираще­нию аргумента соответствует бесконечно малое приращение функции, т.е.   .
  

Точками разрыва функции называются точки, в которых функция не обладает свойством непрерывности.

Классификация точек разрыва:

1. Точки разрыва первого рода (скачок) – точка   если фукнция имеет конечные но не равные односторонние пределы. (   )

Пример:     неравные односторонние пределы (разрыв первого рода).

2. Точки разрыва второго рода (бесконечный разрыв) - очка   если хотя бы один из односторонних пределов бесконечен или несуществует.

Примет: 

3. 
   Таблица основных производных.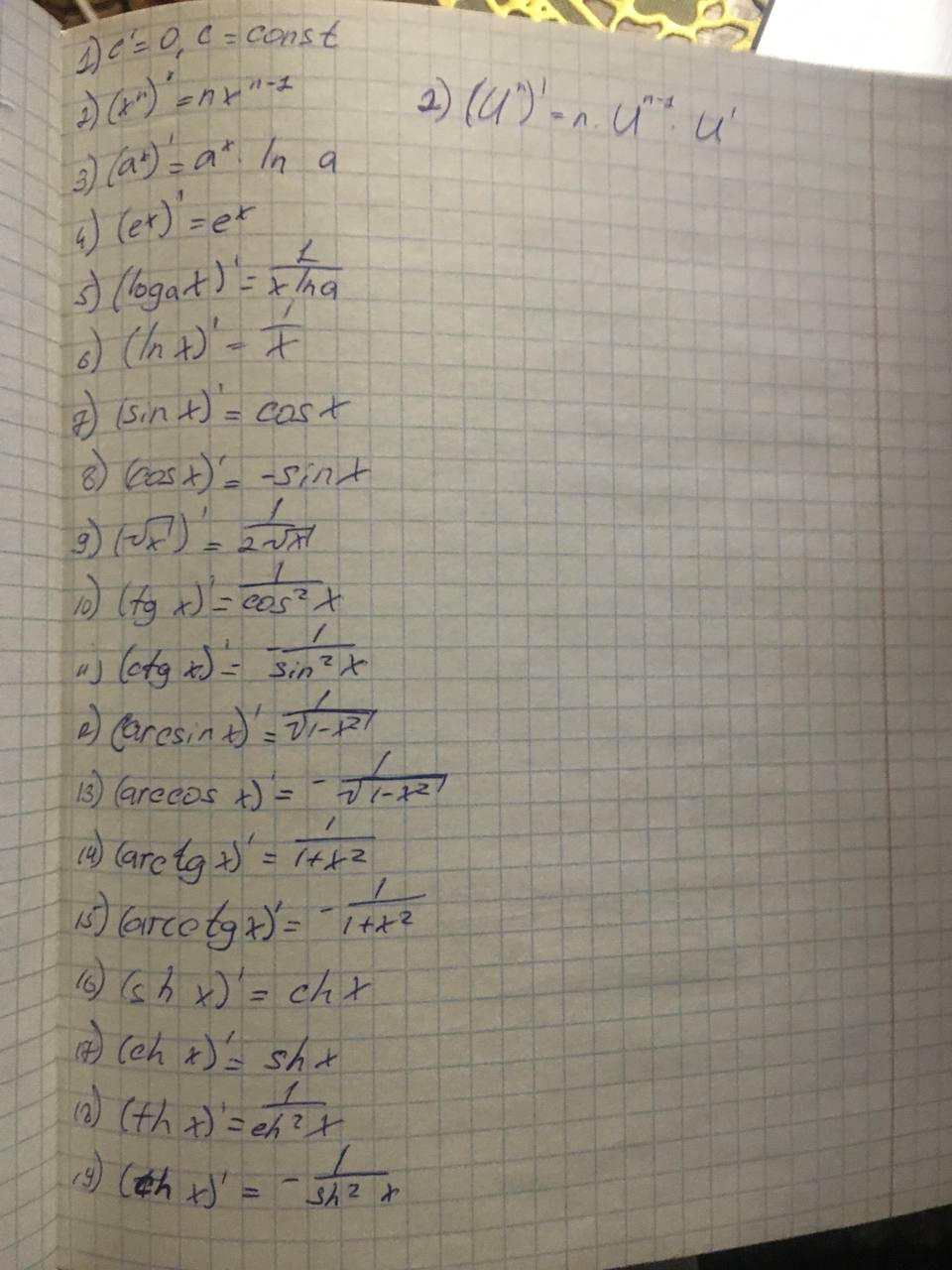
   

4. 
   Производная функции, заданной через параметр. Производная неявной функции
   

Зависимость функции y от аргумента x может осуществляться через посредство третьей переменной t, называемой параметром: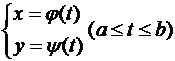




В этом случае говорят, что функция y от x задана параметрически. Параметрическое задание функции удобно тем, что оно дает общую запись для прямой и обратной функций.
Предположим, что на некотором промежутке функции x=φ(t) и y=ψ(t) имеют производные, причем φ’(t)≠0. Кроме того, для x=φ(t) существует обратная функция x^-1 = t(x) (производная обратной функции равна обратной величине производной прямой функции).
Тогда y(x)=ψ(t(x)) – сложная функция и ее производная: 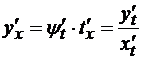 . Производную тоже запишем в параметрической форме: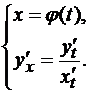



Пусть дано уравнение F(x,y)=0, не разрешенное относительно y. Если существует y=f(x) такая, что F[x,f(x)]=0, то говорят, что уравнение F(x,y)=0 задает y как функцию от x неявно. Обычное задание функции y=f(x) называют явным.

   – пример неявной функции.

5. 
   Таблица основных первообразных. Основные методы интегрирования.
   

Наиболее важными методами интегрирования являются:

1) метод непосредственного интегрирования (метод разложения),

2) метод подстановки (метод введения новой переменной),

3) метод интегрирования по частям.

6. 
   Приложение определенного интеграла
   

7. 
   Несобственные интегралы 1го и 2го рода
   

Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен, а подынтегральная функция ограничена на нем — в противном случае множество сумм Дарбу не будет ограниченным. При решении задач встречаются случаи, когда одно или оба из этих условий не выполняются, т. е. когда промежуток интегрирования бесконечен или подынтегральная функция не ограничена. Такие интегралы называются несобственными. Различают несобственные интегралы 1-го и 2-го рода в зависимости от того, имеем ли мы дело с бесконечностью промежутка интегрирования или с неограниченностью подынтегральной функции.

8. 
   Функции нескольких переменных. Частные производные. Полный дифференциал. Экстремум ФНП.
   

Переменная z называется функцией двух переменных x и y , если по некоторому вполне определенному закону каждой упорядоченной паре чисел  x, y) из некоторого множества ставится в соответствие вполне определенное значение z.

Дадим аргументу   приращение  , аргументу   — приращение   Тогда функция   получит наращенное значение   Величина   называется полным приращением функции в точке   Если задать только приращение аргумента   или только приращение аргумента  , то полученные приращения функции соответственно  называются частными.

Если функция   дифференцируема, то полный дифференциал ее имеет вид)



где



Как и в случае одной переменной, функция   имеет узловые, определяющие структуру графика точки. В первую очередь это точки экстремума.