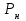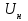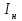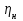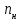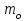Лабораторная работа 1. Синтез модального регулятора и расчет переходных процессов в электроприводе постоянного тока
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
Тема работы: Синтез модального регулятора и расчет переходных процессов в электроприводе постоянного тока Цель работы заключается в изучении системы управления электроприводом постоянного тока с модальным регулятором координат на примере электропривода бурового станка. Общие сведения Структурная схема электропривода постоянного тока вращателя бурового става с модальным регулятором представлена на рис.1. 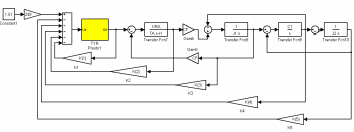 Рис. 1. Структурная схема с модальным регулятором. Методические указания Отрицательная обратная связь по координате объекта управления (ОУ) стабилизирует эту координату. Поэтому, если замкнуть ОУ по всем координатам, характеризующим его состояние в любой момент времени и называемым переменными состояния, то при соответствующем подборе коэффициентов обратных связей можно получить желаемые характеристики объекта управления относительно выходных координат. В общем случае ОУ имеет несколько: - входов U1, U2, …, Um; - выходов y1, y2, …, yr; - переменных состояния х1, х2, …, хn, где n - равно числу независимых дифференциальных уравнений, описывающих динамику ОУ . Сигналы обратных связей суммируются в модальном регуляторе в сигналы, образующие вектор UР(t) = [uр1, up2, …, upm]T, который подается на входы объекта управления, где вычитается из вектора задающих сигналов V(t) = [v1,v2, …,vm]T, в результате чего образуется вектор управляющих сигналов U(t) = [u1, u2, …, um]. Объект управления описывается системой дифференциальных уравнений в форме Коши: 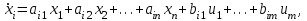 где i = 1, …, n; 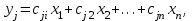 где j = 1, …, r. Уравнение модального регулятора и уравнение замыкания 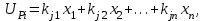 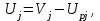 где j = 1, …, m. В матричной форме данные уравнения представляются в следующей форме: 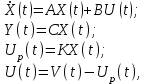 (1) (1)где А – квадратная матрица объекта управления ( 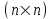 с элементом аij; с элементом аij; В – матрица управления 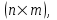 с элементом вij; с элементом вij;C – матрица выходов 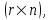 с элементом сij; с элементом сij;K – матрица модального регулятора 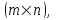 с элементом кij. с элементом кij.Проведя ряд преобразований с системой уравнений, получим результирующее матричное уравнение во временной области: 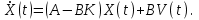 (2) (2)Уравнение (2) в операторной форме имеет вид 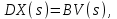 (3) (3)где D – характеристическая квадратная матрица 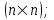 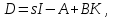 (4) (4) где I – единичная матрица. Детерминант от матрицы D является характеристическим полиномом замкнутого по вектору состояния объекта управления: 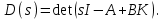 (5) (5)Решение характеристического уравнения D(s)=0 дает корни ОУ, замкнутого по вектору состояния. Отсюда вытекает принцип синтеза модального регулятора: подобрать матрицу К модального регулятора так, чтобы получить в комплексной плоскости желаемое распределение корней характеристического полинома замкнутого по вектору состояния объекта управления. Синтез МР выполняется методом стандартных уравнений, которые в нормированной форме приведены в справочной литературе. Процедура выполнения синтеза МР методом стандартных уравнений осуществляется в тир этапа: - определение количества и выбор переменных состояния, составление относительно выходной координаты характеристических уравнений для разомкнутого и замкнутого по вектору состояния ОУ; - выбор по желаемым показателям качества нормированного уравнения, порядок которого равен порядку уравнения ОУ; - определение параметров МР из системы уравнений 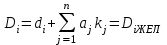 , (6) , (6)где i = 1,…, n. Синтез МР для приведенной системы электропривода (рис. 1) выполняется с использованием специальной программы в среде MATLAB «Вычисление коэффициентов оптимального регулятора [K]=lqry(sys,0.06,0.01)». Согласно процедуре синтеза выбираются переменные состояния: 1 - х1 = еП – ЭДС на выходе тиристорного преобразователя; 2 – х2 = iЯ - ток якоря двигателя; 3 – х3 = ω1– частота вращения якоря двигателя; 4 – х4 = М12– момент статических сопротивлений рабочего органа; 5 – х5 = ω2– частота вращения рабочего органа. Далее составляются уравнения состояния, описывающих систему в форме Коши: 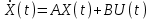 или в алгебраической форме: или в алгебраической форме: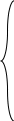 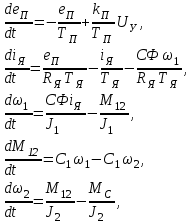 (7) (7)где ТП = Тμ – электромагнитная постоянная времени тиристорного преобразователя. В соответствии системы уравнений (7) формируются матрицы А, В, С, D.     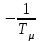 0 0 0 0 0 0 0 0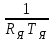 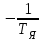 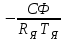 0 0 0 0А = 0 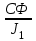 0 0 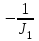 0 0 0 0 С1 0 - С1   0 0 0 0 0 0 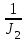 0 , 0 , В =[ 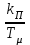 0 0 0 0 ], С = [0 0 0 0 1], D = [0]. 0 0 0 0 ], С = [0 0 0 0 1], D = [0].Для расчета параметров модального регулятора необходимо создать m-файл, пример которого приведен ниже. % Расчет оптимального регулятора для привода постоянного тока % Исходные данные % Двигатель 4ПФ160М P=22кВт CF=3.393; RA=0.6; TA=0.0141; J1=1.2; J2=0.0496; C1=9895.2; Tm=0.01; Kost=0.001; Un=440; Kp=Un/10; % Динамическая система в пространстве состояний % dx/dt=Ax+Bu; % y=Cx+Du; A=[-1/Tm 0 0 0 0; 1/(RA*TA) -1/TA -CF/(RA*TA) 0 0; 0 CF/J1 0 -1/J1 0; 0 0 C1 0 -C1; 0 0 0 1/J2 0] B=[Kp/Tm; 0; 0; 0; 0] C=[0 0 0 0 1] D=[0] % Сохранание динамической системы в пространстве состояний % под именем sys sys=ss(A,B,C,D) % Вычисление коэффициентов оптимального регулятора [K]=lqry(sys,0.06,0.01) Ход работы 1. Проведем необходимые расчеты параметров электропривода в соответствии: Исходные данные для расчета параметров приведены в табл. 1. Таблица 1 Характеристики двигателя
При расчете принимаются следующие параметры: 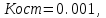 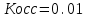 , , 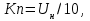 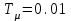 . . Расчет параметров двигателя: 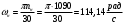 ; ;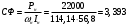 ; ;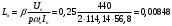 ; ;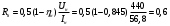 ; ;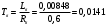 ; ; где р - число пар полюсов (принять р=2), 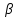 - коэффициент (принять - коэффициент (принять 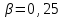 ). Момент инерции якоря двигателя ). Момент инерции якоря двигателя 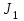 принять равным от 1 до 3, причем машинам меньшей мощности соответствует меньшее значение момента инерции. принять равным от 1 до 3, причем машинам меньшей мощности соответствует меньшее значение момента инерции.2. Рассчитаем параметры регуляторов согласно методике, приведенной в методических указаниях. 3. Провести моделирование привода и уточнить настройки регуляторов по наилучшему протеканию переходных процессов. На входе сигнала задания сигнал должен нарастать плавно от нуля до номинального значения за 1-2 секунды. 4. Рассчитаем параметры механической части привода. - полярный момент сечения 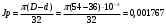 , ,где D - наружный диаметр буровой трубы; d - внутренний диаметр буровой трубы трубы. - крутильную жесткость буровой трубы 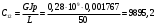 , ,где G - модуль сдвига; L = 50м – длина бурового става. - момент инерции бурового става 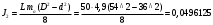 , ,где m0 - масса погонного метра трубы. Таблица 2 Параметры трубы
I. Переходные процессы при номинальной нагрузке: 1) Сигнал на выходе с тиристорного преобразователя 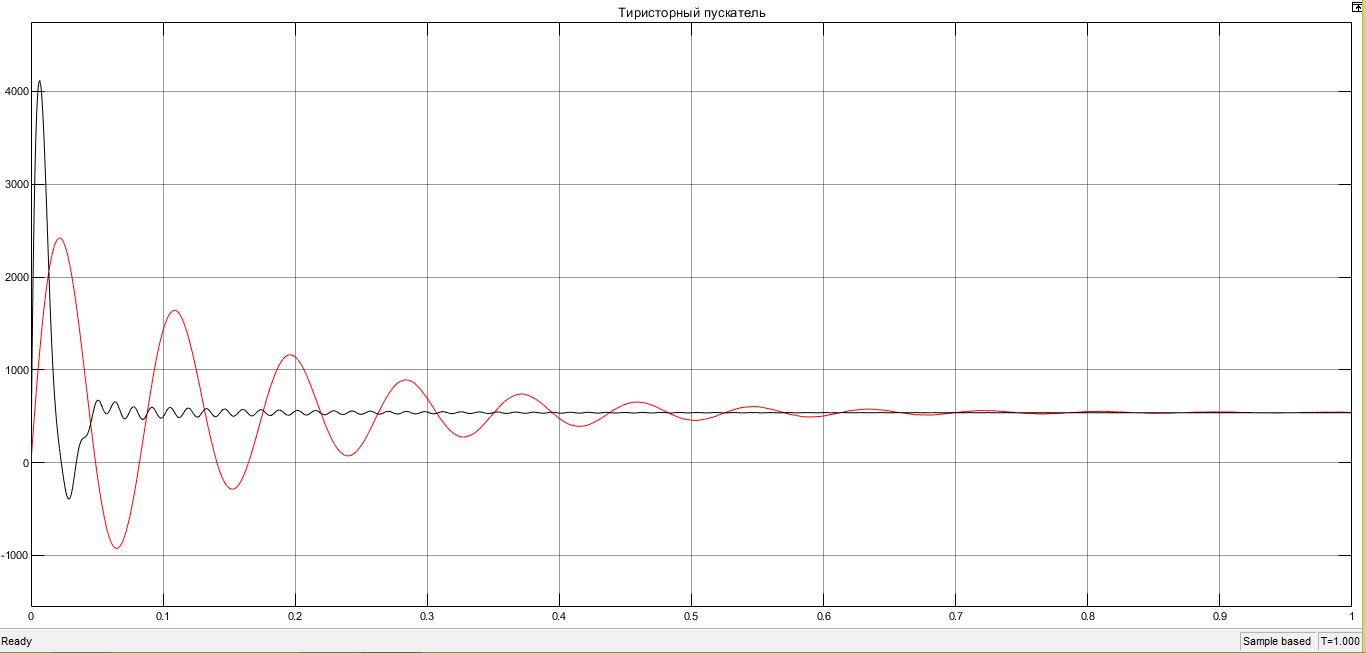 Рис. 2. Напряжение на тиристорном пускателе 2) Токи в двигателе: 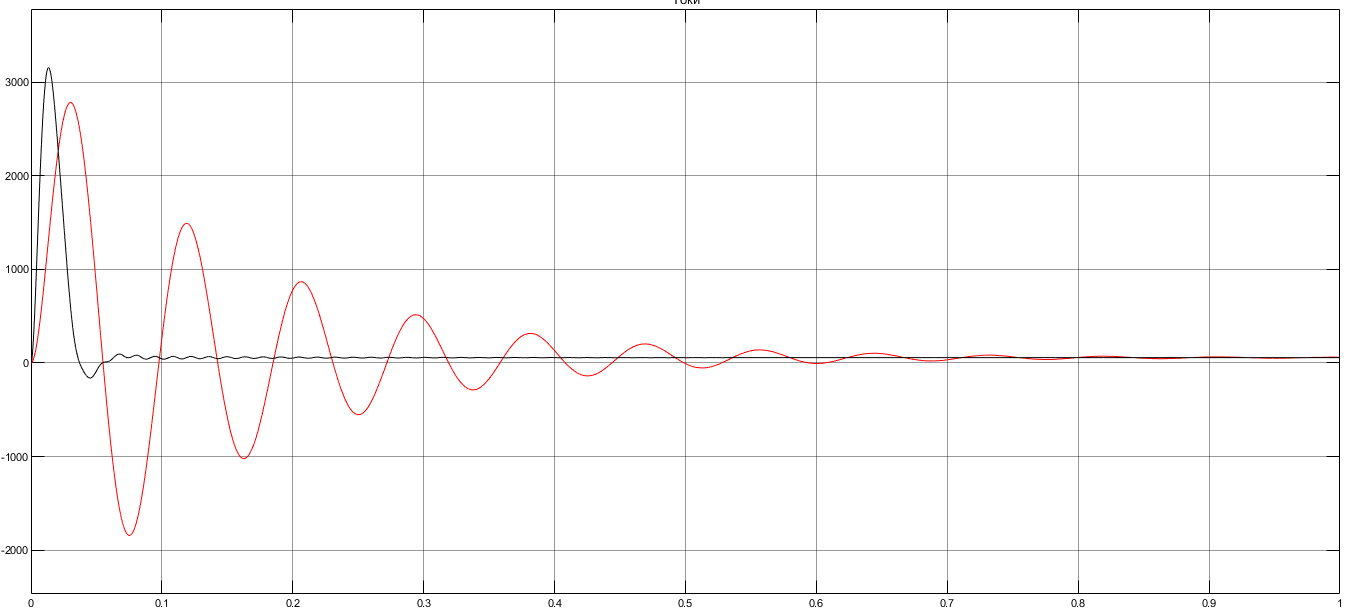 Рис. 3. Токи в обмотках двигателя 3) Сигнал по скорости на валу двигателя: 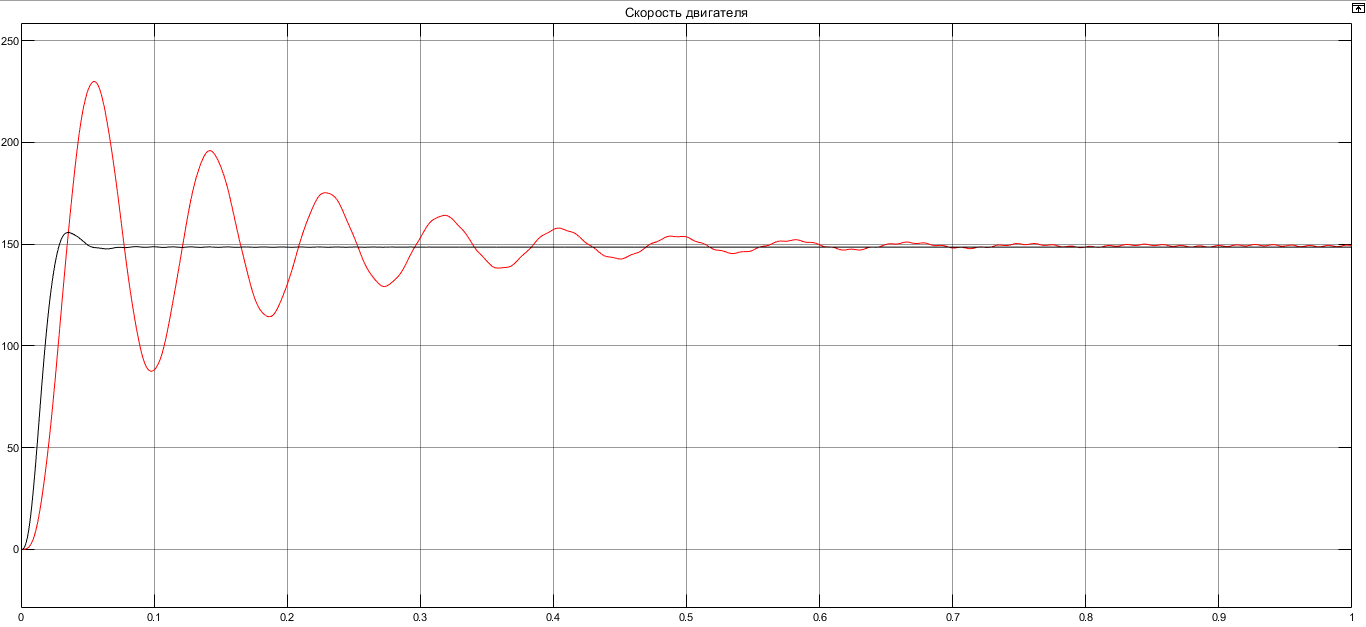 Рис. 4. Скорость двигателя 4) Сигнал по моменту на трубе: 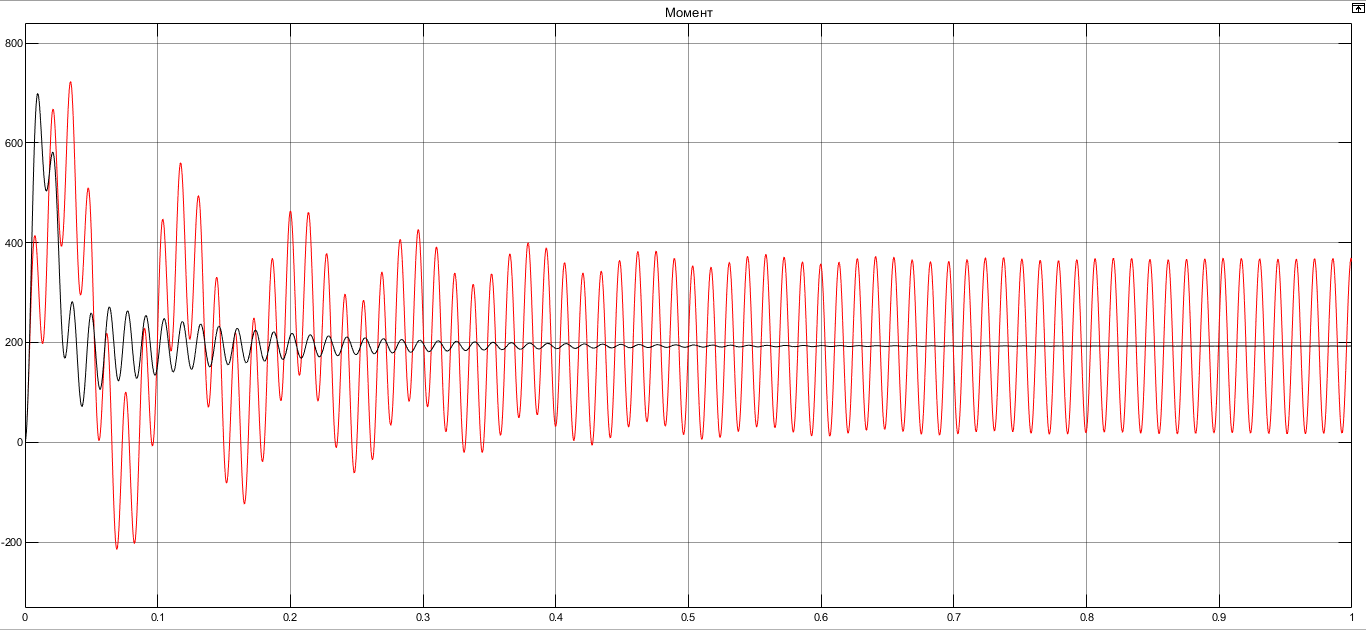 Рис. 5. Момент трубы 5) Сигнал скорости на нагрузке: 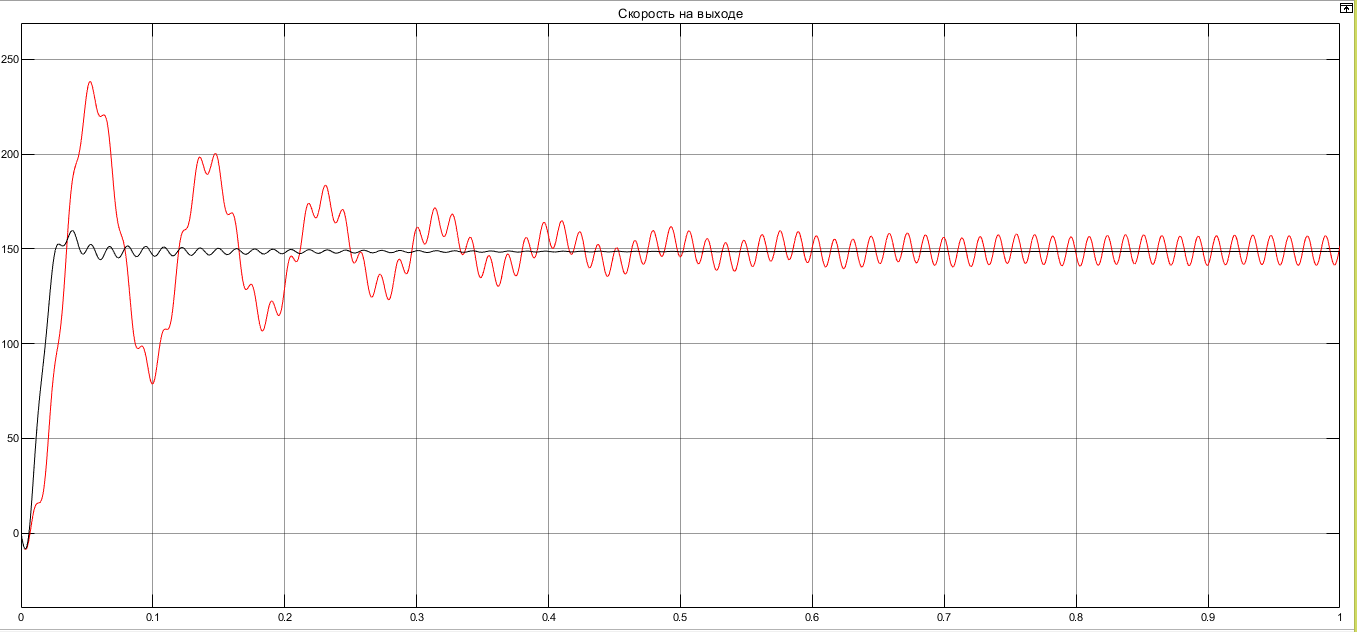 Рис. 6. Скорость на выходе Проведем оценку прямых показателей качества: Подчиненное регулирование Показатели качества: Установившееся рассогласование: 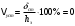 Перерегулирование: 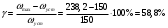 Время регулирования: 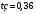 Колебательность: 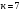 Модальный регулятор Установившееся рассогласование: 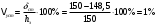 Перерегулирование: 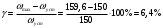 Время регулирования: 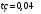 Колебательность:  II. Переходные процессы при 80% от номинальной нагрузке: 1) Сигнал на выходе с тиристорного преобразователя 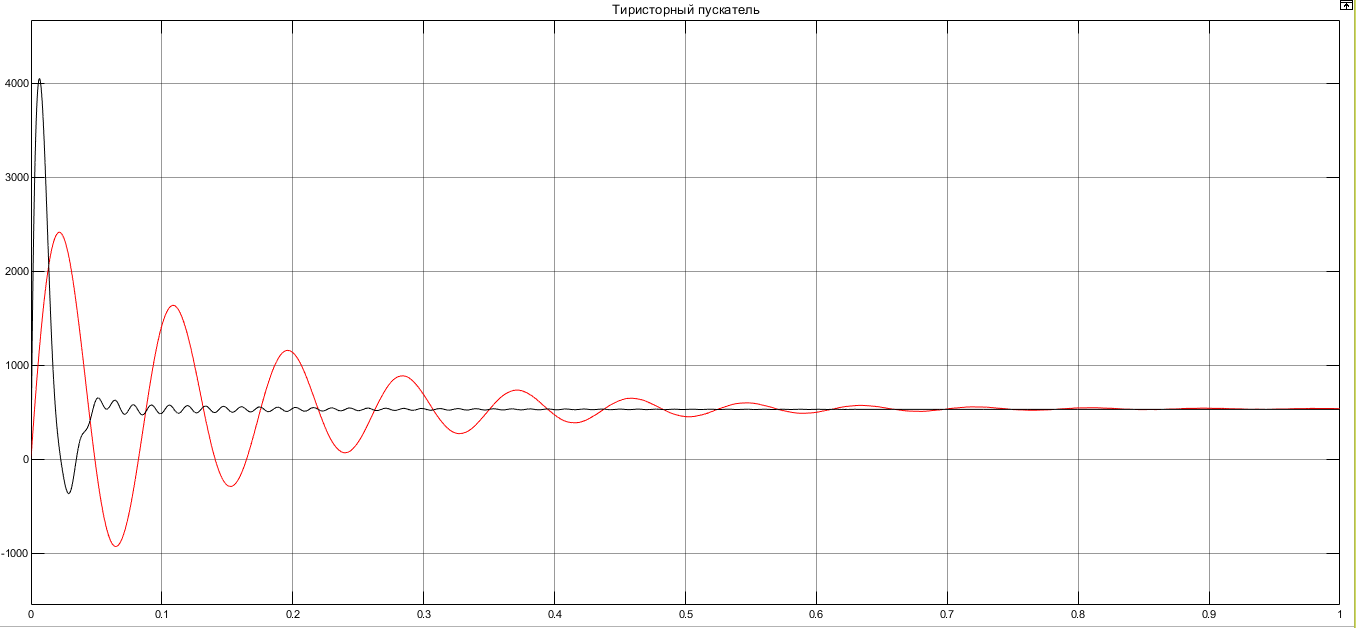 Рис. 7. Напряжение на тиристорном пускателе 2) Токи в двигателе: 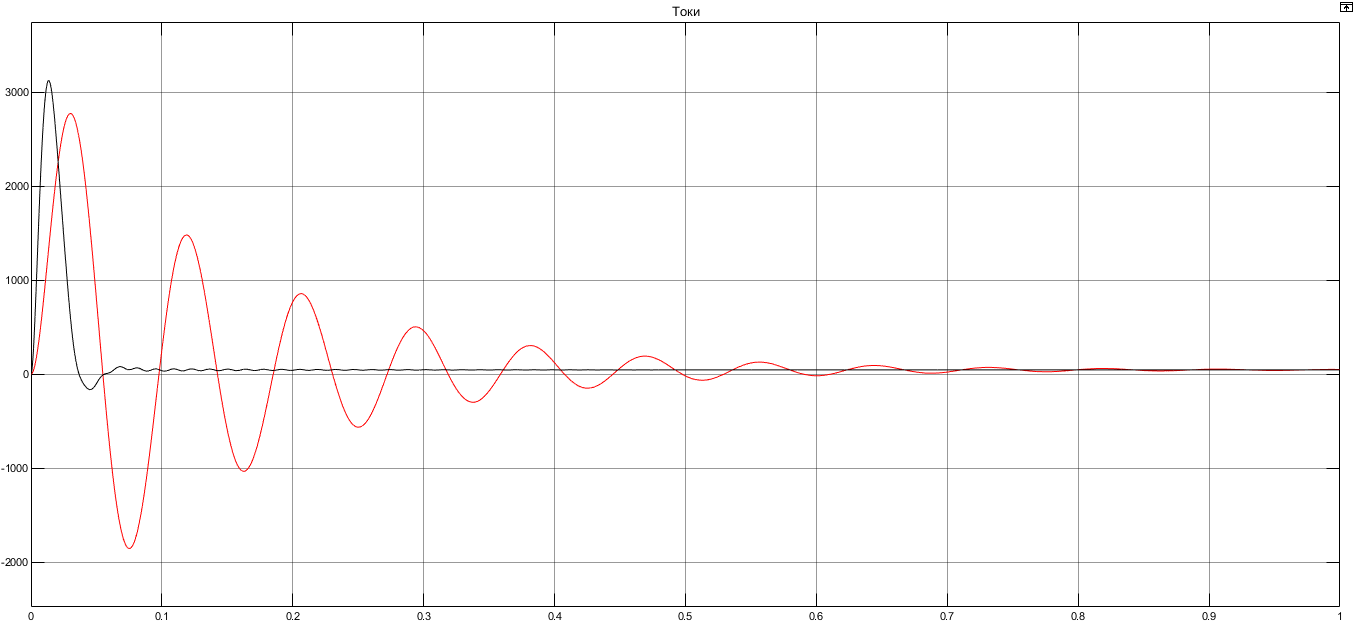 Рис. 8. Токи в обмотках двигателя 3) Сигнал по скорости на валу двигателя: 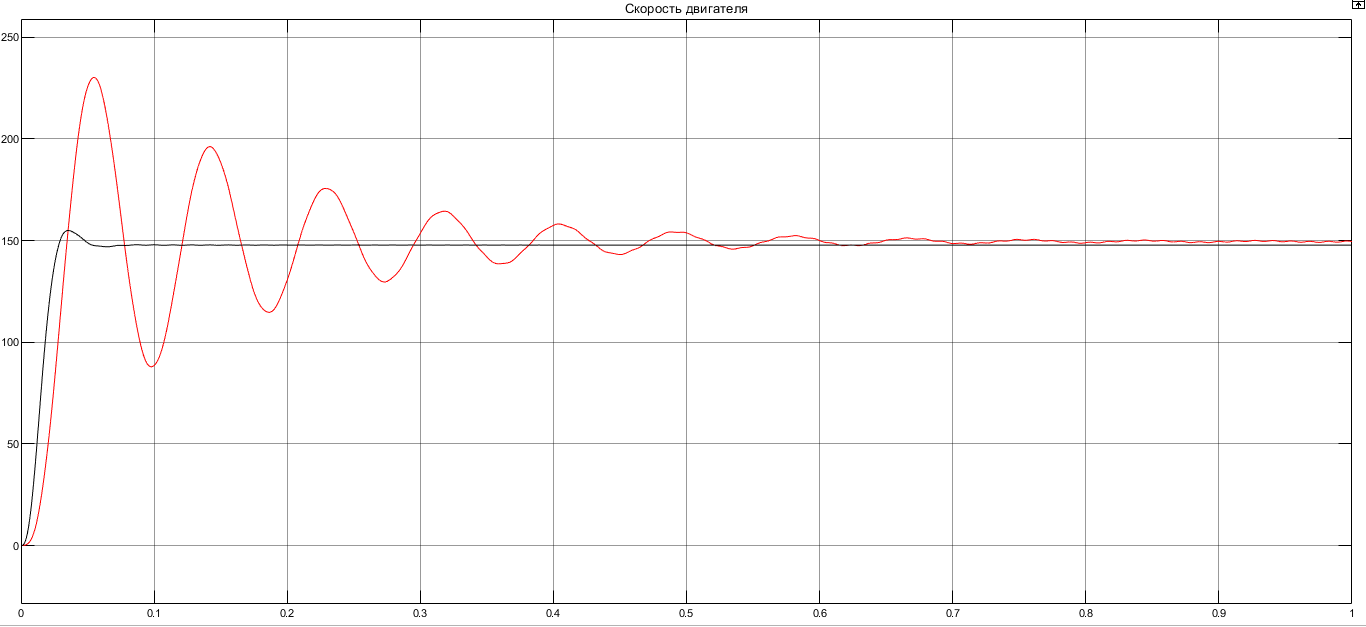 Рис. 9. Скорость двигателя 4) Сигнал по моменту на трубе: 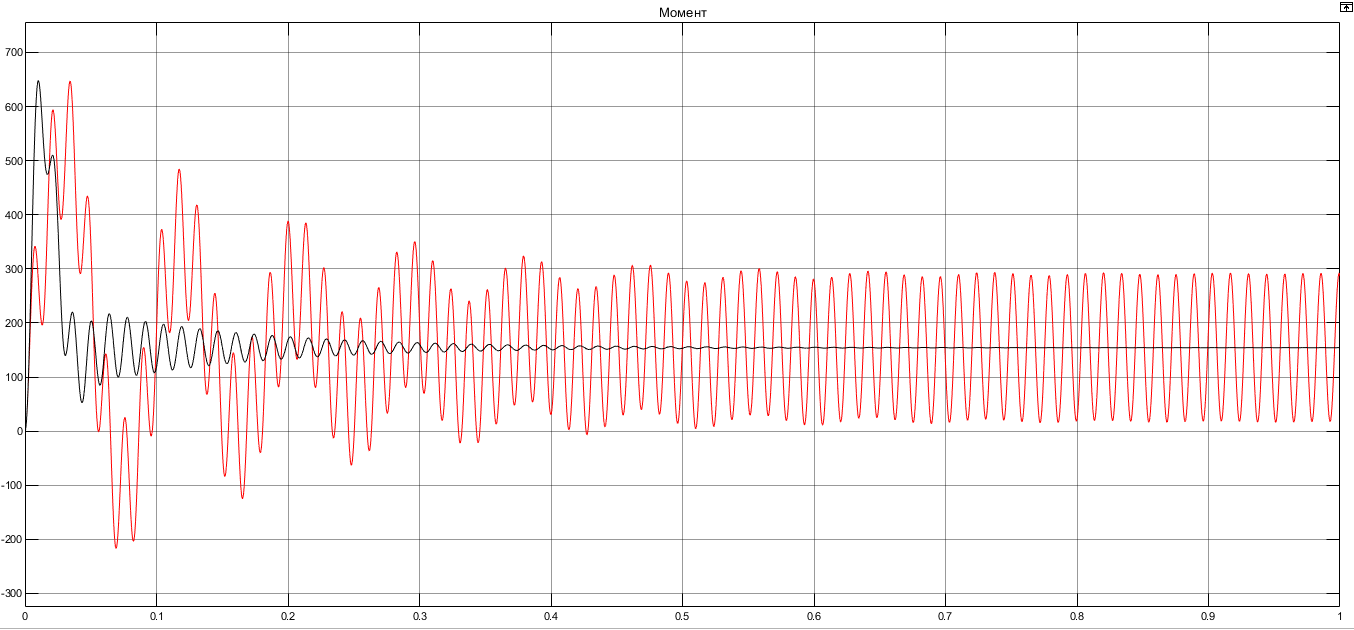 Рис. 10. Момент крутильной трубы 5) Сигнал скорости на нагрузке: 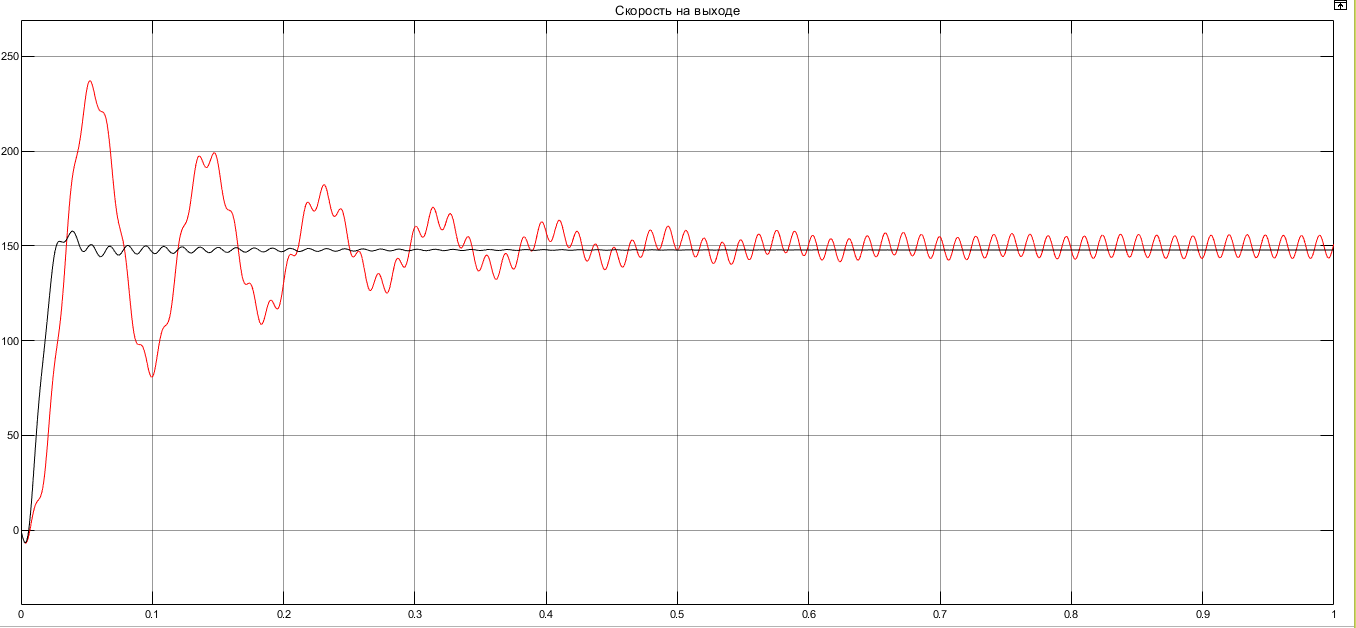 Рис. 11. Скорость на выходе Проведем оценку прямых показателей качества: Подчиненное регулирование Показатели качества: Установившееся рассогласование: 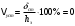 Перерегулирование: 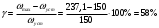 Время регулирования: 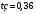 Колебательность: 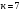 Модальный регулятор Установившееся рассогласование: 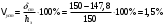 Перерегулирование: 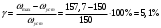 Время регулирования: 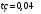 Колебательность: 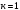 III. Переходные процессы при 150% от номинальной нагрузки: 1) Сигнал на выходе с тиристорного преобразователя 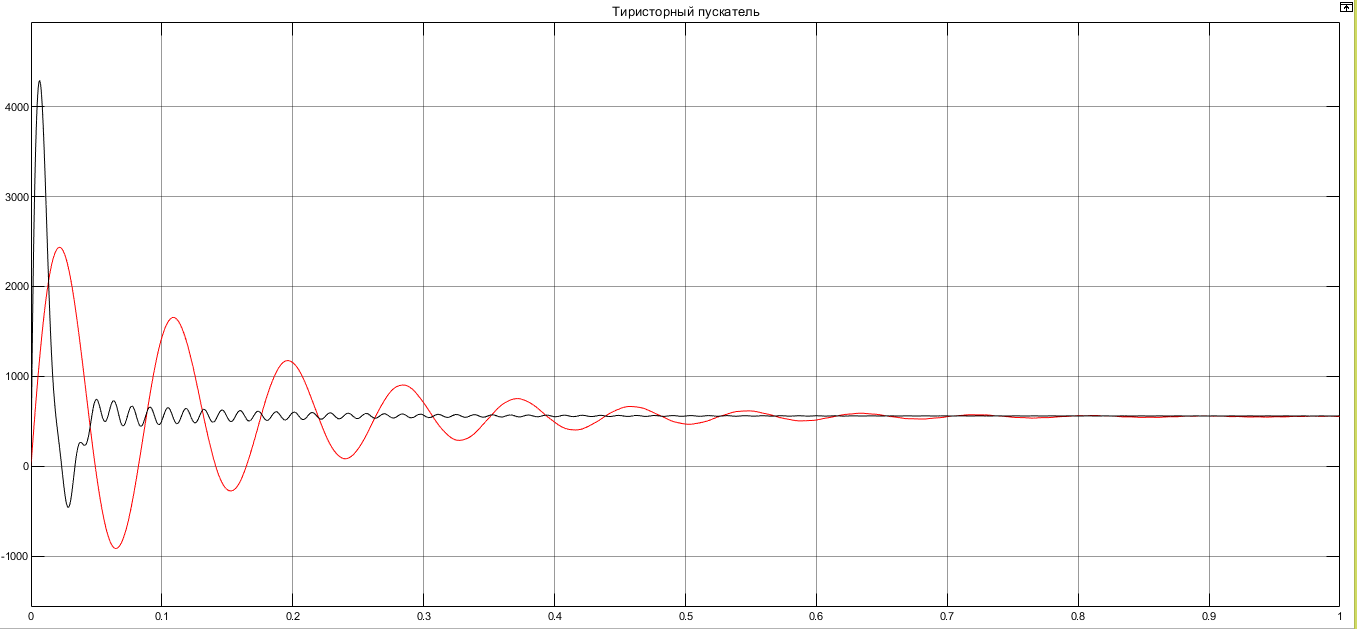 Рис. 12. Напряжение на тиристорном пускателе 2) Токи в двигателе: 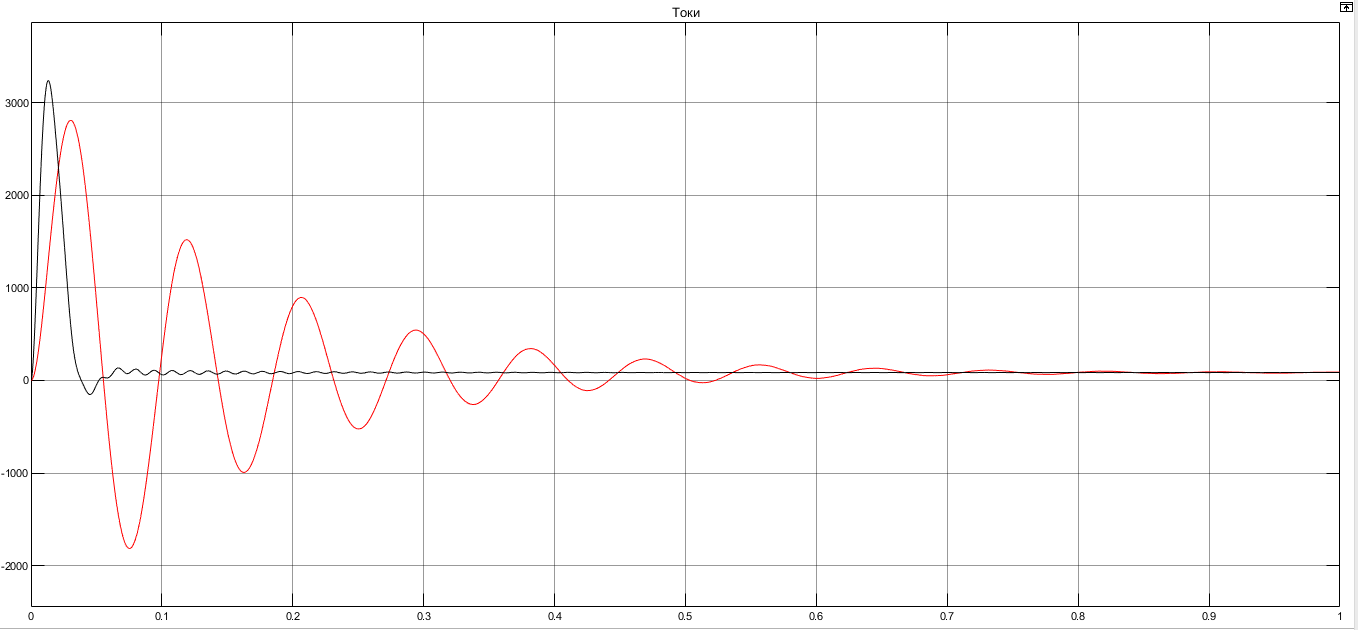 Рис. 13. Токи в обмотках двигателя 3) Сигнал по скорости на валу двигателя: 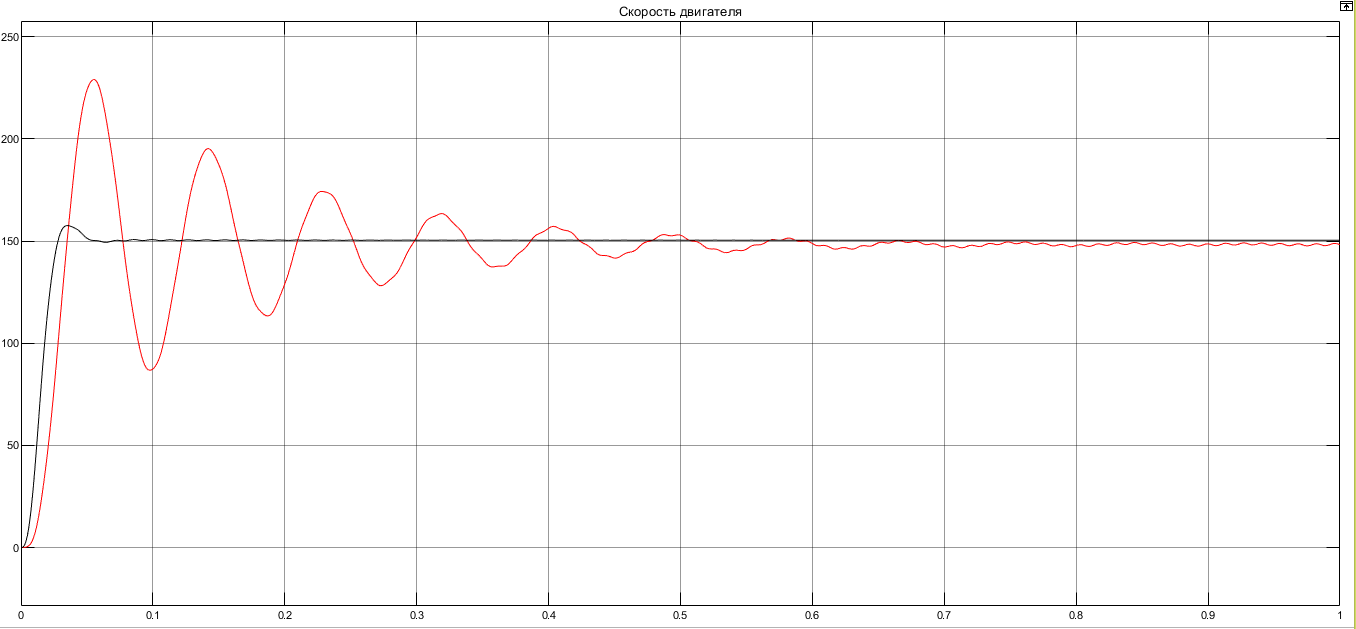 Рис. 14. Скорость двигателя 4) Сигнал по моменту на трубе: 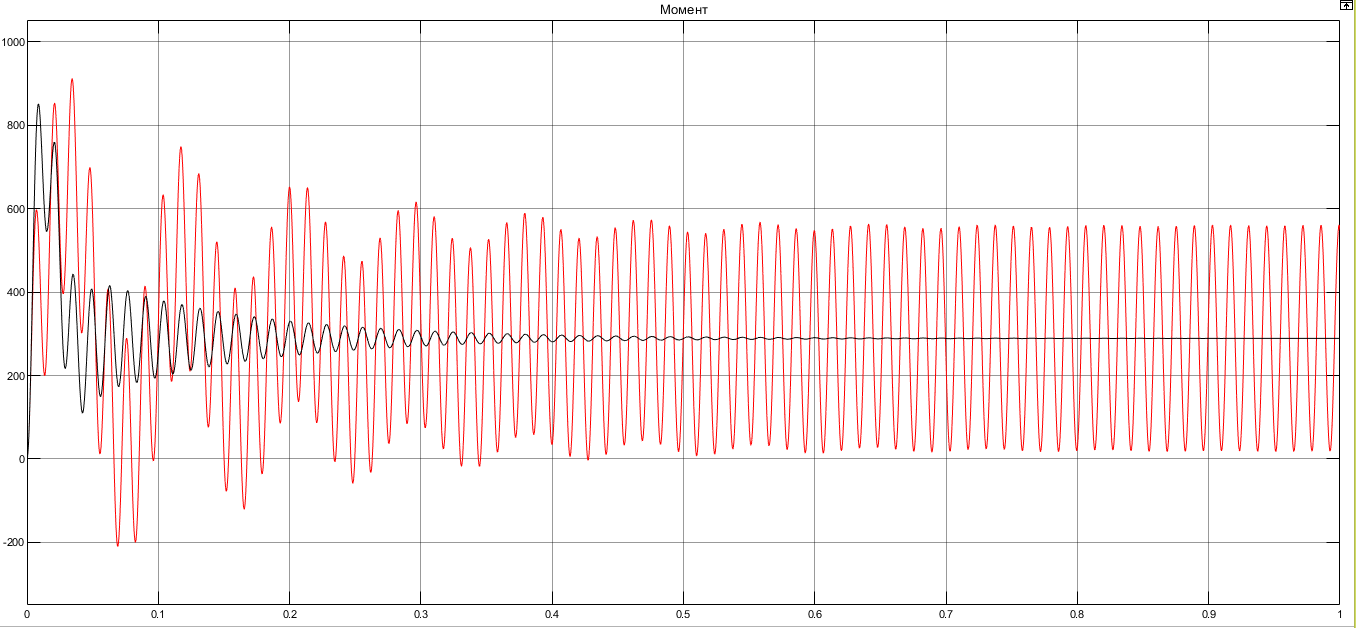 Рис. 15. Момент крутильной трубы 5) Сигнал скорости на нагрузке: 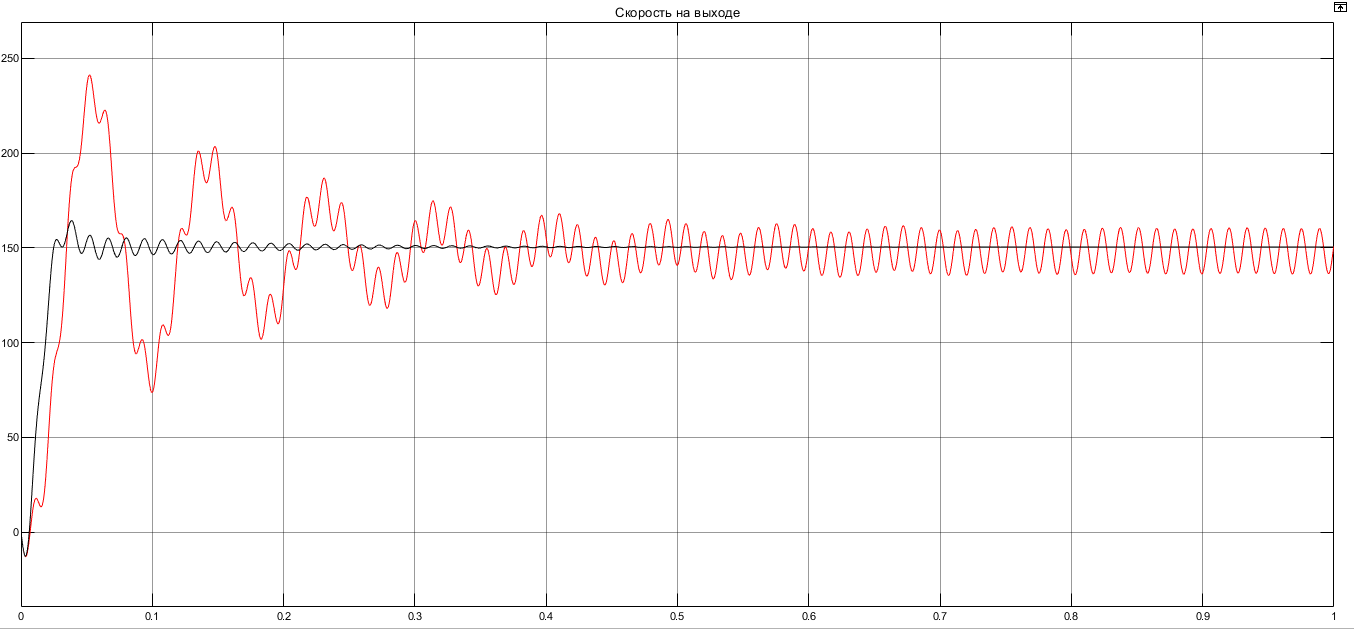 Рис. 16. Скорость на выходе Проведем оценку прямых показателей качества: Подчиненное регулирование Показатели качества: Установившееся рассогласование: 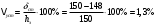 Перерегулирование: 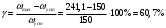 Время регулирования: 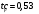 Колебательность: 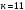 Модальный регулятор Установившееся рассогласование: 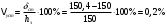 Перерегулирование: 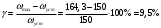 Время регулирования: 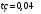 Колебательность: 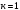 Проведем сравнение показателей качества двух систем Быстродействие: 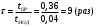 Перерегулирование 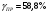 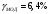 Вывод: в ходе лабораторной работы был осуществлен расчет модального регулятора для двигателя постоянного тока с двухмассовой нагрузкой. В качестве сравнения также рассматривалась система подчиненного регулирования. По мере выполнения работы видно, что модальный регулятор имеет преимущества и недостатки. На графиках тока и напряжения перерегулирование при использовании модального регулятора больше. Такие воздействия негативно будут сказываться на состоянии оборудования, или же придется выбрать варианты с большей износостойкостью. Это единственный замеченный недостаток. Первое преимущество модального регулятора в быстродействии. Второй в малом перерегулировании механических переменных как момент и скорость. Получается, что модальный регулятор имеет большое перерегулирование по току и напряжению и малое по моменту и скорости. Последнее важное замечание, что модальный регулятор подавляет гармонические составляющие в скорости и моменте в отличие от подчиненного регулирования. Санкт-Петербург 2021 | ||||||||||||||||||||||||||||||||