Следящая система

• Название: Следящая система
• Анкор: kursachtau
• Дата: 20.11.2021
• Размер: 1.43 Mb.
• Имя файла: kursovaya_TAU_1.doc
• Тип: Курсовой проект; #276816

Санкт-Петербургский

государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича

Кафедра АПС


Курсовой проект

Тема: “Следящая система “

Работу выполнил:

Работу проверила:
зав. каф. доцент Верхова Г.В.

ЧАСТЬ I

§1 Следящая система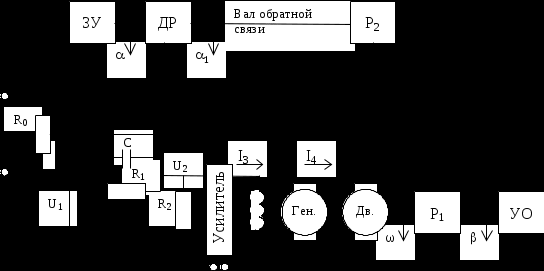


Рис. 1 Функциональная схема следящей системы.
ЗУ - задающее устройство

R₀ – потенциометр

Ген. - генератор

Дв - двигатель

Р₁, Р₂ - редукторы

УО - управляемый объект

ДР - датчик рассогласования

Краткое описание системы

Система предназначена для слежения в постоянном масштабе вала управляемого объекта за задающим валом. Механический дифференциал выполняет функцию датчика рассогласования сравнивая углы поворота вала задающего устройства  и вала обратной связи ₁, полученное рассогласование =-₁ с помощью потенциометра преобразуется в напряжение U₁, которое подается на вход дифференцируемого контура состоящего из емкости и сопротивлений R₁ и R₂. Усиленный усилителем ток I₃, поступает на обмотку возбуждающего генератора, цепь якоря которого последовательно соединена с цепью якоря двигателя постоянного тока с независимым возбуждением. Двигатель через редуктор Р₁ поворачивает вал управляемого объекта на угол =К₀*. Т.к. датчик рассогласования должен сравнивать величину одного масштаба в цепь обратной связи включен редуктор Р₂, задача которого изменение масштаба угла  в 1/К₀ раз.

ЧАСТЬ II

§1 Уравнения звеньев системы.

1. 
   Уравнение управляемого объекта с двигателем.
   

I – приведенный к валу объекта момент инерции всех масс, связанных с этим валом

М_вр – вращающий момент на валу объекта

М_Т – момент сил трения и сопротивления

М_НГ – момент внешней нагрузки на объект



I₄ – ток цепи якоря двигателя



– уравнение объекта с двигателем в стандартной форме

2. 
   Уравнение обратной связи.
   

3. 
   Уравнение датчика рассогласования.
   

4. 
   Уравнение потенциометра.
   

5. 
   Уравнение дифференцирующего контура.
   

Полезный сигнал дифференцирующего контура характеризуется правой частью уравнения, постоянная времени Т₂ определяет методическую ошибку при дифференцировании.

6. 
   Уравнение усилителя и цепи возбуждения генератора.
   

L₃ и R₃ – это индуктивность и сопротивление обмотки возбуждающего генератора

R_i – это внутреннее сопротивление лампы усилителя

I₃ – ток в цепи обмотки возбуждающего генератора

q – коэффициент усиления

В стандартной форме:

7. 
   Уравнение цепи якорей генератора и двигателя.
   

L₄, R₄ – индуктивность и сопротивление цепи якорей

I₄ – ток в цепи якорей

Е_Г – ЭДС генератора

Е_Д – противо ЭДС двигателя

считая, что (или с учетом уравнения редуктора )





Противо ЭДС двигателя играет роль дополнительной отрицательной обратной связи. Единое уравнение получено путем решения системы уравнений звеньев относительно рассогласования γ и задающего воздействия α.

При этом: ;

Система уравнений примет вид:

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   

Учитывая заданные параметры:



Получим:

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   
5. 
   
   
6. 
   
   
7. 
   
   

§2 Передаточные функции звеньев системы.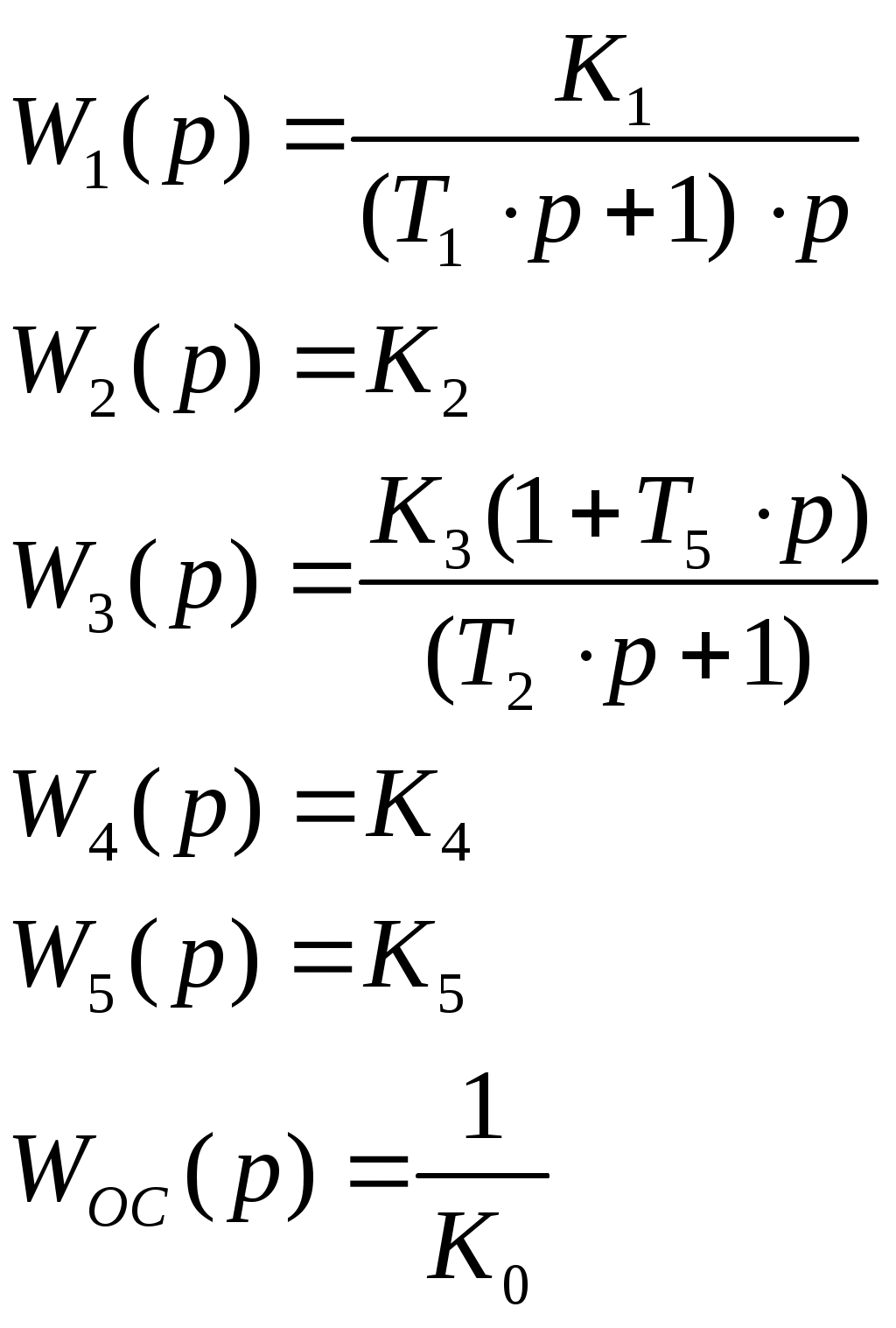



Так как в нашей следящей системе внешние воздействия отсутствуют, поэтому передаточные функции полностью отражают нашу систему.

Рис. 2. Структурная схема САУ.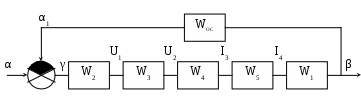
§3 Приведение системы уравнений по звеньям к
единому дифференциальному уравнению.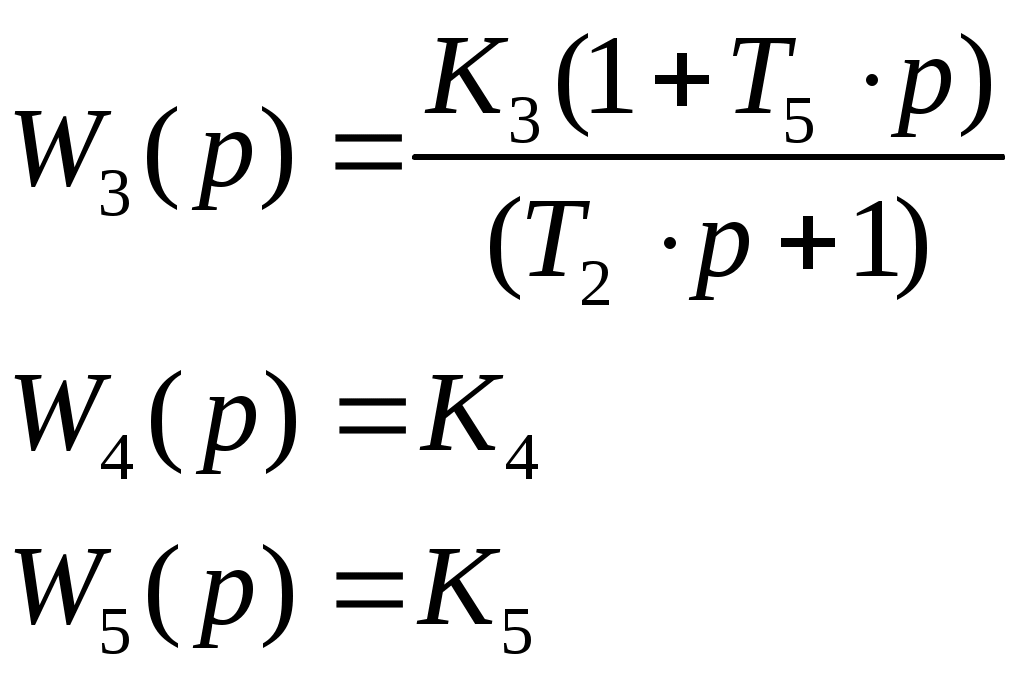





















Для того чтобы вывести единое уравнение, решим эти дифференциальные уравнения относительно рассогласования γ и задающего воздействия α.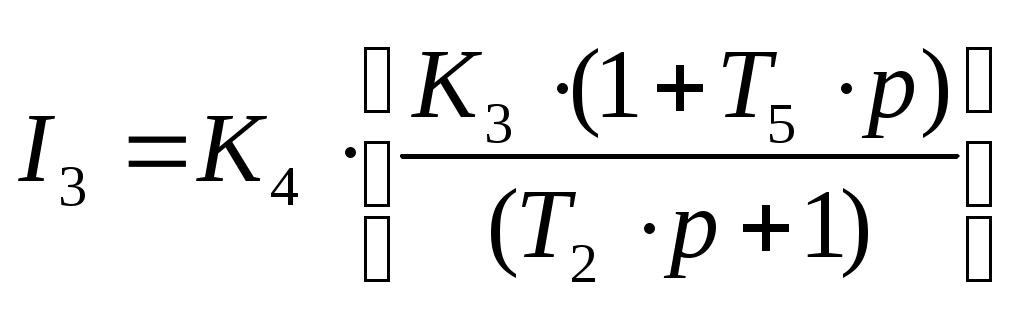









так как то





Единое уравнение системы:







Передаточная функция замкнутой системы и ее разомкнутой цепи: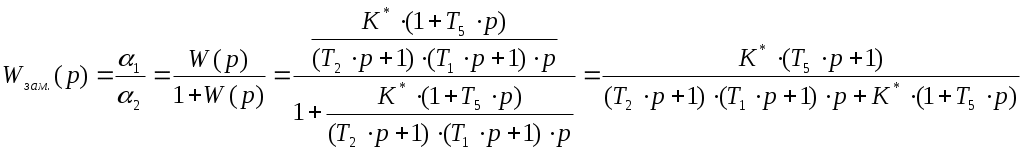



Передаточная функция по ошибке: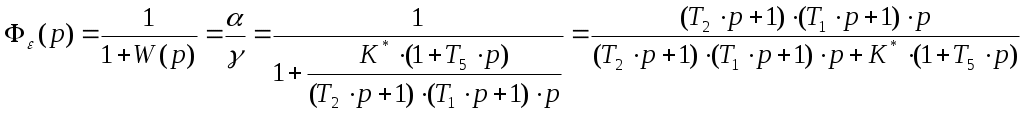



Передаточная функция разомкнутой цепи:



Часть III

§1 Получение уравнения статики системы и его использование при расчете системы.



γ – угол рассогласования входного и выходного вала.

α – угол поворота входного вала.

Искомыми параметрами являются коэффициент усиления К^* и Т₂ – постоянная времени дифференциального контура.

За статический режим следящей системы принимаем установившийся режим слежения за выходным валом, вращающимся с постоянной скоростью .

Подставив, получаем уравнение статики:





§2 Проверка системы на устойчивость.

Так как наша следящая система описывается уравнением третьего порядка, то для ее исследования на устойчивость удобно пользоваться критерием Вышнеградского, по которому для устойчивости линейной системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительны и произведение средних коэффициентов было бы больше произведения крайних.

Построение границы устойчивости.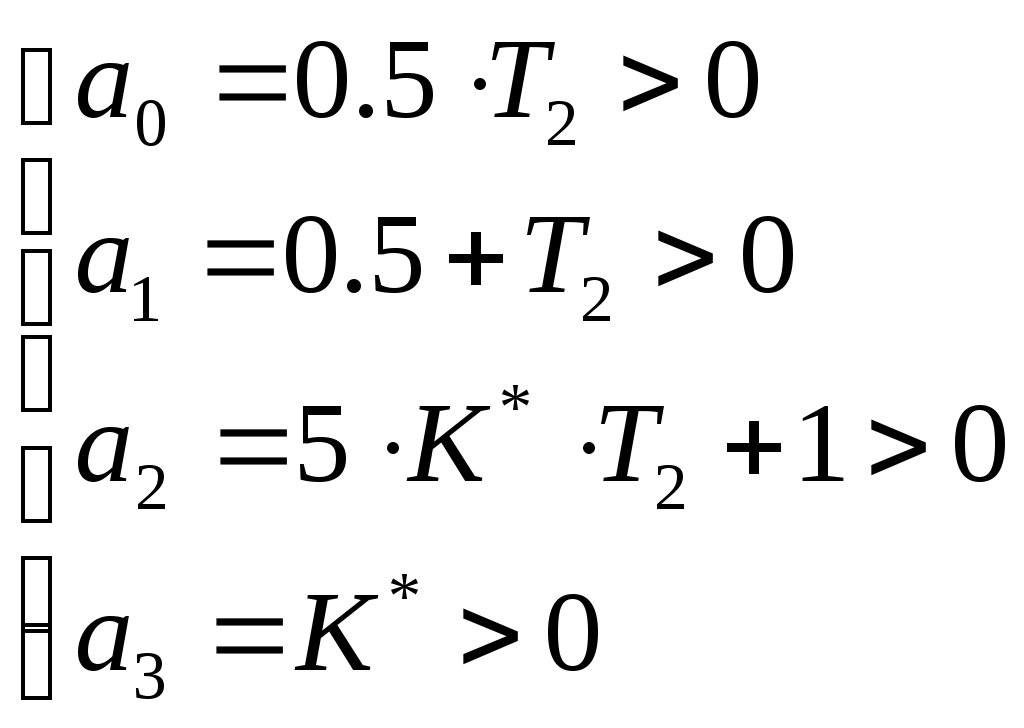







Система находится на границе устойчивости, если:





Построим график (рис. 3).

Т2	0.2	0.5	0.8	1	1.5	2	2.5	3	3.5	4	4.5	5	5.5
К*	-1.167	-0.444	-0.271	-0.214	-0.14	-0.104	-0.083	-0.069	-0.059	-0.051	-0.045	-0.041	-0.037

Пример расчета:





Если – система устойчива.

Если – система неустойчива.

Точка: А(0.2;-0.2)

Точка: В(1;-1)

Для точки А: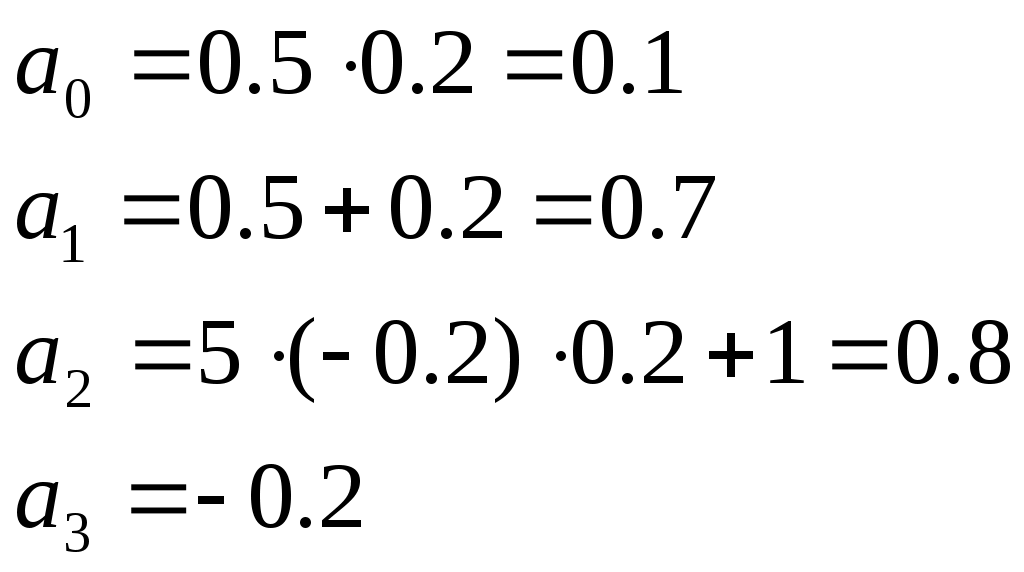



– система устойчива

Для точки В: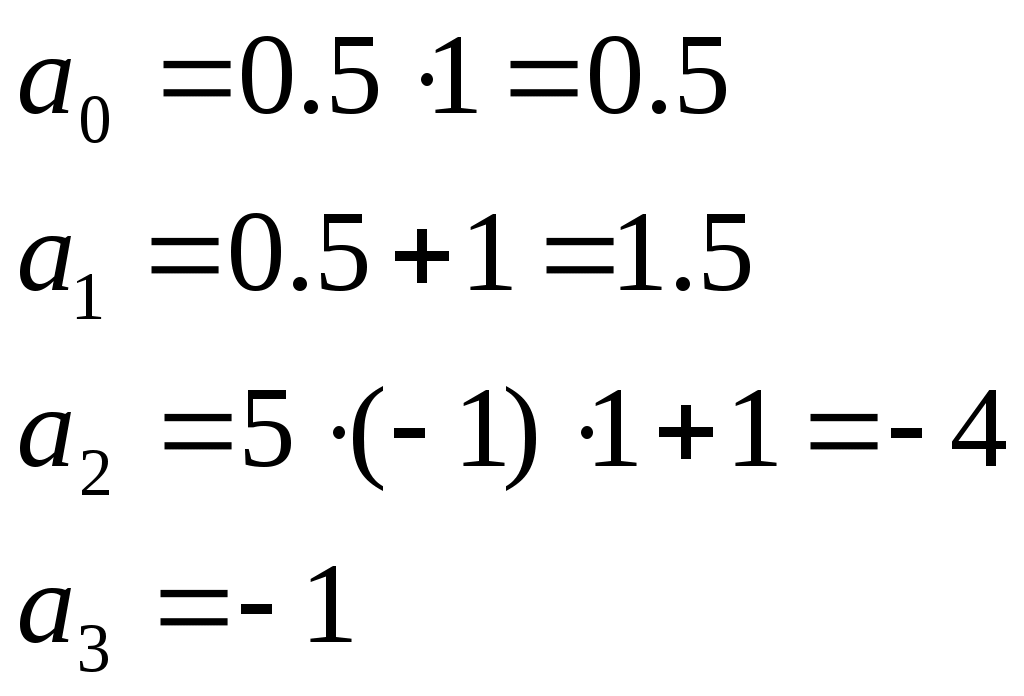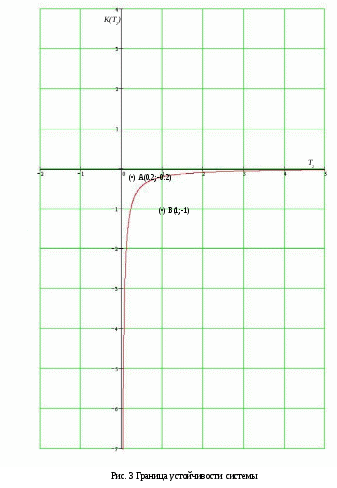



– система неустойчива



§3 Определение параметров системы по наибольшей степени устойчивости.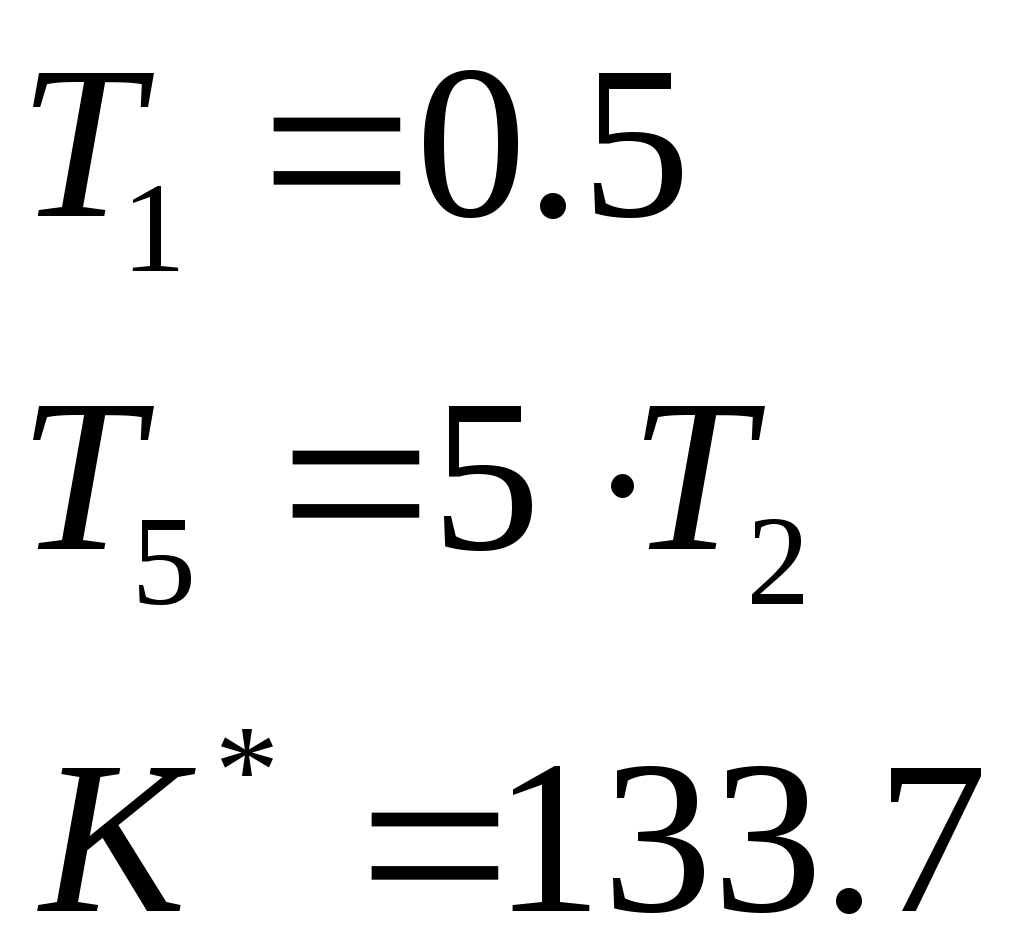



Нормальное уравнение:

Смещенное уравнение: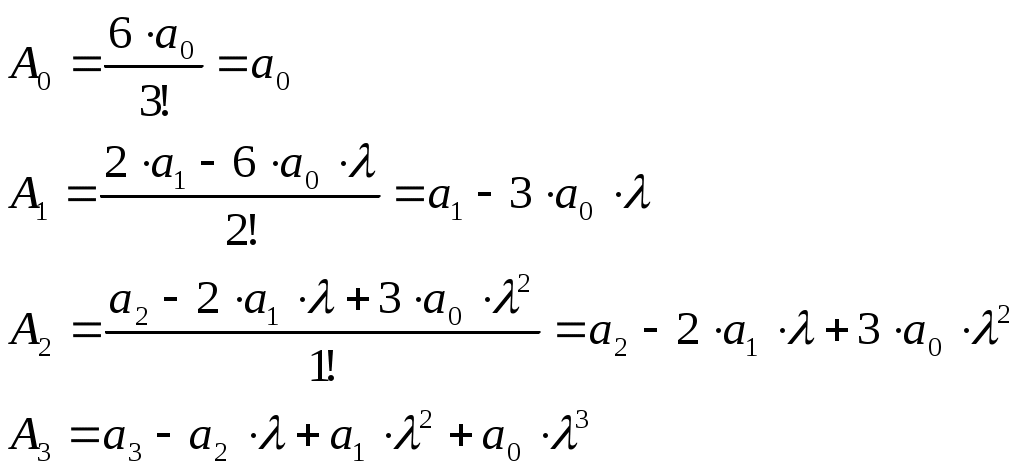





Так как смещенное уравнение 3-го порядка, поэтому воспользуемся критерием Вышнеградского, т.е. условием апериодической степени устойчивости, когда и условием колебательной степени устойчивости, когда

Для апериодической степени устойчивости:





Откуда находим h.

Построим график h(T₂) (рис. 4):

T2	0.01	0.015	0.02	0.025	0.03	0.04	0.05
h	87.985	44.693	15.254	9.689	7.454	5.252	4.103
T2	0.06	0.1	0.15	0.2	0.3	0.4	0.5
h	3.380	2	1.330	0.997	0.665	0.499	0.399

Пример расчета:



При уравнение для апериодической степени устойчивости имеет вид:

133.7-(133.75 +1)h+(0.5+ )h²-0.5 h³=0

Решением уравнения является .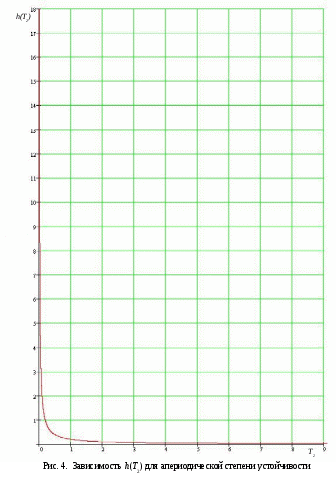




Аналогично для колебательной степени устойчивости:





Откуда находим h.

Построим график h(T₂) (рис. 5):

T2	0.01	0.015	0.02	0.025	0.03	0.04	0.05
h	7.007	11.987	18.373	16.556	13.940	10.874	8.949
T2	0.06	0.1	0.15	0.2	0.3	0.4	0.5
h	7.644	5.000	3.669	3.002	2.334	2.001	1.800

Пример расчета:

При уравнение для колебательной степени устойчивости имеет вид:



Решением его является h = 18.3.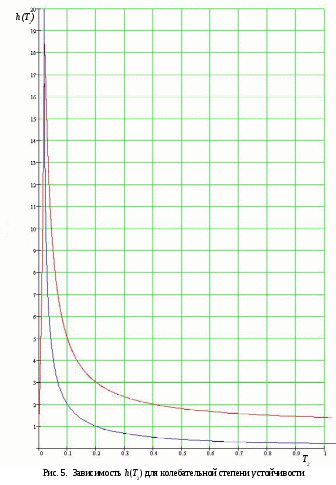




§4 Определение параметров линейной системы автоматического регулирования по наименьшей квадратичной оценке качества.

Если переходный процесс колебательный – то судить о качестве системы нужно с помощью квадратичной оценки.



где х – отклонение регулируемой величины от ее нового значения

Параметры системы, обеспечивающие минимум интеграла – оптимальны.

Пусть уравнение статической системы где задающее воздействие постоянно будет:



Отклонение регулируемой величины от ее нового установившегося значения в любой момент времени переходного процесса равно:



где x₁ – текущее значение регулируемой величины, отсчитываемое от ее старого установившегося состояния.

При единичной оценке при этих условиях А.А. Красновский предложил формулу:

, n>m

где Δ – определитель.

Δ_к составляется из: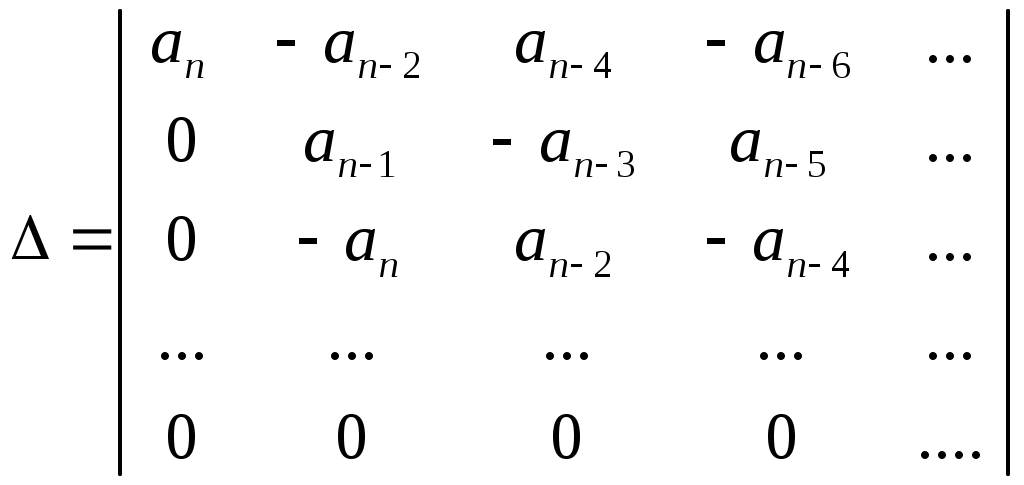



заменой столбца 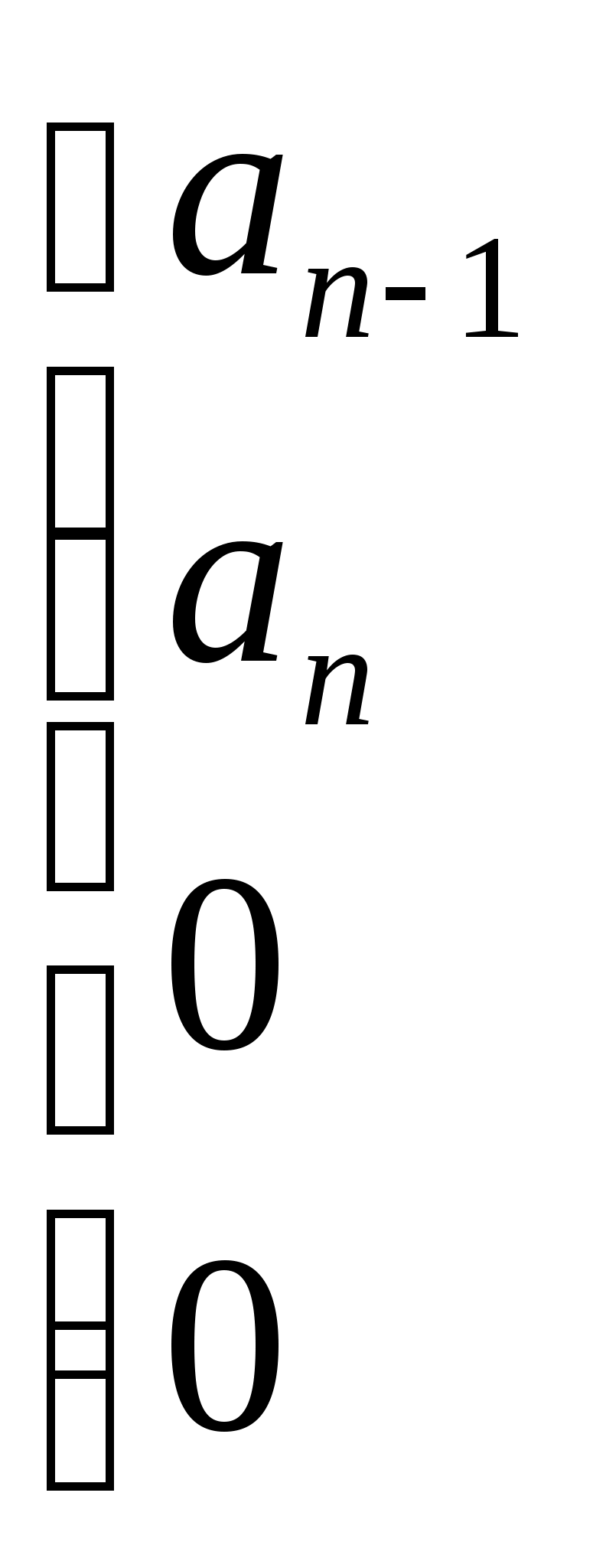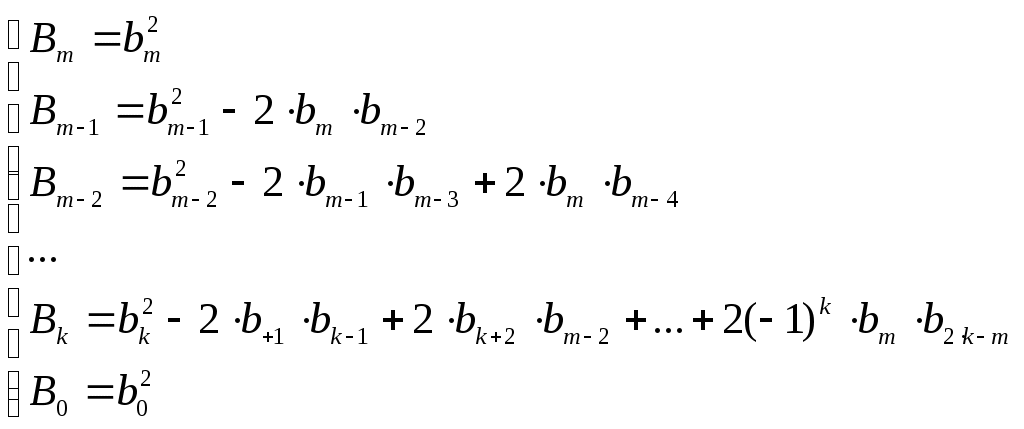столбцом



Отсюда: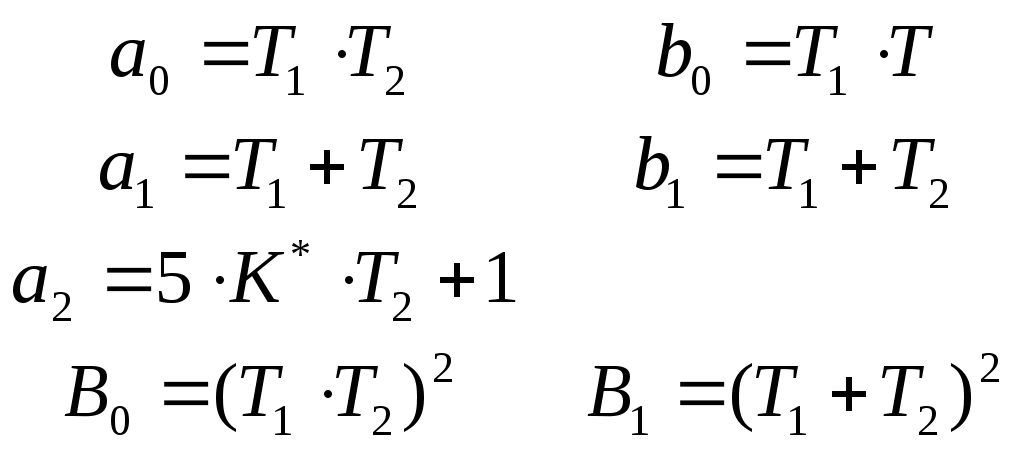

(1)



тогда: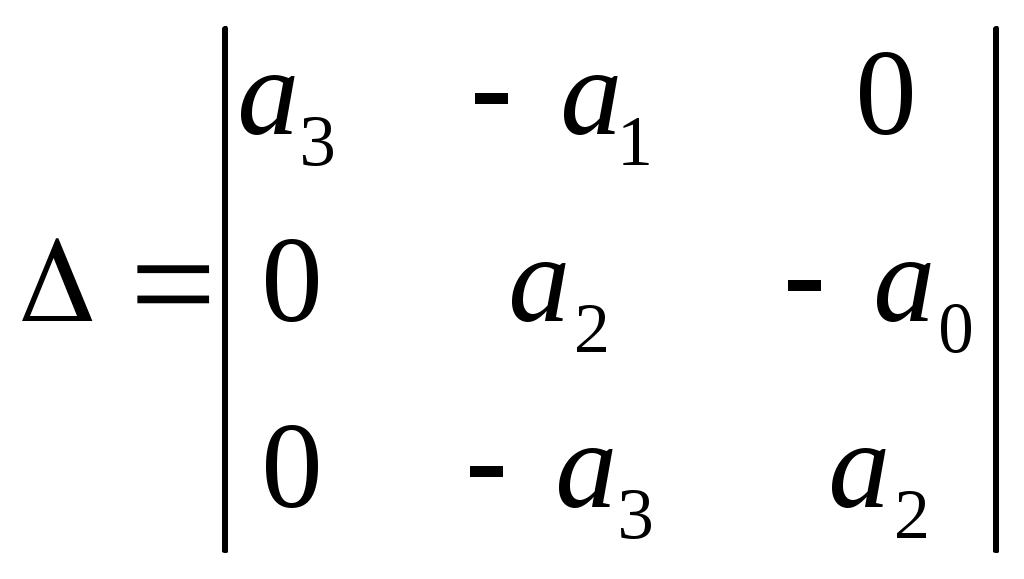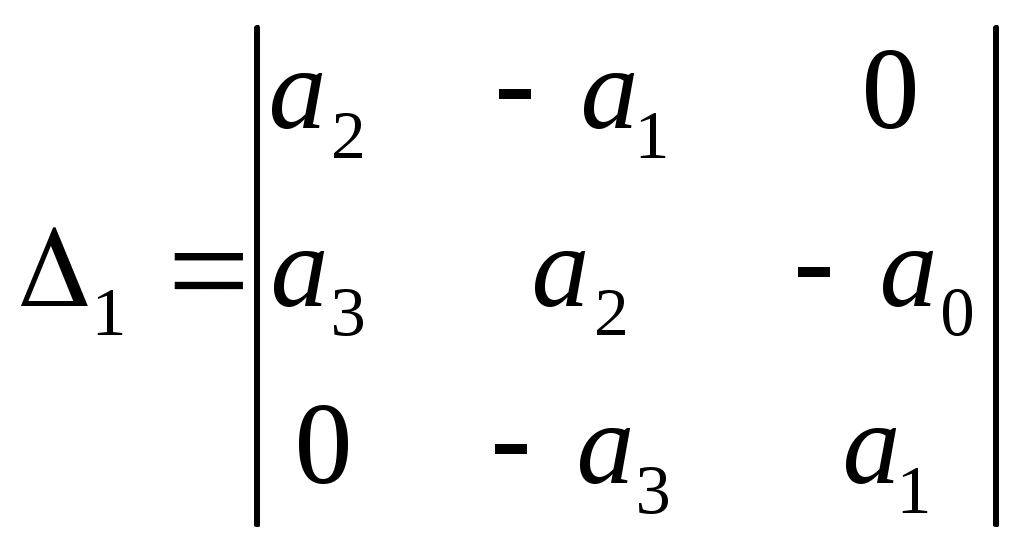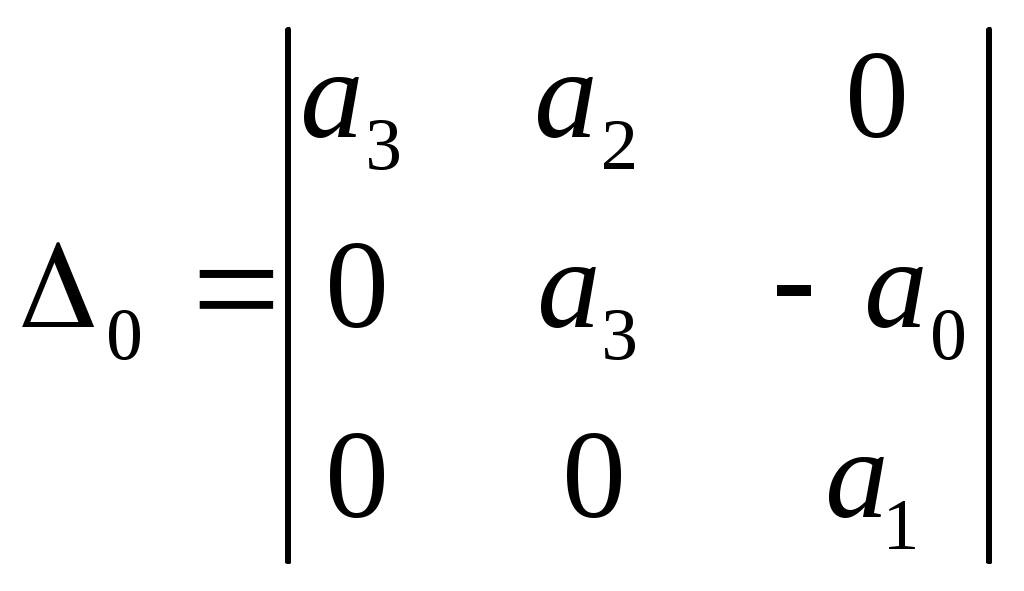



подставив в (1) получим: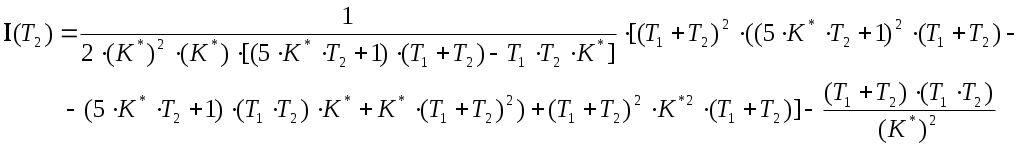



подставив К^*и Т₁ получим: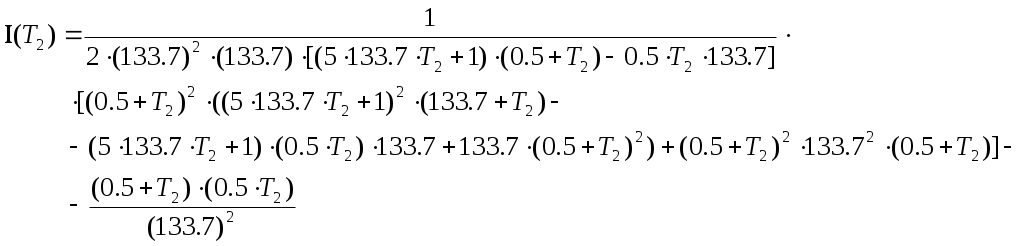



Отсюда узнаем, что будет при Т₂ = 0.0166

В результате этого расчета видно, что переходный процесс длится меньше по времени, чем переходный процесс в методе определения параметров по наибольшей степени устойчивости.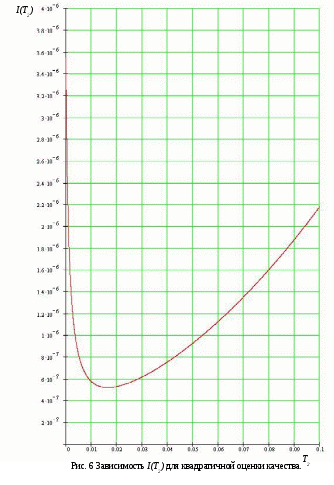




§5 Проверка САУ на устойчивость по методу Гурвица.

Чтобы САУ была устойчива необходимо и достаточно, чтобы все определители Гурвица имели одинаковые знаки со знаком первого коэффициента а₀ характеристического уравнения.



Т.е. при 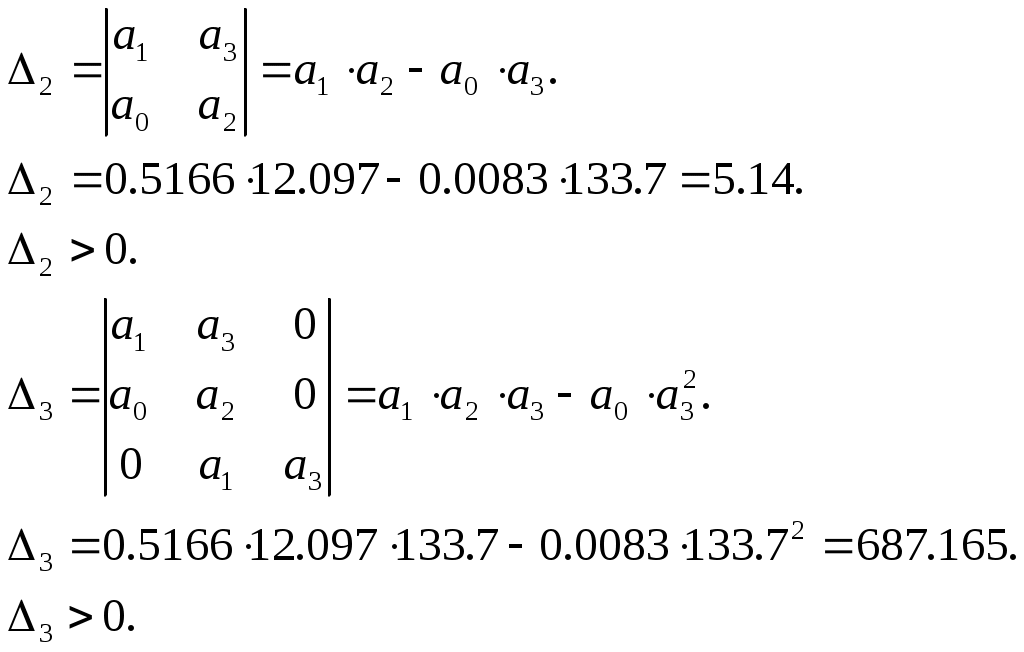были положительными.

а₁>0, а₂>0, а₃>0.



Т.о. Согласно критерию Гурвица САУ устойчива.

§6 Проверка САУ на устойчивость по методу Рауса.

Заполним табл. 4.

Коэффициенты таблицы определяем согласно формулам: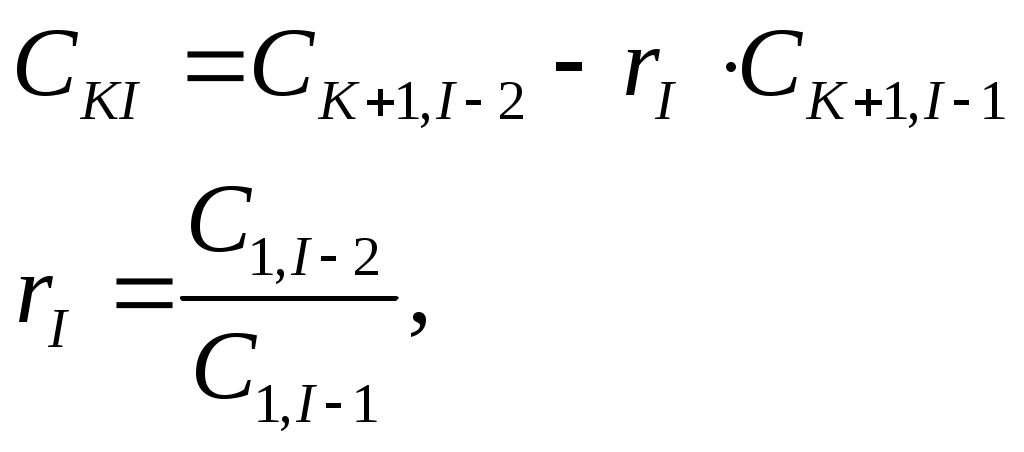



где К – номер столбца

I– номер строки

Табл.4 Таблица Рауса.

kn ri	Строки	столбцы
		1	2
---	1	C11=a0=0.0083	C21=a2=12.097
---	2	C12=a1=0.5166	C22=a3=133.7
r3 = 0.016	3	C13=a2-r3a3=9.958	C23=0
r4 = 1.025·10-3	4	C14=a3=133.7	C24=0

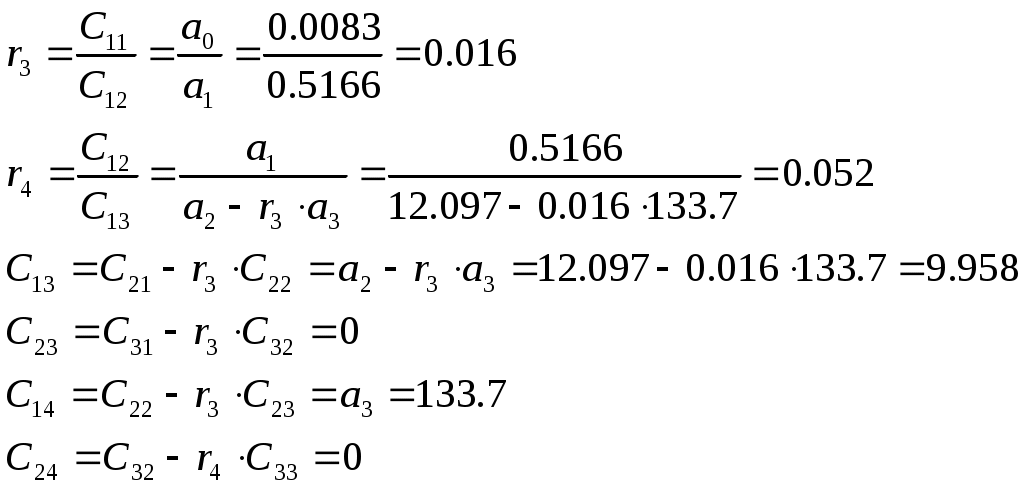Чтобы САУ была устойчива необходимо и достаточно, чтобы коэффициенты первого столбца таблицы имели тот же знак, что и а₀.

Т.к. а₀ > 0, то нужно, чтобы C₁₁>0, C₁₂>0, C₁₃>0, C₁₄>0.

Все коэффициенты первого столбца положительны, поэтому правых корней нет и, согласно критерию Рауса САУ – устойчива.

§7 Проверка САУ на устойчивость по методу Михайлова.

Характеристический полином:



Вещественная функция Михайлова:

Мнимая функция Михайлова:

САУ устойчива тогда и только тогда, когда X(ω) и Y(ω) имеют все действительные и перемежающиеся корни. Причем общее число этих корней равно трем, т.е. порядку характеристического уравнения. И при ω=0 удовлетворяют условию:



КорнемX(ω) является

Корнями Y(ω) являются , ω=0

Т.к. по определению ω>0, то корнями Y(ω) являются ω=38.177, ω=0.

Условия для ω>0 имеют вид



Все условия для критерия Михайлова выполняются, следовательно система является устойчивой.

Построим годограф Михайлова (рис. 7):

,рад/с	X()	jY()
0	133.7	0
10	82.1	108.96
16,097	0	154.02
20	-72.7	169.92
30	-33.7	134.88
38.236	-620.694	0
40	-691.9	-44.16
50	-1.156·103	-415.2
60	-1.724·103	-1.026·103
70	-2.395·103	-1.925·103

Т.к. годограф Михайлова, при изменении ω0 до ∞, начинаясь при ω=0 на вещественной положительной полуосиX(ω), обходит против часовой стрелки последовательно три квадранта координатной плоскости, то САУ по критерию Михайлова является устойчивой.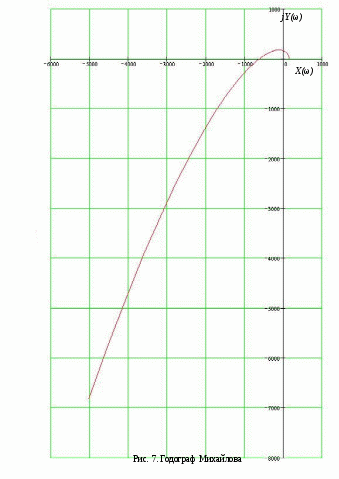



§8 проверка устойчивости САУ по критерию Найквиста.

Критерий Найквиста позволяет судить об устойчивости замкнутой системы по виду АФХ разомкнутой системы.

Передаточная функция разомкнутой цепи: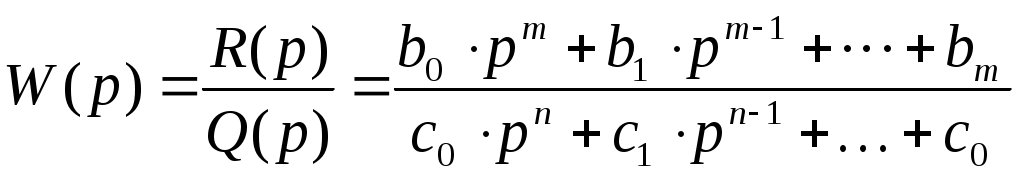




Будем считать, что b₃ = 1, тогда заменив p= j, частотная передаточная функция имеет вид: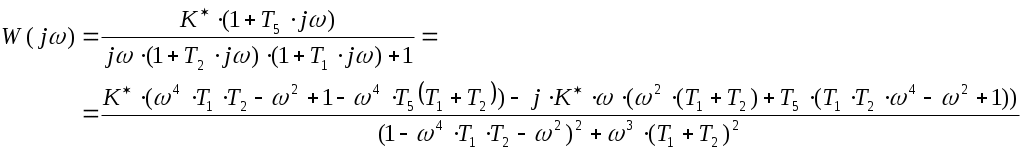



W(j) = U()+jV()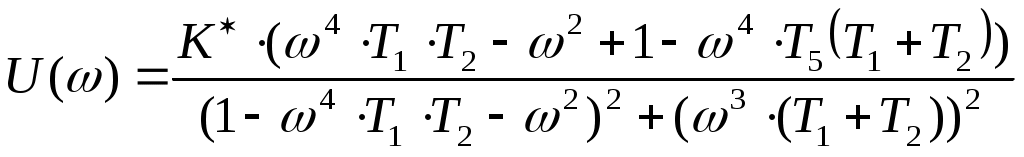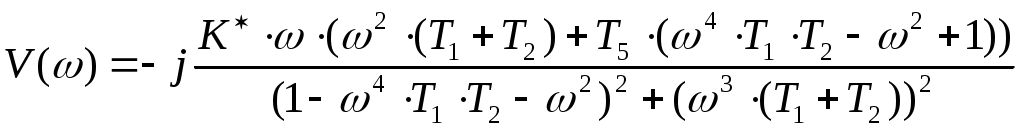





Построим годограф Найквиста (рис. 8):

,рад/с	U()	jV()
0	133,7	0
10	-0.198	-0.224
20	-0.04	-0.038
30	-0.015	-0.015
40	-7.46·10-3	-8.137·10-3
50	-4.101·10-3	-5.056·10-3
60	-2.434·10-3	-3.392·10-3
70	-1.528·10-3	-2.39·10-3
80	-1.002·10-3	-1.745·10-3
90	-6.806·10-4	-1.31·10-3
100	-4.768·10-4	-1.007·10-3
110	-3.428·10-4	-7.885·10-4

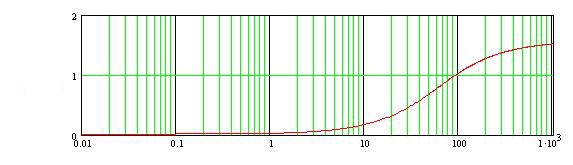
Пример расчета:

Если = 10, то: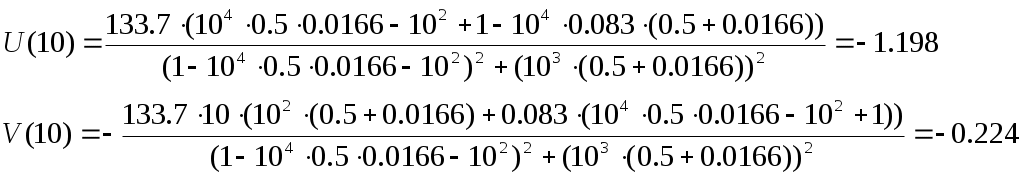



Из рис.6 видно, что годограф не охватывает точку (-1;j0), поэтому согласно критерию Найквиста замкнутая САУ – устойчива.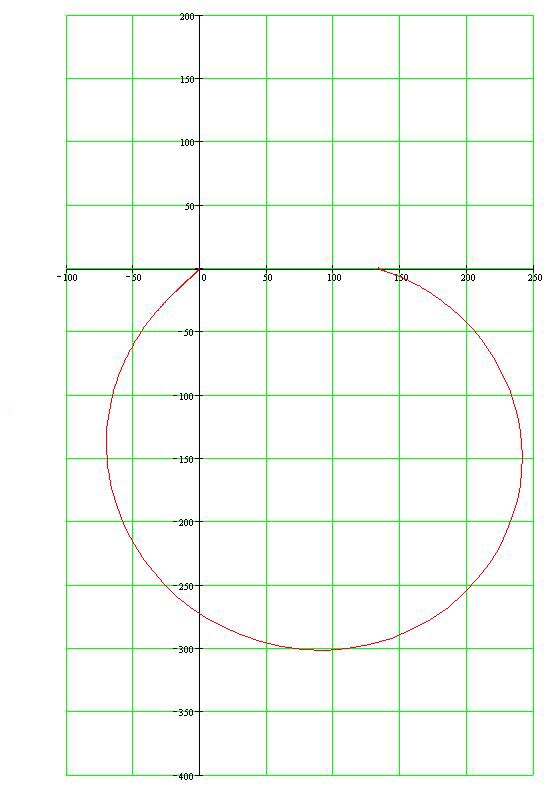



jV(ω)

U(ω)

Рис. 8. Годограф Найквиста

Часть IV

§1 Построение АФХ разомкнутой САУ

Частотная передаточная функция разомкнутой системы имеет вид: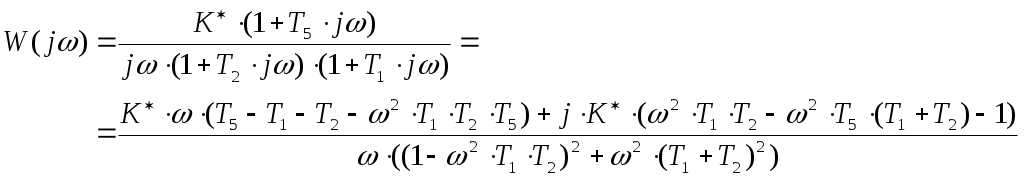



Её действительная часть: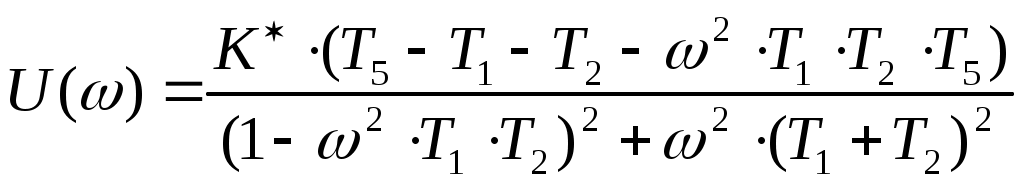



Её мнимая часть: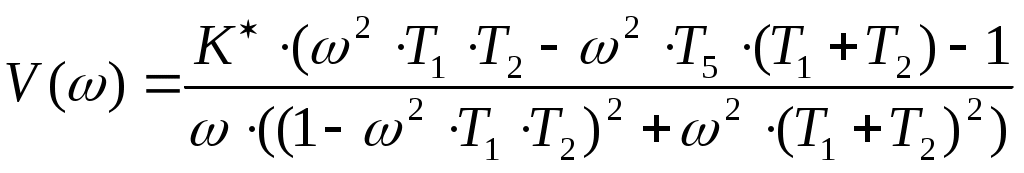



где

- АЧХ,

, где k= 0, 1, 2…- ФЧХ.

Построим АФХ системы (рис. 9):

,рад/с	U()	jV()
0	-57.972	-∞
10	-2.515	-2.231
20	-0.846	-0.884
30	-0.499	-0.508
40	-0.355	-0.326
50	-0.273	-0.221
60	-0.217	-0.156
70	-0.177	-0.113
80	-0.146	-0.084
90	-0.123	-0.064
100	-0.104	-0.049
110	-0.089	-0.039

угол запаса устойчивости. Найдём его, выбрав окружность единичного радиуса:

или =0,803рад.



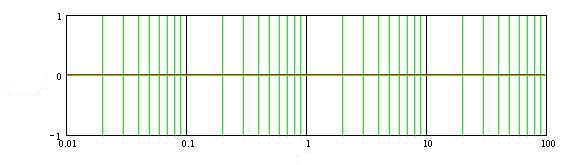
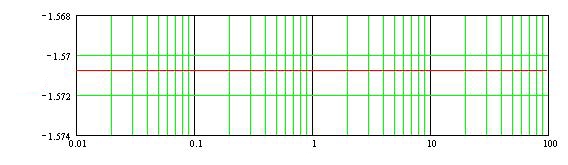
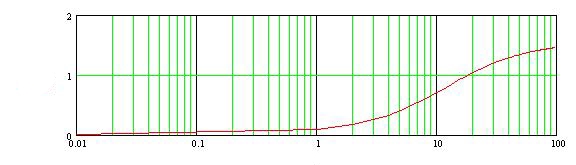
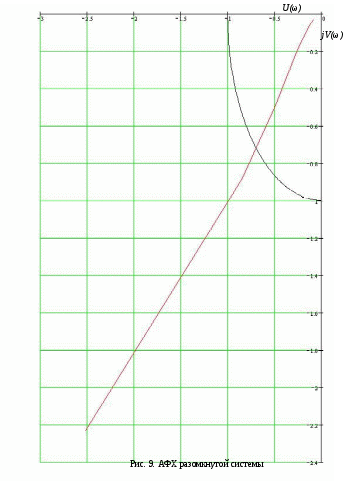§2 Построение ЛАЧХ и ЛФЧХ разомкнутой системы.

Передаточная функция разомкнутой системы: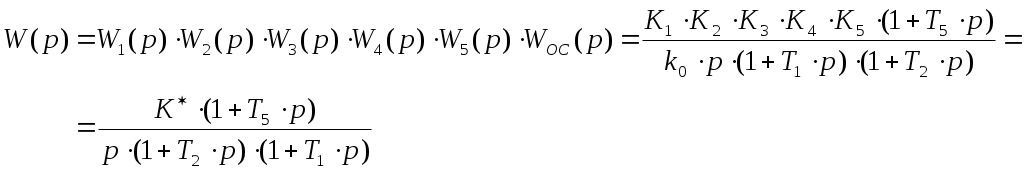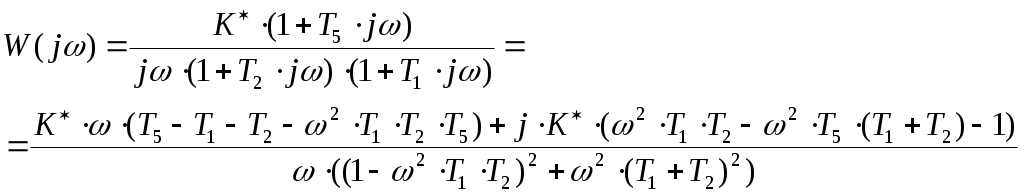





Cтроим ЛАЧХ и ЛФЧХ системы, как сумму ЛАЧХ и ЛФЧХ отдельных звеньев системы, т. е. AL=AL₁+AL₂+AL₃+AL₄+AL₅. Наша система состоит из 5 звеньев:

1 – усилительное звено(AL₁),

1 – интегрирующее звено(AL₅),

1 – форсирующее звено(AL₂),

2 – инерционных( AL₃, AL₄).
Т. о:




1). 0 , усилительное звено,

L() = 20lg(К^*) = 20lg(133.7) = 42.523(дБ)
2). (1/c)

1 инерционное звено,

L() = 20lg(133.7)+20lg ;
3).

форсирующее звено,

L() = 20lg(133.7)+20lg ;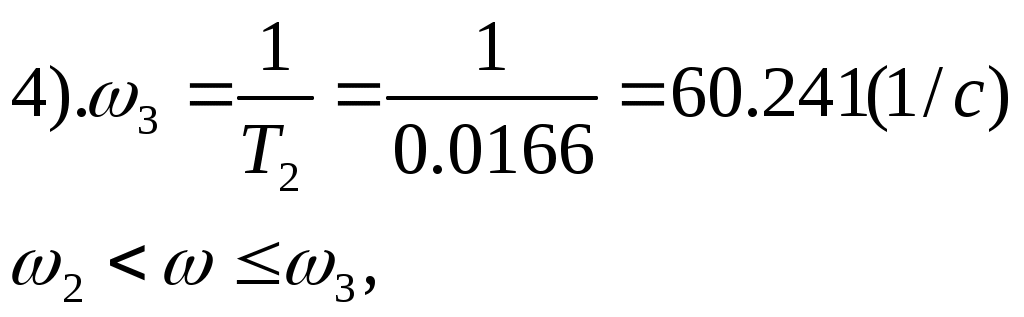


L() = 20lg(133,7) -20lg ; инерционное звено.

5). ₃, интегрирующее звено,



Строим ЛАЧХ системы (рис.10)
Построим ЛФЧХ системы для каждого звена в отдельности:


Таблица 8. ЛАЧХ и ЛФЧХ системы.

,1/с	L(),дБ
0,1	62.512
1	41.582
5	20.600
10	10.531
50	-9.092
100	-18.761
500	-45.496
1000	-57.492

Если = 10(1/с), то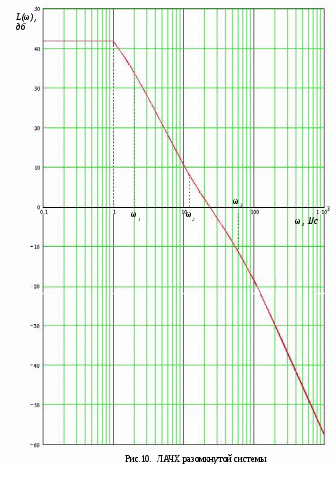



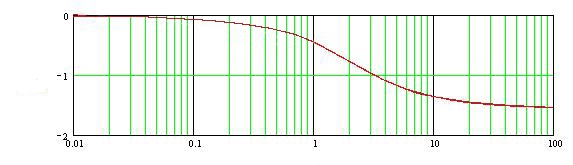
(рад).

	1 звено
	2 звено
	3 звено
	4 звено
	5 звено

Рис.11. ЛФЧХ звеньев системы

Часть V

Вывод

В данном курсовом проекте была исследована динамика следящей системы, из условия обеспечения допустимой скоростной ошибки ­_ст был найден общий коэффициент усиления САУ, а из условия обеспечения устойчивости было найдено значение Т₂ – постоянной времени дифференцирующего контура. Также САУ была исследована на устойчивость по критериям: Гурвица, Рауса, Михайлова, Найквиста. Были построены АФХ, ЛАЧХ, ЛФЧХ разомкнутой системы.