урок 7 класс Сложение и вычитание многочленов. сложение и вычитание многочленов. Сложение и вычитание многочленов
 Скачать 164.5 Kb. Скачать 164.5 Kb.
|
|
Тема: «Сложение и вычитание многочленов» Цель: формирование коммуникативных, личностных, регулятивных УУД. Задачи: - формировать знания о правилах сложения и вычитания многочленов и умения применять их в простейших ситуациях; - развивать умения сравнивать, выявлять закономерности, обобщать, делать выводы; - воспитывать ответственное отношение к учебному труду. Оборудование: таблица «Раскрытие скобок»; набор карточек для самостоятельного изучения темы; оценочные листы; карточки с кроссвордами; портреты математиков; карточки для устной работы; плакат с правилом заключения в скобки. Структура урока: Оргмомент. Постановка цели урока (2 мин.) Подготовка к изучению нового материала. (10 мин.) Ознакомление с новым материалом (15 - 20 мин.) Первичное осмысление и применение изученного (10 - 5 мин.) Подведение итогов урока(6 мин.) Постановка домашнего задания (2 мин.) Ход урока Постановка цели урока. Проверка подготовленности классного помещения к уроку. Сегодня мы продолжим изучать тему «Многочлены». Пока, вы только знаете определение многочлена, умеете, приводить многочлен к стандартному виду, и умеете определять степень многочлена. Далее нам предстоит рассмотреть вопрос о том, как складывать и вычитать многочлены. Запишите тему урока: «Сложение и вычитание многочленов». Подготовка к изучению нового материала. I. Для того чтобы вы могли успешно работать далее, повторим некоторые вопросы теории в ходе разгадывания кроссворда. 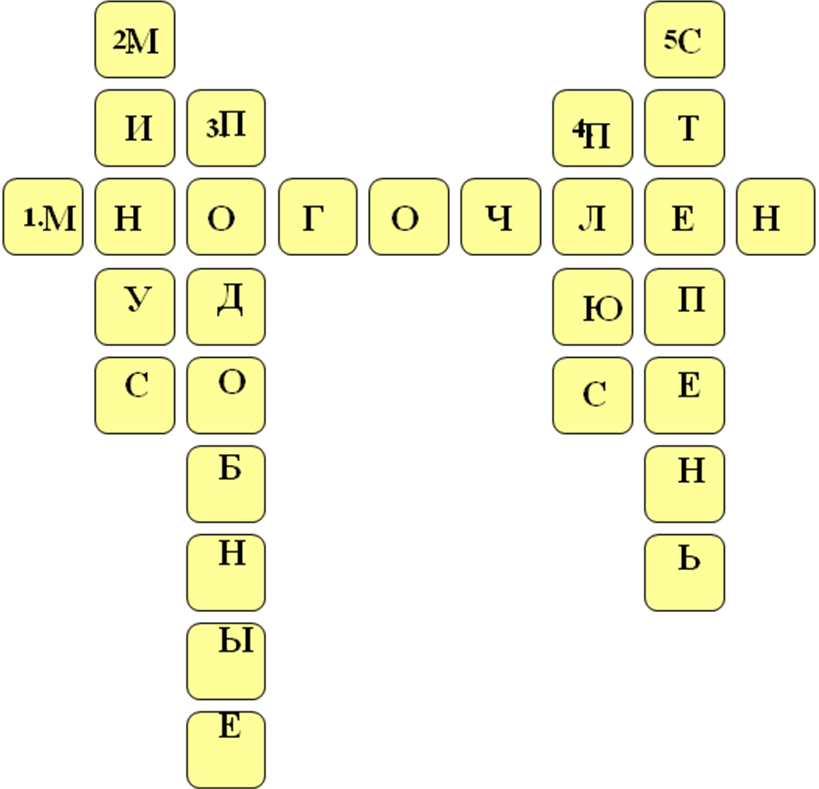 1. Сумма одночленов. 2. Знак разности. 3. Слагаемые многочлена, в которых коэффициенты различные, а буквенная часть одинаковая. 4. Знак суммы. 5. …многочлена стандартного вида – это наибольшая из степеней входящих в него одночленов. Взаимопроверка, выставление оценок. ------------------------------------------------------------------------ 6.Как раскрыть скобки, перед которыми стоит знак «+»? 7. Как раскрыть скобки, перед которыми стоит знак «-»? II. А теперь сосредоточьтесь и покажите, как вы владеете практическими навыками. Работаем устно. Устные упражнения: 1. Раскройте скобки: а) (х - у) + (- а + b); б) (а - b) – (с - d). 2. Приведите подобные члены многочлена: а) 45а – 12b + 16а; б) а3 – 3а + b + 2b – 2а3; в) 3. Ученик в процессе приведения подобных членов многочлена получил следующие результаты:
Учитель подчеркнул ответ и поставил знак вопроса, хотя подобные были приведены правильно. Почему был подчёркнут ответ? В каком виде его следует записать? Ознакомление с новым материалом Ребята, сейчас перед вами лежит огромная ответственность. Вам предстоит изучить новую тему, и от того, как вы поработаете, будут зависеть ваши дальнейшие успехи и успехи ваших товарищей. Внимательно изучите содержание лежащей перед вами карточки и выполните по образцу предложенное вам задание. Кому будет трудно, поднимите руку, я подойду и мы разберёмся вместе. После окончания работы над карточкой представитель от каждой группы выйдет к доске и объяснит остальным содержание своей карточки, а остальные учащиеся должны сделать соответствующие записи в тетради и по ходу объяснения задать вопросы, если возникнет необходимость. (учащиеся работают в группах по карточкам; учитель по необходимости помогает детям) Обучающая карточка №1 Тема: «Сложение и вычитание многочленов» Сложение многочленов Алгоритм действий: составить сумму многочленов; раскрыть скобки, перед которыми стоит знак «+»; привести подобные члены в полученном многочлене. Пример. Сложите многочлены 5х2 + 7х – 9 и – 3х2 – 6х + 8. (5х2 + 7х – 9) + (– 3х2 – 6х + 8) =5х2 + 7х – 9 – 3х2 – 6х + 8 = 2х2 + х – 1. Задание. Сложите многочлены: 2а3 – 5а + 5 и а3 – 4а – 2. Обучающая карточка №2 Тема: «Сложение и вычитание многочленов» Вычитание многочленов Алгоритм действий: 1) составить разность многочленов; раскрыть скобки, перед которыми стоит знак «-»; привести подобные члены в полученном многочлене. Пример. Выполните вычитание многочленов 5х2 - х +8 и 2х2 – 7х -1. (5х2 - х +8) - (2х2 – 7х -1) = 5х2 - х +8 - 2х2 + 7х +1 = 3х2 + 6х + 9. Задание. Выполните вычитание многочленов: 2а3 – 5а + 5 и а3 – 4а – 2. Обучающая карточка №3 Тема: «Сложение и вычитание многочленов» Представление многочлена в виде суммы многочленов (обратная задача) Правило: Чтобы заключить выражение в скобки, перед которыми требуется поставить знак «+», надо записать внутри скобок все члены выражения с теми же знаками. Пример. Представьте многочлен 5х3 – х2 – 7х + 2 в виде суммы, каких – ни будь двух двучленов. 1 сп. 5х3 – х2 – 7х + 2 = (5х3 – х2 ) + ( – 7х + 2). 2 сп. 5х3 – х2 – 7х + 2 = (– х2 – 7х) + (5х3 + 2). Задание. Представьте многочлен в виде суммы, каких – ни будь двух двучленов (любым, одним способом): х3 – 2х2 – 3х + 5. Обучающая карточка №4 Тема: «Сложение и вычитание многочленов» Представление многочлена в виде разности многочленов (обратная задача) Правило: Чтобы заключить выражение в скобки, перед которыми требуется поставить знак «-», надо записать внутри скобок все члены выражения с противоположными знаками. Пример. Представьте многочлен 5х3 – х2 – 7х + 2 в виде разности, каких – ни будь двух двучленов. 1 сп. 5х3 – х2 – 7х + 2 = (5х3 – х2 ) - ( 7х - 2). 2 сп. 5х3 – х2 – 7х + 2 = (– х2 + 2) - ( - 5х3 + 7х). Задание. Представьте многочлен в виде суммы, каких – ни будь двух двучленов (любым, одним способом): х3 – 2х2 – 3х + 5. Четыре ученика готовят необходимые записи на доске для объяснения нового материала и объясняют его. Самооценка. Выставление оценок. Первичное осмысление и применение изученного I. А сейчас я хочу проверить, как остальные ребята поняли своих товарищей. Четверо учащихся по очереди на доске выполняют задания: (остальные решают вместе с ними в тетради) Сложите многочлены: 2х2 + 3х и – х + 4. Выполните вычитание многочленов: 2х2 +3х и – х + 4. Представьте многочлен в виде суммы двух двучленов: 3а4 +2а3 + 5а2 – 4. Представьте многочлен в виде разности двух двучленов: – 5у4 +4у3 +3у2 – 2у. (остальные решают вместе с ними в тетради) II. Самостоятельная работа с самопроверкой. Выставление оценок. Вариант 1 - № 637 б); г). № 656 а). № 657 б). Вариант 2 - № 637 в); е). № 656 б). № 657 а). Подведение итогов урока I. Велика роль многочленов в математике. Многочлены являются довольно простыми функциями, которые легко дифференцировать и интегрировать. Теперь задумайтесь над таким фактом. Сложение, вычитание, умножение (умножение многочленов мы будем рассматривать несколько позже) всегда возможно, и результатом выполнения этих операций всегда будет многочлен. То есть, многочлены ведут себя как целые числа. В области многочленов работали такие известные математики как К.Ф.Гаусс – немецкий математик, Э.Безу – французский математик, П.Л.Чебышев. II. Выставление оценок из оценочного листа
Постановка домашнего задания Учитель комментирует домашнее задание: п.24. № 639 – на «3»; № 635 – на «4»; № 799 – на «5» |
