РАСЧЕТ ОГНЕСТОЙКОСТИ МЕТАЛЛИЧЕСКОЙ КОНСТРУКЦИИ. Содержание курсового проекта

• Название: Содержание курсового проекта
• Анкор: РАСЧЕТ ОГНЕСТОЙКОСТИ МЕТАЛЛИЧЕСКОЙ КОНСТРУКЦИИ
• Дата: 06.04.2023
• Размер: 1.66 Mb.
• Имя файла: Kursovaya_NV_Pozhar.docx
• Тип: Реферат; #1041899
• страница: 4 из 6

3.2 Теплотехнический расчет

Определим толщину сечения элементов фермы, приведенных к толщине пластины. Сечение элементов фермы

δ_пр = A / U,

где А – площадь поперечного сечения элемента фермы, м². В узлах фермы каждый элемент выполнен из двух уголков. Размеры уголка находятся в исходных данных.

U – длина обогреваемого периметра сечения элемента фермы, м;

U = 8b_f,

где b_f – ширина полки уголка, м.

Таким образом,

δ_пр = A / 8b_f, м;

δ_пр(P4)= A_(P4) / 8b_f(P4) = (2*10,6*10^-4)/(8*90*10^-3) = 2,9*10^-3 м;

δ_пр(С2)= A_(С2) / 8b_f(С2) = (2*8,63*10^-4)/(8*80*10^-3) = 2,7*10^-3 м;

δ_пр(Р5)= A_(Р5) / 8b_f(Р5) = (2*17,2*10^-4)/(8*110*10^-3) = 3,9*10^-3 м;

δ_пр(Н2)= A_(Н2) / 8b_f(Н2) = (2*28,9*10^-4)/(8*125*10^-3) = 5,8*10^-3 м;

δ_пр(Н3)= A_(Н3) / 8b_f(Н3) = (2*28,9*10^-4)/(8*125*10^-3) = 5,8*10^-3 м.

С использованием графиков изменения температуры нагрева незащищенных стальных пластин от времени нагрева и приведенной толщины металла при стандартном температурном режиме пожара (приложение 2, рисунок 6) определяем значения времени прогрева до критической температуры, то есть утраты их несущей способности (приложение 2, рисунок 6). Найденные значения сведем в таблицу 3.2.1.

Таблица 3.2.1.

Время прогрева до критической температуры элементов фермы

	Элемент фермы
	Р4	С2	Р5	Н2	Н3
Время прогрева до критической температуры t, мин	4	11	12	15	10

Вывод:

Фактический предел огнестойкости (Пф) принимают равным минимальному значению времени утраты несущей способности элементов фермы, то есть 4 мин (для элемента Р4).

4. РАСЧЕТ ФАКТИЧЕСКОГО ПРЕДЕЛА ОГНЕСТОЙКОСТИ ДЕРЕВЯННОЙ БАЛКИ ПОКРЫТИЯ

Фактический предел огнестойкости балки определяют по минимальному значению Пф, вычисленному из следующих трех расчетных условий.

Первое условие – потеря прочности по нормальным напряжениям.

Второе условие – потеря прочности по касательным напряжениям.

Третье условие – потеря устойчивости плоской формы (деформирования) изгибаемых конструкций, находящихся в условиях пожара, зависит не только от глубины обугливания (Z) древесины, но также и от возможного выхода из строя нагельных соединений элементов связей.
Расчет по условию потери прочности по нормальным напряжениям

Определять требования к балке по огнестойкости будем расчетным методом с учетом действующей на балку нормативной нагрузки.

Нормативная нагрузка на 1 погонный метр длины балки:

q_n = q* a_б / γ_f = 2,5* 6 / 1,2 = 12,5 кН/м.

В случае, если не известна длина балки, на которой произошло обрушение связей l_pc или l_pc = 0,5* L, M_lpc = ql²/8 то кНм, в противном случае M_lpc = (q_n/2)*(L/2-l_pc)*(L/2+l_pc) кНм.

Изгибающий момент от действия нормативной нагрузки в сечении балки, находящемся на расстоянии l_pc:

M_lpc = (q_n/2)*(L/2-l_pc)*(L/2+l_pc) = (12,5/2)*(12/2-3)*(12/2+3) = 168,75 кНм.

Поперечная сила от нормативной нагрузки:

Q_n = q_n ⋅ L / 2 = 12,5*12 / 2 = 75 кН.
Расчет по условию потери прочности по касательным напряжениям

От действия силы Q_n в опорных сечениях конструкции возникают максимальные касательные напряжения.

Коэффициент изменения прочности по нормальным напряжениям:

η_w = M_lpc / (W*R_fw) = 168,75* 10³ / (22,44* 10^-3 *29* 10⁶) = 0,26,

где W – момент сопротивления для прямоугольного сечения, равный:

W = В_б *h² / 6 = 170* 890² / 6 = 22,44*10^-3 м³;

R_fw – расчетное сопротивление древесины изгибу при нагреве, МПа.

Определим критическую глубину обугливания, при достижении которой наступает предельное состояние конструкции по огнестойкости (σ_n = R_fw), при действии нормальных напряжений.

По номограмме (приложение 2, рисунок 7) для числа обогреваемых сторон 3,

h / В_б = 890/170 = 5,24 и η_w = 0,26 определяем, что:

Z_crw = 0,25*В_б = 0,25* 170 = 42,5 мм (так как найденная точка лежит ниже штрихпунктирной линии).

Коэффициент изменения прочности по касательным напряжениям:

η_a = 3Q_n / (2B_б h*R_fqs) = 3* 75* 10³ / (2* 170* 10^-3* 890* 10^-3* 1,2* 10⁶) = 0,62;

где R_fqs – расчетное сопротивление древесины скалыванию, МПа.

Определим критическую глубину обугливания, при достижении которой наступает предельное состояние конструкции по огнестойкости (σ_n = R_fw), при действии касательных напряжений.

По номограмме (приложение 2, рисунок 7) для числа обогреваемых сторон 4.

h/В_б = 890/170 = 5,24 и η_a = 0,62 определяем, что

Z_cra = 0,027*890 = 24,03 мм.

Из двух значений Z_crw и Z_cra, выбираем наименьшее, таким образом

Z_cr = 24,03 мм.

Определим время при пожаре от начала воспламенения древесины до наступления предельного состояния конструкции по огнестойкости:

t_cr = Z_cr / V = 24,03 / 0,6 = 40,05 мин,

где V - скорость обугливания древесины, (приложение 1, таблица 1).

Фактический предел огнестойкости балки составляют:

Пф = t_зо + t_cr = 5 + 40,05 = 45,05 мин

где t_зо – время задержки обугливания, то есть время при пожаре от начала воздействия температуры на древесины до ее воспламенения, равное 5 мин.
Расчет по условию потери устойчивости плоской форм

Потеря устойчивости плоской формы (деформирования) изгибаемых конструкций, находящихся в условиях пожара, зависит не только от глубины обугливания древесины, но также и от возможного выхода из строя нагельных соединений элементов связи.

Поскольку на заданной части длинны (l_pc) время утраты несущей способности стальных креплений связей t_рс = 15 мин.(0,25 ч.), то за это время значение глубины обугливания поперечного сечения балки с учетом того, что время задержки обугливания (t₃₀ = 5 мин.) можно определить, исходя из соотношения:

Z₁ = (t_pc - t_зо) *V = 10 *V = 10* 0,6 = 6 мм.

Для определения критического значения глубины обугливания, из условий сохранения устойчивости плоской формы (деформирования), необходимо:

1. В пределах граничных значений (Z₁ = 6 мм. и Z_i = 0,25*В_б = 42,5 мм.) произвольно выбрать не менее трех значений глубины обугливания:

Z₂ = 16 мм.; Z₃ = 26 мм.; Z₄ = 36 мм.

2. Определить параметры (h/В_б = 5,24) и (Z_cri/h):

Z_cr1 /h = 6/890 = 0,0067;

Z_cr2 /h = 16/890 = 0,0179;

Z_cr3 /h = 26/890 = 0,0292;

Z_cr4 /h = 36/890 = 0,04;

Z_cr5 /h = 42,5/890 = 0,0478.

3. Определить по графикам значения коэффициентов η_w(i):

η_w(1) = 0,9;

η_w(2) = 0,85;

η_w(3) = 0,66;

η_w(4) = 0,52;

η_w(5) = 0,44.

4. Определить значение коэффициентов (φ_fmi) с учетом изменения размеров поперечного сечения в середине пролета балки в результате обугливания древесины с трех сторон по формуле:

φ_fmi = 140 *((В_б – 2* Z_cri)²/l_pc*(h – K* Z_cri))* K_fф*K_fжмi

где K_fф – коэффициент, зависящий от формы эпюры изгибающих моментов на участке (l_pc). Таким образом коэффициент определяется по формулам:

K_fф = 1,75 – 0,75 α_f при l_pc < 0,5L;

K_fф = 1,35 + 1,45 ⋅ (с/l_pc)² при l_pc = 0,5L;

где α_f = M_lpc / M_n; c = l_pc/2;

K_fжм – коэффициент, значение которого для односкатной балки приравнивается к 1;

К – количество сторон балки по высоте ее сечения, подвергающихся обугливанию (при трехстороннем обогреве К=1, при четырех – К=2).

α_f = M_lpc / M_n = 168,75/225 = 0,75;

M_n = q_n *L² / 8 = 12,5 *12² / 8 = 225 кНм;

K_fф = 1,75 – 0,75*0,75 = 1,19.

φ_fw1 = 140 *((0,17 – 2* 0,0067)²/3*(0,89 – 1* 0,0067))* 1,19*1 = 1,57;

φ_fw2 = 140 *((0,17 – 2* 0,0179)²/3*(0,89 – 1* 0,0179))* 1,19*1 = 1,15;

φ_fw3 = 140 *((0,17 – 2* 0,0292)²/3*(0,89 – 1* 0,0292))* 1,19*1 = 0,84;

φ_fw4 = 140 *((0,17 – 2* 0,04)²/3*(0,89 – 1* 0,04))* 1,19*1 = 0,53;

φ_fw5 = 140 *((0,17 – 2* 0,0478)²/3*(0,89 – 1* 0,0478))* 1,19*1 = 0,36.

5. Вычислить величины напряжений в балке от внешней нагрузки, изменяющихся с уменьшением размеров поперечного сечения балки в результате ее обугливания на различную глубину:

σ_fwi = M_n / (φ_fmi *W * η_w3(i))

σ_fw1 = 225 *10³ / (1,57*22,44*10^-3 * 0,9) = 7,1 МПа;

σ_fw2 = 225 *10³ / (1,15*22,44*10^-3 * 0,85) = 10,26 МПа;

σ_fw3 = 225 *10³ / (0,84*22,44*10^-3 * 0,66) = 18,1 МПа;

σ_fw4 = 225 *10³ / (0,53*22,44*10^-3 * 0,52) = 36,38 МПа;

σ_fw5 = 225 *10³ / (0,36*22,44*10^-3 * 0,44) = 63,3 МПа.

6. Построить график зависимости напряжения от глубины обугливания (рис. 4.1) и при значении напряжения, равном (σ_fw = R_fw), определить критическую глубину обугливания.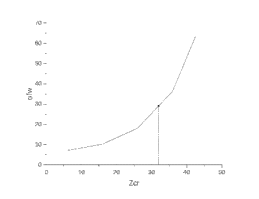



Рис. 4.1 График зависимости напряжения от глубины обугливания

t_cr = Z_cr / V = 32 / 0,6 = 53,3 мин;

П_ф = t_зо + t_cr = 5 +53,3 = 58,3 мин. = 0,972 ч.
Вывод: Фактический предел огнестойкости балки принимают значение Пф, которое наступает по третьему условию потере устойчивости плоской формы Пф = 58,3 мин. = 0,972 ч.