ЭСА лек.. Содержание введение датчики
 Скачать 1.19 Mb.
|
|
Законы алгебры логических схем Работу любой логической схемы можно описать математическими зависимостями. Правила построения таких формул базируются на знаниях Булевой алгебры. Особенностью которой, является использование в расчетах двоичной системы счисления. Для анализа и синтеза логических зависимостей справедливы следующие аксиомы и тождества:  ,  ,  ; ,  ,  ,  ; ,  ; ,  , (коммутативность); ,  , (ассоциативность); ,  , (дистрибутивность); ,  ,  , (идемпотентность); ,  , (поглощение); ,  , (склеивание); ,  , (правило де Моргана); ,  , (правило де Моргана);В качестве примера применения вышеуказанных тождеств, упростим выражение:  Здесь, по порядку действий применяется: сначала правило де Моргана , затем аксиома , далее закон дистрибутивности , после и совместно с , . В итоге получаем заметное упрощение исходной функции.Проверку правильности проведенных преобразований можно сделать, составив так называемые таблицы истинности, для исходной и упрощенной формул. Такая таблица представляет собой зависимость значений выходной величины от всех возможных двоичных комбинаций входных переменных. Так например для рассмотренных выше логических элементов И, ИЛИ, НЕ по их математическим функциям можно составить следующие таблицы истинности:
Аналогичную таблицу можно составить не только для отдельно взятого элемента, но и для целой логической схемы. Чтобы определить число возможных комбинаций входных сигналов, следует основание системы счисления возвести в степень равную числу входных переменных. Так, например, для схемы на рисунке 63 при четырех входных переменных, число комбинаций равно  . Для простоты построения таблицы истинности эти комбинации лучше всего представить в виде числовой последовательности от 0 до  в двоичном формате (где: 2 – основание системы счисления, а  - число входных переменных). Состояния выходного сигнала определяется по математической формуле путем прямой подстановки в нее значений входных переменных.При решении практических задач, как правило, синтез логических схем начинается не с математической формулы, а именно с таблицы истинности, которая составляется исходя из заданных технических условий. Анализ и синтез комбинационных и последовательностных логических схем Комбинационная – это такая логическая схема, у которой в один и тот же момент времени состояние выходных сигналов напрямую зависит от состояния входных. Для анализа и синтеза комбинационных логических схем применяют различные методы, в частности составление совершенной дизъюнктивной или конъюнктивной нормальной формы (СДНФ, СКНФ). Для СДНФ выходные переменные (таблицы истинности) имеющие единичное значение подвергаются логическому суммированию, входящие в них входные переменные – логическому перемножению, причем представленные нулевой величиной берутся с инверсией, а единичной – без инверсии. Для СКНФ - выходные переменные (таблицы истинности) имеющие нулевое значение подвергаются логическому перемножению, входящие в них входные переменные – логическому суммированию, причем представленные единичной величиной берутся с инверсией, а нулевой – без инверсии. Выбор нормальной формы целесообразно делать в зависимости от того нулевых или единичных значений больше в колонке «y» заданной таблицы истинности. Рассмотрим пример, в котором три входных переменных и одна выходная, заданы таблицей истинности. (СДНФ)  (СКНФ) 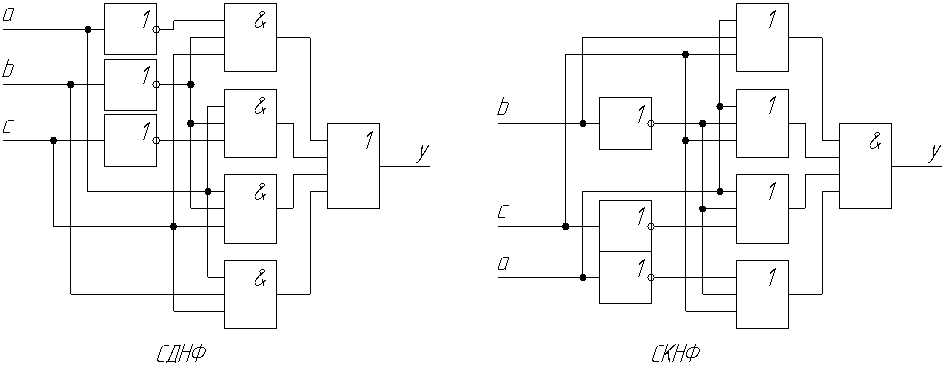  Рис. 64. «Реализация СДНФ и СКНФ на логических элементах» Таблица 6. «Исходная таблица истинности»
Реализуем полученные функции на логических элементах (Рис. 64). Таким образом, можно реализовать практически любую функцию с конечным числом входных и выходных переменных. Единственным недостатком такого способа построения логических схем является их громоздкость (особенно при большом числе входных и выходных переменных). В значительной мере этот недостаток устраним, с применением различных способов минимизации. В частности метод составления минимизированной дизъюнктивно нормализованной формы (МДНФ) при помощи карт Карно. Для примера возьмем СДНФ, составленную для таблицы 6, и все ее составляющие занесем на диаграмму (Рис. 65). Принцип построения такой диаграммы сводится к выделению тех клеток, которые оказываются на пересечении строк и столбцов входных переменных. Затем необходимо объединить соседние по вертикали или горизонтали клетки. Объединять можно  клеток, где:  . При объединении следует помнить, что карты Карно можно «сворачивать» по вертикали и горизонтали (так на рис. 65 объединены верхняя левая и правая клетки). Одиночно стоящие клетки не объединившиеся ни с кем в МДНФ входят неминимизированными.Последним этапом минимизации является написание МДНФ. По карте Карно, для объединенных групп запишем математическую формулу: (МДНФ) 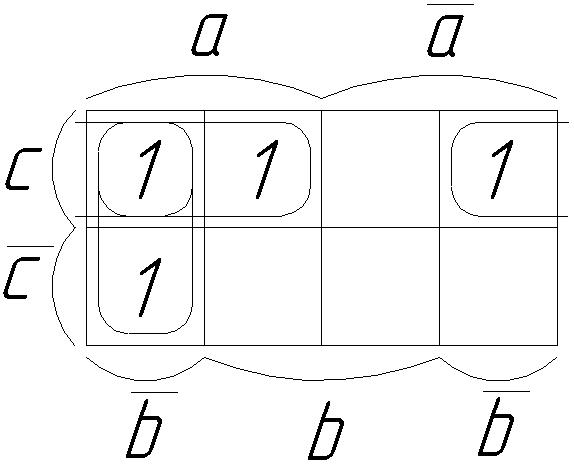 . Рис. 65. «Карта Карно» Составим по МДНФ схему на логических элементах и сравним, насколько упростилась схема по сравнению со схемой СДНФ (Рис. 66). 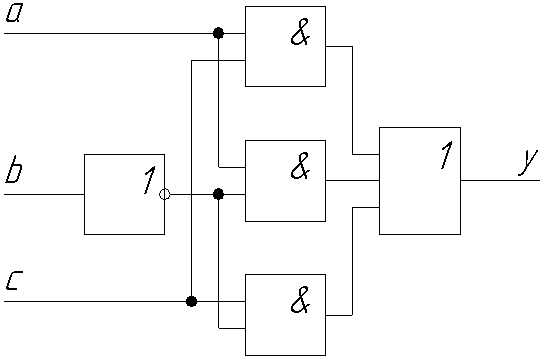 Рис. 66. «Реализация МДНФ на логических элементах» В дальнейшем, при необходимости, и эту схему можно преобразовывать, видоизменять, упрощать, приводить к определенному базису и т.п. при помощи тождеств, приведенных в начале главы. Примерами комбинационных логических схем, применяемых в автоматике являются: шифраторы, дешифраторы, мультиплексоры, демультиплексоры, некоторые виды сумматоров и т.д. Последовательностные логические схемы имеют в своем составе так называемые элементы памяти (всевозможные триггеры). То есть в последовательностных схемах значение выходной величины зависит не только от состояния сигналов на входах, но и от состояния элементов памяти, входящих в данную схему. Способы анализа и синтеза последовательностных схем мало отличаются от анализа и синтеза комбинационных. Основное различие заключается в том, что необходимо при составлении таблиц истинности учитывать влияние элементов памяти и по возможности, уметь разделять такую схему на комбинационную и дополняющую ее схему с элементами памяти. Примеры последовательностных логических схем с реализацией на релейно-контактной базе приведены на рисунке 67. Принцип работы схемы изображенной на рис. 67,а: схема изображена в исходном состоянии, на реле  питание не подается, лампа  не горит. При кратковременном нажатии кнопки  , по цепи ключ  , ключ подается питание на реле , реле срабатывает и замыкает пару контактов  и  . Срабатывание контакта позволяет неограниченно долго питать катушку реле , а срабатывание контакта на тот же период времени питать сигнальную лампу . Перевести схему в исходное состояние можно кратковременным нажатием кнопки . В этом случае цепь питания катушки реле разомкнется, а вместе с ней разомкнуться контакты и , питающие катушку реле и сигнальную лампу .Таким образом приведенная выше схема обладает свойством «запоминания» последнего события и по своему принципу работы аналогична работе  -триггера.Схема изображенная на рис. 67,б обеспечивает не только «запоминание» последнего события, но и взаимное исключение одновременного срабатывания двух реле. Такое схемное решение широко применяется, например, при реверсировании привода. Когда необходимо не только поменять полярность питания двигателя, но и отключить предыдущее состояние работы. К примеру, выключить лампу 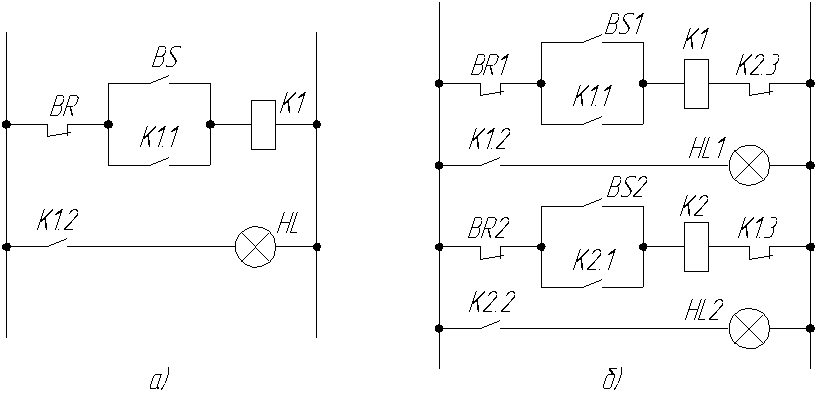 можно нажатием кнопки  , а можно нажатием кнопки  , но уже с одновременным включением лампы  . Это обеспечивается применением реле с дополнительным размыкающим контактом, установленным последовательно цепи питания катушки. Рис. 67. «Последовательностные логические схемы: а) с одним элементом памяти; б) с двумя элементами памяти» Схемы, приведенные на рис. 67 широко применяются в современной аппаратуре автоматизации. В ряде случаев аналогичную схему можно выполнить и на логических элементах, применив вместо силовых реле полупроводниковые тиристоры и IGBT-модули. 5. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
