Спектральный анализ сигналов
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
П.1. НЕКОТОРЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ ФОРМУЛЫ ПРИВЕДЕНИЯ cos(90o ± α) = ± sin α , sin(90o ± α) = + cos α , tg(90o ± α) = ±ctgα , cos(180o ± α) = − cos α , sin(180o ± α) =± sin α , tg(180o ± α) = ±tgα , cos(270o ± α) = ± sin α , sin(270o ± α) = − cos α , tg(270o ± α) = ±ctgα , cos(360o − α) = + cos α , sin(360o − α) = − sin α , tg(360o − α) = −tgα . ФОРМУЛЫ СУММЫ И РАЗНОСТИ УГЛОВ И ФУНКЦИЙ cos(α ± β) = cos α cosβ m sin α sin β , sin(α ± β) = sin α cosβ ± cos α sin β , cos α + cosβ = 2 cos[(α + β) / 2]cos[(α − β) / 2] , cos α − cosβ = −2sin[(α + β) / 2]sin[(α − β) / 2] , sin α + sin β = 2sin[(α + β) / 2]cos[(α − β) / 2] , sin α − sin β = 2 cos[(α + β) / 2]sin[(α − β) / 2] . ФОРМУЛЫ ПРОИЗВЕДЕНИЯ ФУНКЦИЙ cos α cosβ = 0.5[cos(α − β) + cos(α + β) , sin α sin β = 0.5[cos(α − β) − cos(α + β) , sin α cosβ = 0.5[sin(α − β) + sin(α + β) . ФОРМУЛЫ КРАТНЫХ АРГУМЕНТОВ cos2α = 0.5(1 + cos 2α) , cos 3 α = (3 / 4) cos α + (1/ 4) cos 3α , cos4α = 3 / 8 + (1/ 2) cos 2α + (1/ 8) cos 4α , cos5α = (5 / 8) cos α + (5 /16) cos 3α + (1/16) cos 5α , sin2 α = 0.5(1 − cos 2α) , sin 3 α = (3 / 4) sin− (1/ 4) sin 3α , sin4α = 3 / 8 − (1/ 2) cos 2α + (1/ 8) cos 4α , sin5α = (5 / 8) sin α − (5/16) sin 3α + (1/16) sin 5α . ФОРМУЛЫ ДВОЙНЫХ, ТРОЙНЫХ И ПОЛОВИННЫХ УГЛОВ sin 2α = 2sin α cos α , cos 2α = cos2 α − sin2 α = 1 − 2sin2 α = 2cos2 α −1, cos 3α = 4cos3 α − 3cos α , sin 3α = 3sin α − 4sin3 α , cos(α /2)= ±√0.5(1 + cosα) sin(α /2)= ±√0.5(1 − cosα) ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ shx = (ex− e−x) / 2 , sin x =− jsh( jx) = (e jx− e −jx) / 2 j , chx = (ex+ e−x) / 2cos x = ch( jx) = (e jx+ e−jx) / 2 , e jωt= cosωt + j sinωt , e−jωt= cosωt − j sinωt . П.2. ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ  П.3. НЕКОТОРЫЕ ИНТЕГРАЛЫ ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ  ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ X = a2+ x2
П.4. ОСНОВНЫЕ ТЕОРЕМЫ О СПЕКТРАХ Вычисление выражений (2.13) и (2.14) для некоторых импульсных сигналов приведены в книге А. А. Харкевича “Спектры и анализ” (М.: Физматгиз, 1962. – 236 с.). 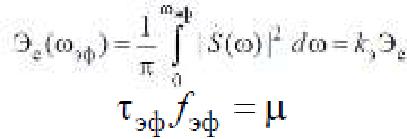 Выбирая kэ = 0.9 , получим результаты, приведенные в табл. П.1. Здесь μ = τэ ⋅ fэ.  Значение μ =τэ⋅ fэ оказывается наибольшим у импульсов, характеризующихся разрывом функции (экспоненциальный и прямоугольный импульсы), меньшим – у импульсов с разрывом первой производной S’(t) (треугольный и косинусоидальный) и самым малым – у колокольного импульса, характеризующегося непрерывностью как функции S(t), так и всех ее производных. Из рассмотренного следует, что эффективная ширина спектра импульса связана с его длительностью зависимостью fэ = μ / τэ, где μ – коэффициент, зависящий от формы импульса и принятого уровня полной энергии, а следовательно, и уровней τ и f. Выбирая kэ= 0.95 (95 %),получаем результаты,приведенные в табл.П.2,взятой из книги Я.С. Ицхоки “Импульсные устройства” (М.: Советское радио, 1959. – 728 с.). Оценку эффективной ширины спектра импульса можно произвести также с помощью графика рис. П.1. На нем и в табл. П.2 приняты обозначения: τ0.5 –длительность импульса, измеряемая на половинном уровне от амплитуды(.5U); tфа – активная длительность фронта, определяемая разностью соответствующих моментов времени достижения импульсом значений 0.9U и 0.1U.   П.6. СВЯЗЬ МЕЖДУ ИЗОБРАЖЕНИЕМ ПО ЛАПЛАСУ И ОРИГИНАЛОМ
|
