Спектральный анализ сигналов
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
1t | | | | cos n1t. | | | | | | | | | | |||||||||||||||||||||||
| | | | | | | | | | | | | | | | | | | | | | | |||||||||||||||
| | | | | | | 2 | | | 2 | 1 | | | | | | | | | | |||||||||||||||||
| | | | | | | | | | | | | | | n2,4,6n | | | | | | | | | | | | | | | | |||||||
| сns bn | 2 | 1 2 T 2 | s t sin n1t dt | 2E | | cos | n1T | | ||||
| | | | | | 1 | | , | | ||||
| 2 T T2 | nT1 | | | |||||||||
| | | | | | 2 | | ||||||
-
0,
n 0, 2, 4,
или сns
E
1 cos n
2E
. Окончательно можно записать
n
, n 1, 3, 5,
n
-
4 E
1
1
s t 2
cos n1t 2
cns
sin 1t
sin 31t
sin 51t
.
3
5
n1,3,5,
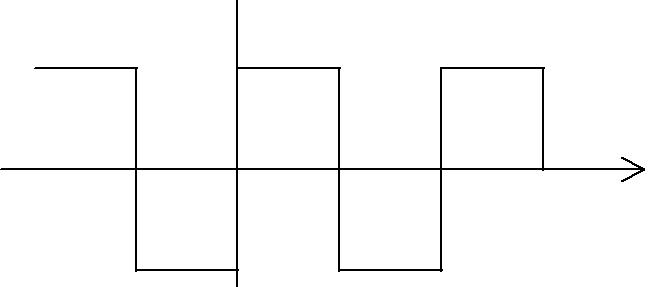
Пример 1.3. Найдем по формуле (1.3) спектр сигнала, представленного на рис. 1.3:
-
E
t
-T/2
0
T/2
T
Рис. 1.3.
Произведя аналогичные предыдущим примерам вычисления, получим: a0/2=E/2;
-
a
2E
T 2 cos n tdt 0;
n
T
1
0
T 2
0,
n 2, 4, 6,
bn
2E
sin n1tdt
E
1 cos n 2E
.
n
T
0
, n 1, 3, 5,
n
-
В итоге, сигнал представляется как s t
E
2 E
1
1
sin 1t
sin 31t
sin 51t
.
2
3
5
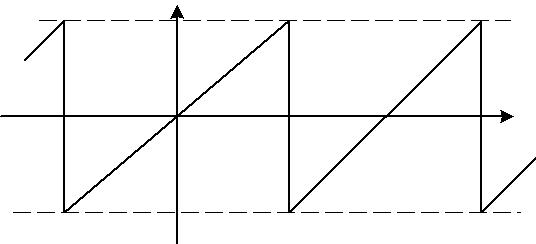
Пример 1.4. Разложение пилообразного колебания рис. 1.4 имеет вид
s(t)
E
T
t
0
Рис. 1.4
-
s t
2 E
1
1
1
sin 1t
sin 21t
sin 31t
sin 41t
.
2
3
4
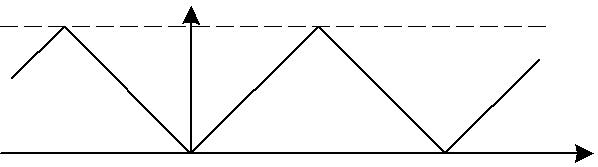
Пример 1.5. Разложение последовательности униполярных треугольных импульсов имеет вид
s(t)
E
t
0 T
Рис. 1.5
| s t | E | | | 4 | | | | | | | 1 | | | | | | | 1 | | | | | ||||||||||||
| | | | | | | | | (cos 1t | | | | | cos 31t | | | | sin 51t | . | | |||||||||||||||
| | 2 | | | | 2 | | | 5 | 2 | | | | ||||||||||||||||||||||
| | | | | | | | | | | 3 | | | | | | | | | | | | | ||||||||||||
| Пример 1.6. Разложение последовательности униполярных прямоугольных | | |||||||||||||||||||||||||||||||||
| импульсов имеет вид | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | s(t) | | | | | | | | | | | | | |||||
| | | | | | | | | | | | | | | | | | E | | | | | | | | | | | | | | | | ||
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | t | | | |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |||||
| | | | | | | | | | | | -τ/2 0 τ/2 | | | T | | | | | | | | | ||||||||||||
| | | | | | | | | | | | | | | | Рис. 1.6 | | | | | | | | | | | | ||||||||
| | | | | | | | | | | | 2 | | | | 1 | | n | | | | | | | | | |||||||||
| | s t | E | | | | | | | | | | | sin | 1 | | cos n1t . | | | ||||||||||||||||
| | | | | | n | | 2 | | | | | |||||||||||||||||||||||
| | | | | | | | | | T | | | | n1 | | | | | | | | | | | | | | ||||||||
1.2.Непериодические сигналы
Непериодические сигналы отличаются от периодических тем, что не имеют периода повторения. Формально – это периодические сигналы с периодом T . Формулы для рядов Фурье при этом трансформируются в преобразования Фурье
S () s t e jt dt ,
и обратные преобразования Фурье
-
s t
1
S () e jt d.
2
Полезно ознакомиться со свойствами преобразования Фурье [1], наиболее важные из которых: линейность; сдвиг сигнала по времени; изменение масштаба времени; дифференцирование сигнала; интегрирование сигнала; произведение сигналов; взаимозаменяемость частоты и времени в преобразованиях Фурье.
Между формулами для рядов и преобразований Фурье существует простая связь
сnT1 S ( n 2T),гдеS()-спектр непериодического сигналаs(t),асn-спектрпериодического сигнала s пер (t) , полученного из s(t) путем повторения с периодом T,
sпер(t ) s (t nT ).
n
Пример 2.1. Симметричный прямоугольный импульс можно определить как
| | E при t (,), | . Спектральная плотность после вычисления интеграла Фурье | | ||||||
| s(t) | | | |||||||
| 0 при t остальных | | | | | | | | | |
| имеет вид | | | | | | | | | |
| | | | sin | | | | | ||
| | | | | | |||||
| | | S () s t e jt dt E | | 2 | . | | |||
| | | | | | |||||
| | | | | | | | | | |
| | | | | | | | | | |
2
Пример 2.2. Симметричный треугольный импульс аналогично прямоугольному импульсу представляется спектром
-
2
Esin
S ()
4
.
2
4
-
Пример 2.3. Колоколообразный или
гауссов
импульс,
определяемый как
s(t) Eet 2 / 2 a2 имеет спектр S ( )
aEea22/ 2.
2
Пример
2.4.
Импульс
вида
sinc(x),
определяемый
выражением
s t sin c (mt)
sin
m
t
2m / при ( m
, m ),
, имеет спектр S()
.
mt
0 при остальных
Пример 2.5. Сигнал вида e(t)=s(t)cos(0t+0) при относительно больших 0 относительно частотных составляющих спектра s(t) относится к узкополосным сигналам и обладает важными для практики свойствами. Используя к e(t) преобразование Фурье,
-
e
j
e
j
s t cos0 t 0
e jt dt
0
s t e j 0
t dt
0
s t e j 0
t dt .
2
2
Первый интеграл в правой части есть спектральная плотность функции s(t) при частоте -0, а второй интеграл – при частоте +0. Поэтому полученное выше выражение можно записать в виде
-
st cos0t 0ejt dt
1
e0 S 0 e0 S 0,
2
где S – спектральная плотность колебания s(t).
Если s(t) – периодическое колебание, имеющее линейчатый спектр, то спектр узкополосного сигнала будет также линейчатым, расщепленным на две части и сдвинутым соответственно на -0 и 0 по оси частот. Таким образом, при модуляции сигналом
st E1signsint
высокочастотного сигнала cos0t спектр колебания
et st cos0t
будет представлять расщепленный спектр сигнала s(t), соответственно сдвинутый по оси частот на величину -0 и 0.
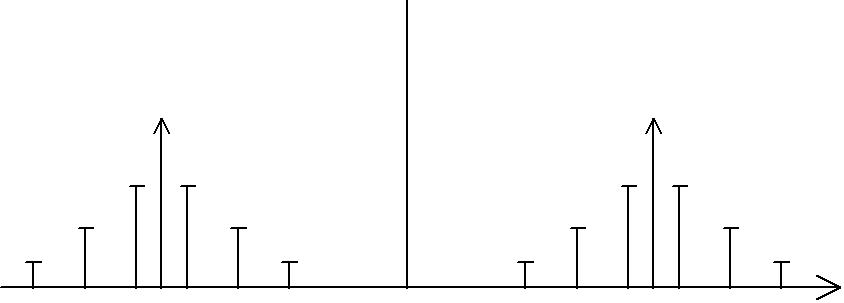
При модуляции исследуемого сигнала высокочастотным гармоническим колебанием cos0t спектр результирующего колебания будет представлять расщепленный на два и сдвинутый соответственно на 0 и -0 спектр модулирующего сигнала (рис. 1.7, а). Таким образом результирующий спектр будет иметь вид (рис. 1.7, b).
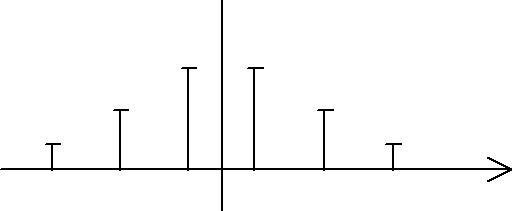
-51 -31 -1 0 1 31 51
Рис. 1.7 а
-
S(+0)/2
S(-0)/2
-
-0
0
0
Рис. 1.7 б
Если известна функция s(t), то определение параметров ряда Фурье с помощью выражений (1.3), (1.4) называется задачей спектрального анализа. Амплитудный спектр сигнала, т.е. зависимость амплитуд гармоник от частоты, может быть определен с помощью специального прибора – анализатора спектра. Если известны параметры ряда Фурье, то определяя сумму в правой части (1.3) для определенного числа членов, можно восстановить функцию s(t). Это будет задача синтеза сигнала (синтез по Фурье). Теоретически может определяться сумма бесконечного числа членов ряда (1.3). Тогда ряд Фурье восстанавливает функцию s(t) точно (кроме, может быть, отдельных точек). При суммировании же конечного числа членов ряда аппроксимация функции s(t) получается приближенной. Расхождение между функцией s(t) и суммой конечного числа членов ряда
тем больше, чем меньше N.
Домашнее задание
Рассчитать и построить нормированные амплитудные спектры сигналов, исследуемых в лабораторной работе: 1) гармонический сигнал; 2) сигнал в виде последовательности треугольных импульсов; 3) пилообразный сигнал. По оси ординат откладывать нормированную амплитуду гармоник (An/A1), по оси абсцисс – нормированную частоту n.
Лабораторное задание
C помощью компьютерного анализатора спектра, построенного с использованием пакета LabView, получить и построить амплитудные спектры сигналов.
Используя данные о параметрах спектральных составляющих, указанных преподавателем сигналов, произвести с помощью компьютера синтез Фурье. Исследовать влияние числа суммируемых гармоник N на правильность восстановления формы сигнала.
Описание лабораторного макета
Лабораторный макет представляет собой компьютерную модель анализатора спектра, построенного в среде LabView и представлен на рис. 1.8.
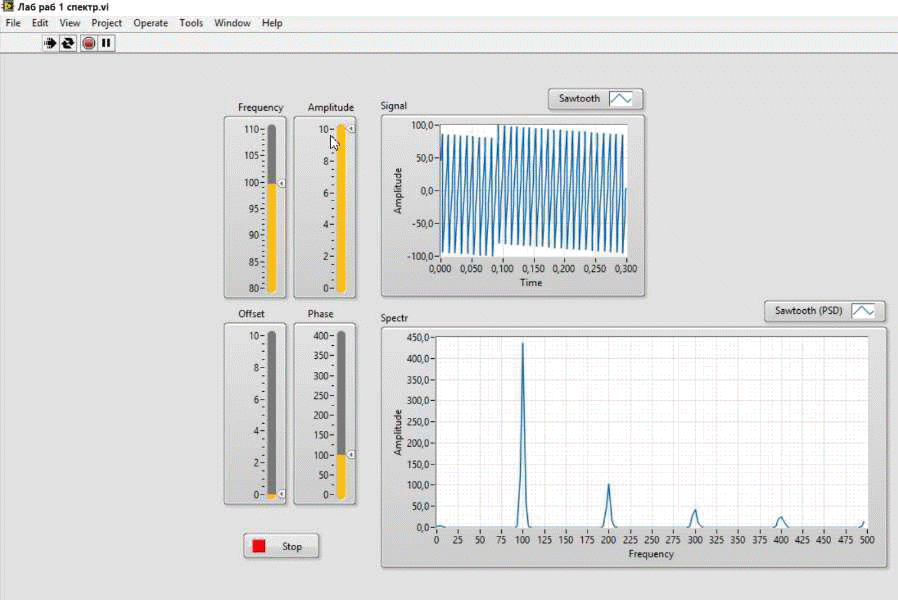
Рис. 1.8
Блок-схема модели имеет вид (см. рис. 1.9) и содержит блоки: Simulate Signal – источник моделируемого сигнала; Frequency, Offset, Phase, Amplitude – регулировки частоты, постянного уровня, фазы и амплитуды соответственно; Spectral Measurements – спектральный анализатор; Signal, Spectr – индикация спектра и сигнала.
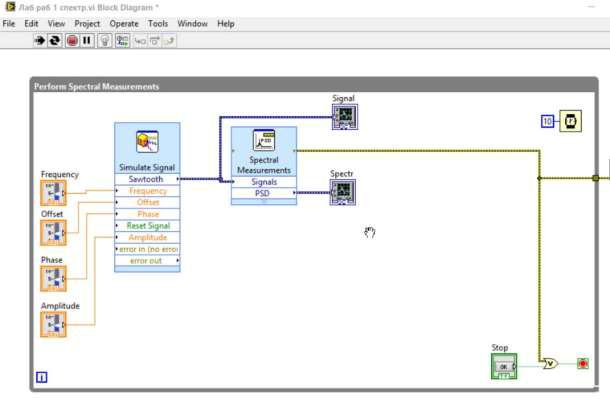
Рис. 1.9
Рекомендуемые параметры блоков представлены на скриншотах рис. 1.10 и рис.
1.11.
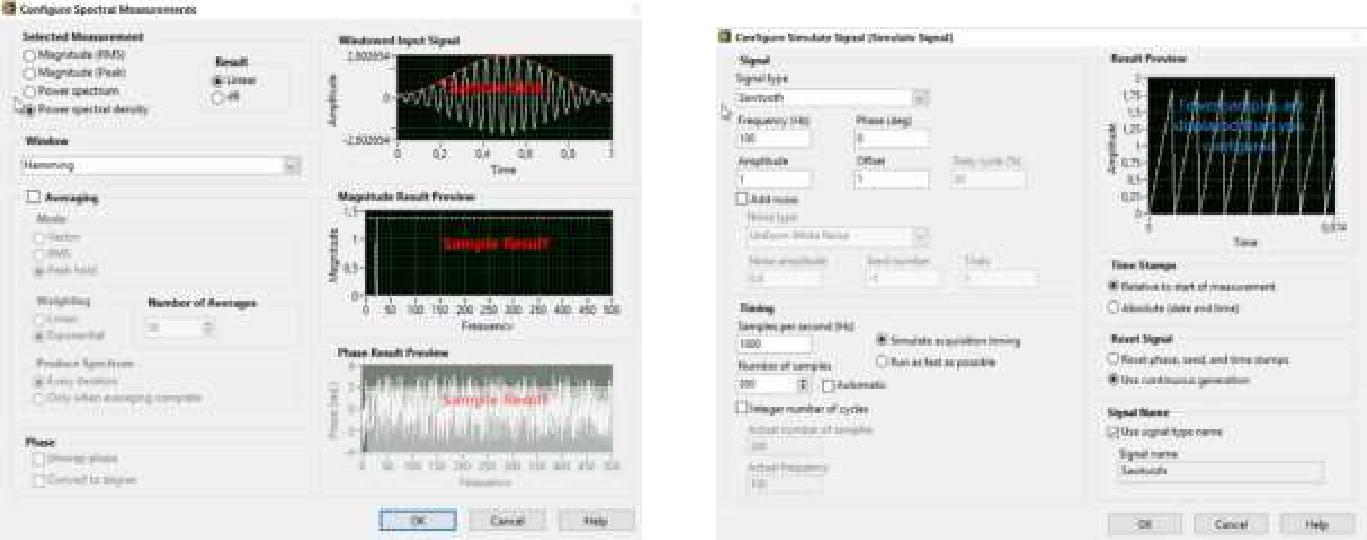
Рис. 1.10 Рис. 1.11
Порядок выполнения работы.
5.1. Останавливая работу программы переходим к блок-схеме.
5.2. В источнике сигнала выбираем требуемый вид сигнала.
5.3. Запускаем программу.
5.4. Производим настройку сигнала с помощью органов регулирования параметрами сигнала.
5.5. Зарисовываем полученные данные (делаем скриншот).
5.6. Переходим к рассмотрению следующего вида сигнала. Для этого возвращаемся
5.1.
5.6. Производим обработку полученных данных: сравниваем полученные спектры с теоретическими спектрами, полученными из формул и расчетов; проверяем справедливость для практических спектров свойств спектра, например, значения спектра на нулевой частоте, соотношения длительности сигнала и ширины спектра и т.д.
Содержание отчета
Графики расчетных и измеренных анализатором спектра амплитудных спектров
сигналов.
Распечатки временных функций, полученных на компьютере.
Основные выводы по лабораторной работе, включающие анализ расхождения теоретических и экспериментальных данных.
Контрольные вопросы
Основные различия и характерные особенности спектров синусоидального, однополярного синусоидального колебания и колебания типа «меандр» одинаковой частоты.
Чем определяется ширина спектра колебания с амплитудной модуляцией?
Сходство и различие модулирующего, модулированного и модулируемого колебаний.
Можно ли считать исследуемые колебания узкополосными? Ответ обосновать, исходя из определения узкополосных радиосигналов.
Как влияет период повторения периодического сигнала на его спектр?
Как влияет число гармоник, участвующих в синтезе по Фурье, на форму получаемого сигнала?
Как влияет форма синтезируемого сигнала на число гармоник, которые необходимо использовать при его синтезе?
Рекомендуемая литература
Гоноровский И. С. Радиотехнические цепи и сигналы: учеб. Пособие для вузов / И.С. Гонорвский. 5-е изд., испр. и доп. М.:Дрофа, 2006. 719 с.: ил.
Баскаков С. И. Радиотехнические цепи и сигналы: Учеб. Для вузов по спец. «Радиотехника». 3-е изд., перераб. и доп. М.: Высш. шк., 2000. 462 с.: ил.