Инж. инж мех (копия). Статика Бос жне бос емес дене. Байланыстар жне оларды реакциялары. Жиі кездесетін байлансытар трлері. Босату принципі
 Скачать 1.78 Mb.
|
|
14. Сырғанау үйкелісінің зандары. Статикалық және динамикалық үйкеліс коэффициенті. Үйкеліс бұрышы. Үйкеліс конусы Тәжірибе көрсеткендей, бір денені екінші дененің бетіне дененің жанасу жазықтығында жылжыту кезінде олардың салыстырмалы сырғуына қарсылық күші пайда болады, бұл жылжымалы үйкеліс күші деп аталады.Үйкелістің пайда болуы, ең алдымен, беттердің кедір-бұдырлығына байланысты, бұл қозғалысқа қарсылықты тудырады және бір-біріне басылған денелерде адгезияның болуы.үйкеліс құбылысының барлық ерекшеліктерін зерттеу өте күрделі физика-механикалық проблема болып табылады, оны қарастыру Теориялық механика курсынан асып түседі. Бұл пропорционалдылық коэффициенті динамикалық үйкеліс коэффициенті немесе қозғалыс кезіндегі үйкеліс коэффициенті деп аталады) н статикалық үйкелісті білдіру үшін енгізілген / әрпімен де белгіленеді. Мұндай белгілеу негізсіз енгізілген жоқ, өйткені, кем дегенде, өте өрескел жуықтауда, статикалық және динамикалық үйкеліс коэффициенттері де сәйкес келеді. [c.53] Барлық жоғарыда жазылғанға қараса, к трению сырғу кезінде тыныштықта. Қозғалыс кезінде үйкеліс күші қозғалысқа қарама-қарсы жаққа бағытталған және қалыпты қысымға динамикалық үйкеліс коэффициентінің көбейтіндісіне тең Инженерлік есептеулерде, әдетте, үйкеліс құбылысының негізгі ерекшеліктерін практика үшін жеткілікті дәлдікпен көрсететін ориентальды жолмен белгіленген бірқатар заңдылықтардан туындайды. Демалу кезінде сырғанау үйкеліс заңдары деп аталатын бұл заңдылықтарды келесідей тұжырымдауға болады. 1. Бір денені дененің жанасу жазықтығында екінші дененің бетіне жылжыту кезінде үйкеліс күші (немесе адгезия күші) пайда болады, ол кез-келген мәнді нөлден үйкеліс күші деп аталатын мәнге дейін қабылдай алады.Денеге қолданылатын үйкеліс күші Денеге әсер ететін күштер оны жылжытуға бейім жаққа қарама-қарсы бағытта бағытталған. 2. Шекті үйкеліс күші қалыпты қысымға немесе қалыпты реакцияға статикалық үйкеліс коэффициентінің көбейтіндісіне сандық тең:Үйкелістің статикалық коэффициенті-өлшемсіз шама; ол эмпирикалық жолмен анықталады және жанасатын денелер материалына және беттердің күйіне (өңдеу сипаты, температура, ылғалдылық және т.б.) байланысты болады. 3. Үйкеліс күшінің шекті мәні үйкеліс кезінде жанасатын беттердің мөлшеріне байланысты емес. Бұл пропорционалдылық коэффициенті динамикалық үйкеліс коэффициенті немесе қозғалыс кезіндегі үйкеліс коэффициенті деп аталады) н статикалық үйкелісті білдіру үшін енгізілген / әрпімен де белгіленеді. Мұндай белгілеу негізсіз енгізілген жоқ, өйткені, кем дегенде, өте өрескел жуықтауда, статикалық және динамикалық үйкеліс коэффициенттері де сәйкес келеді. Барлық жоғарыда жазылғанға қараса, к трению сырғу кезінде тыныштықта. Қозғалыс кезінде үйкеліс күші қозғалысқа қарама-қарсы жаққа бағытталған және қалыпты қысымға динамикалық үйкеліс коэффициентінің көбейтіндісіне тең 15. Домалау үйкелісі. Домалау үйкелісінің коэффициенті. Өлшем бірлігі. Домалау шарты. көлбеу жазықтықтағы дененің тепе-теңдік жағдайларын қарастырыңыз, оның бұрышын өзгертуге болады, содан кейін оны алу оңай (оны өзіңіз жасаңыз), дененің φ бұрышы бар жазықтықтан түсе бастайды tgφ=μ , мұндағы μ-дененің жазықтықтағы үйкеліс коэффициенті. Бұл бұрыштың дене салмағына тәуелді емес екендігі таңқаларлық емес пе?Φ бұрышы үшін бірдей өрнекті басқа, мүмкін, қарапайым жолмен алуға болады. Бірақ бұл үшін алдымен "үйкеліс конусы"ұғымымен танысу керек.Материалдық нүкте деп санауға болатын дене өрескел көлденең жазықтықта болсын. Mg тяжести ауырлық күші денені бетіне басады, ал беті денеге n⃗ қалыпты қысым күшімен әрекет етеді . Егер денеге белгілі бір көлденең күш қолданылса, онда беткі жағынан тағы бір күш пайда болады — үйкеліс күші. Көлденең күштің шамасы fтр демалу үйкеліс күшінің максималды мәнінен аспайынша.P. max = μN, дене демалады. Осы мәнге жеткенде, дене қозғала бастайды, ал беті жылжымалы үйкеліс күшімен қозғалысқа кедергі келтіреді Ftr.sk.=Ftr.p.max=μN . Домалау үйкеліс-денелерді бір-біріне домалату кезінде пайда болатын қозғалысқа қарсылық, яғни бір дененің (роликтің) екінші бетінің бойымен тербелуіне қарсылық. Жылжымалы үйкелістің себебі-роликтің және тірек бетінің деформациясы, сондай-ақ адгезия күші. Дақтағы байланыс кернеуі денелердің серпімді және/немесе пластикалық деформациясына әкеледі, бұл беттердің микроскальзациясына, байланыс нүктесіндегі пластикалық ағымға және тұтқыр серпімді гистерезиске әкеледі. Жабысқақ өзара әрекеттесу сияқты, бұл процестердің барлығы термодинамикалық тұрғыдан қайтымсыз және энергияның жоғалуына әкеледі, яғни.жылжымалы қарсылықты тудырады[1]. Бұл жағдайда, әдетте, жылжымалы дене (доңғалақ) тарту немесе тежеу функциясын жүзеге асырмайды деп болжанады (мысалы, вагонның құрамын немесе тежегіш дөңгелегін тездететін Локомотив дөңгелегі), өйткені бұл жағдайда байланыс нүктесінде үйкеліске қосымша шығындар пайда болады, бұл қалыпты байланыс кернеуінен ғана емес, сонымен қатар тангенс, яғни.жылжымалы үйкеліс деп таза жылжымалы үйкеліс түсініледі. F-ұзындықтың өлшемі бар Домалау үйкеліс коэффициенті (өлшемсіз жылжымалы үйкеліс коэффициентінен маңызды айырмашылықты атап өткен жөн); R-жылжымалы дененің радиусы; N-басу күші. Өлшем бирлигы Үйкеліс өзара әрекеттесу аймағында жүретін физика-химиялық процестердің күрделілігіне байланысты үйкеліс процестерін классикалық механика әдістерін қолдана отырып сипаттауға болмайды. Сондықтан үйкеліс коэффициентінің нақты формуласы жоқ. Оның бағалауы эмпирикалық дәлелдер негізінде жасалады: Ньютонның бірінші заңы бойынша дене біркелкі және түзу қозғалады, өйткені сыртқы күш қозғалыс кезінде пайда болатын үйкеліс күшін теңестірсе, Денеге әсер ететін үйкеліс күшін өлшеу үшін денеге қолданылатын күшті өлшеу жеткілікті, сондықтан ол үдеусіз қозғалады б-домалау үйкеліс коэфиценті.Өлшем бірлігі - см Кинематика 1. Нүкте қозғалысының берілу тәсілдері Нүктенің қозғалысы үш тәсілдердің біреуімен берілуі мүмкін. 1. Векторлық тәсіл. М нүктесі Oxyz санақ жүйесіне қатысты қозғалатын болсын. Нүктенің кез келген уақыт мезетіндегі орнын, оның радиус-векторының (4.1 сурет) t уақытына тәуелдігін беріп, анықтауға болады. . (4.1) Бұл векторлық түрде жазылған нүктенің қозғалыс заңы. 2. Координаттық тәсіл. Нүктенің орнын оның уақыт өтуімен өзгеретін координаттарымен тікелей анықтауға болады . (4.2) Бұл - тік бұрышты декарт координаттарындағы нүктенің қозғалыс заңы. 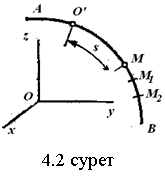 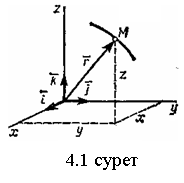 3. Табиғи тәсіл. Нүкте қозғалысын табиғи тәсілмен беру – бұл оның траекториясын (4.2 сурет), траекториясындағы санақ басы мен санақ бағытын және қозғалыс заңын келесі түрде беру . (4.3) 1 Қозғалыс векторлық тәсілімен берілген жағдайда нүктенің жылдамдығы мен үдеуі Нүкте қозғалысының негізгі кинематикалық сипаттамаларының біреуі жылдамдық болып келеді. t уақыт мезетінде радиус-векторымен анықталатын М орнында, ал t1 уақыт мезетінде радиус-векторымен анықталатын М1 орнында болсын дейік (4.3 сурет). Сонда уақыт аралығында нүктенің орын ауыстыруы орын ауыстыру векторымен анықталады. ОММ1 үшбұрышынан болатыны көрінеді, яғни . Орын ауыстыру векторының сәйкес уақыт аралығына қатынасы, нүктенің t уақыт аралығындағы модулі мен бағыты бойынша ортақ жылдамдығы деп аталатын векторлық шамасын береді, . 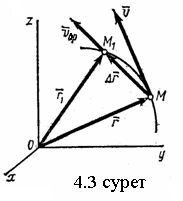 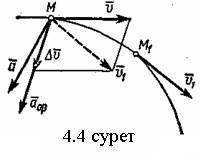  векторлық шамасы нүктенің t уақыт мезетіндегі жылдамдығы деп аталады, сонда нүктенің жылдамдығы векторының t аргументі бойынша бірінші ретті туындысы болып келеді. (4.4) Нүктенің үдеуі - оның жылдамдығының модулі мен бағытының уақыт өтуімен өзгеруін сипаттайтын векторлық шама. Әлдебір t уақыт мезетінде нүктенің орны М және жылдамдығы болсын, ал t1 мезетінде нүкте M1 орнына келіп, жылдамдығына ие болады дейік (4.4 сурет). Сонда уақыт аралығында нүктенің жылдамдығы өсімін алады, ол әрқашан траекториясының ойыс жағына бағытталады. векторының t аралығына қатынасы нүктенің сол ауқыт аралығындағы орташа үдеуін анықтайды. t нөлге ұмтылған кезде ұмтылатын векторлық шама 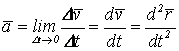 (4.5)нүктенің берілген t уақыт мезетіндегі үдеуі деп аталады. Сонымен, нүктенің берілген уақыт мезетіндегі үдеу векторы жылдамдық векторының уақыт бойынша бірінші ретті туындысына, яғни нүктенің радиус-векторының екінші ретті туындысына тең. 2 Қозғалыс координаттық тәсілімен берілген жағдайда нүктенің жылдамдығы мен үдеуі Келесі теореманы қолданамыз: вектордың туындысының қарастырылатын СЖ-нің қозғалмайтын өсіне проекциясы вектордың сол өске проекциясының туындысына тең. Сонда жылдамдықтың проекциялы үшін келесі орын алады  (4.6)немесе . (4.7) Сонымен, жылдамдықтың координаттық өстерге проекциялары сәйкес координаттардың уақыт бойынша бірінші ретті туындыларына тең. Үдеудің проекциялары үшін келесі болады , , (4.8) немесе , (4.9) яғни үдеудің координаттық өстерге проекциялары жылдамдықтың сәйкес проекцияларының уақыт бойынша бірінші ретті туындыларына немесе кординаттардың екі ретті туындыларына тең. 3 Қозғалыс табиғи тәсілімен берілген жағдайда нүктенің жылдамдығы мен үдеуі Мұнда мен векторларын олардың Мnb табиғи үшжақтықтың М нүктесінен басталып, сонымен бірге қозғалатын өстеріне проекциялары арқылы табылады. Өстердің бағыттары: М - s санағының оң бағытына сәйкес траекторияға жанама бойынша; Мn бас нормалі – траекториямен жанасу жазықтығында траекторияның ойыс жағына жүргізілген нормалі бойынша; Mb бинормалі – алдынғы екі өске перпендикуляр бойынша олармен оң өстер жүйесін құрайтын болып бағытталады. Нүктенің жылдамдығын анықтаймыз 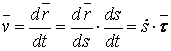 . (4.10)Нүкте жылдамдығының траекториясына жанама өсіне проекциясы . (4.11) Осыдан шығар және жылдамдықтың модулі . Нүктенің үдеуі үшін 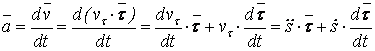 . (4.12)Мұнда 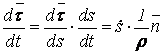 (ρ – қарастырылатын орнында нүктенің траекториясының қисықтық радиусы), сонда, (4.13) яғни үдеу векторы жанама және нормаль құраушыларының қосындысына тең . (4.14) векторы жанасу жазықтығында жатады, яғни Mn жазықтығында. (4.13) теңдігінің екі жағын М, Мn және Mb өстеріне проекциялап, келесіге келеміз 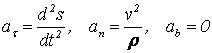 . 4. Абсолют қатты дененің ілгерімелі қозғалысы. Ілгерімелі қозғалыстағы дене нүктелерінің траекториялары, жылдамдықтары және үдеулері туралы теорема. Абсолют қатты дене деп кез-келген екі нүктесінің ара қашықтығы үнемі тұрақты сақталатын, яғни геометриялық формасын өзгертпей сақтайтын денені айтады АҚД-ның қарапайым қозғалыстары: ілгерілемелі қозғалыс; бекітілген өске қатысты айналмалы қозғалыс. Қатты дененің ілгерілемелі қозғалысы деп оның әрбір екі нүктесін қосатын түзулердің кез-келгені өзіне-өзі тек параллель қозғалатындай қозғалыс түрін айтамыз . Ілгерілемелі қозғалыстағы дене нүктелерінің траекториялары кез-келген эквидистанттық (немесе конгурентті) қисық сызықтар болады. Қатты дененің ілгерілемелі қозғалысын кез-келген уақыт мезгілінде дененің барлық нүктелерінің жылдамдықтары тең болатын қозғалыс (перманенттік ілгерілемелі) деп те анықтайды. Демек, қатты дененің Ілгерілемелі қозғалысын сипаттау үшін оның бір ғана нүктесінің қозғалысын зерттесе жеткілікті. Теорема. Егер кез келген дене ілгерілемелі қозғалыста болса, онда оның барлық нүктелері бірдей жылдамдықпен, бірдей үдеумен және бірдей траекториямен қозғалады. 5. Абсолют қатты дененің тұрақты өстен айналмалы қозғалысы. Айналу заңы. Дененің бұрыштық жылдамдығы мен бұрыштық үдеуі. АҚД-ның бекітілген өске қатысты айналмалы қозғалысы деп екі нүктесі қозғалмайтын денені айтады. 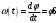 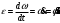 - бұрыштық жылдамдық. - бұрыштық үдеу.  (айналу заңы) 6. Айналмалы қозғалыстағы дене нүктелерінің жылдамдықтары мен үдеуі. Қатты дененің қозғалмайтын ось айналасында айналуымен дененің әр нүктесі шеңбер бойымен қозғалады. Шеңберінің радиусы нүктеден айналу осіне дейінгі қашықтыққа тең. 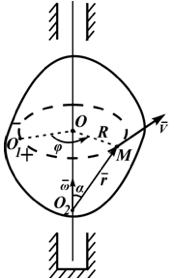 Нүктенің жылдамдығы осындай өрнекпен анықталады: V=dS/dt=dφ∙R/dt=ωR (1) мұндағы ω-қатты дененің айналу жылдамдығы. Тангенциа́льды және қалыпты үдеулердің қосындысы ретінде қозғалыс орнатудың табиғи әдісімен нүктенің үдеуі анықталады: 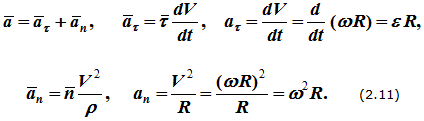 . 7. Айналмалы қозғалыстағы нүкте жылдамдықтары мен үдеулерінің векторлық көбейтінділері түріндегі өрнектер. Эйлер өрнегі. Қозғалыстың кинематикалық сипаттамалары векторлық шамалар 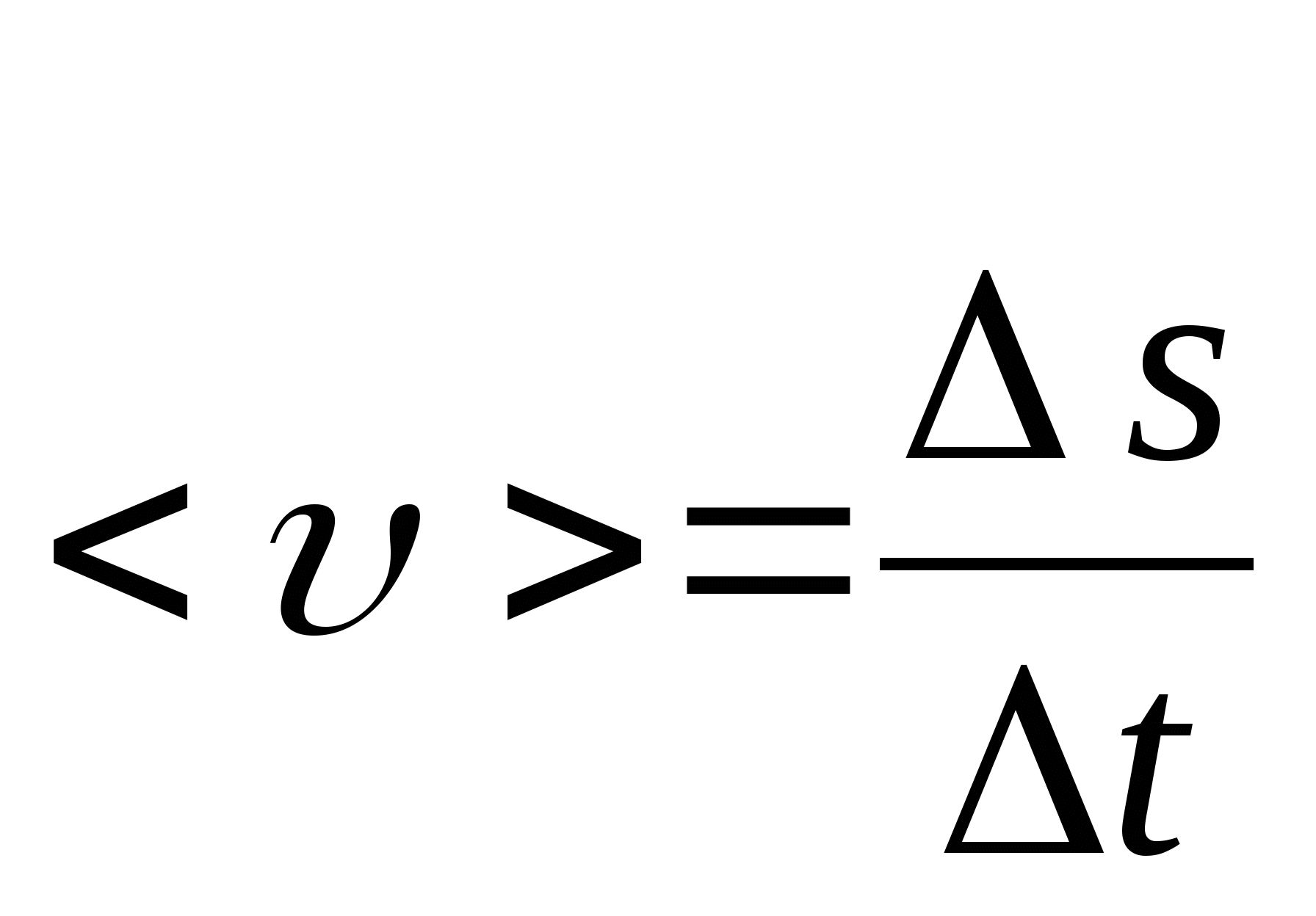 – жылдамдық және  - үдеу болып табылады. Жылдамдық қозғалыстың өзгеру тездігін, сондай-ақ оның берілген уақыт мезетінде бағытын анықтайды.  орташажылдамдық жол өзгерісінің  уақыт өзгерісі  -ға қатынасымен анықталады: .Лездікжылдамдық ұғымын енгізейік. Егер 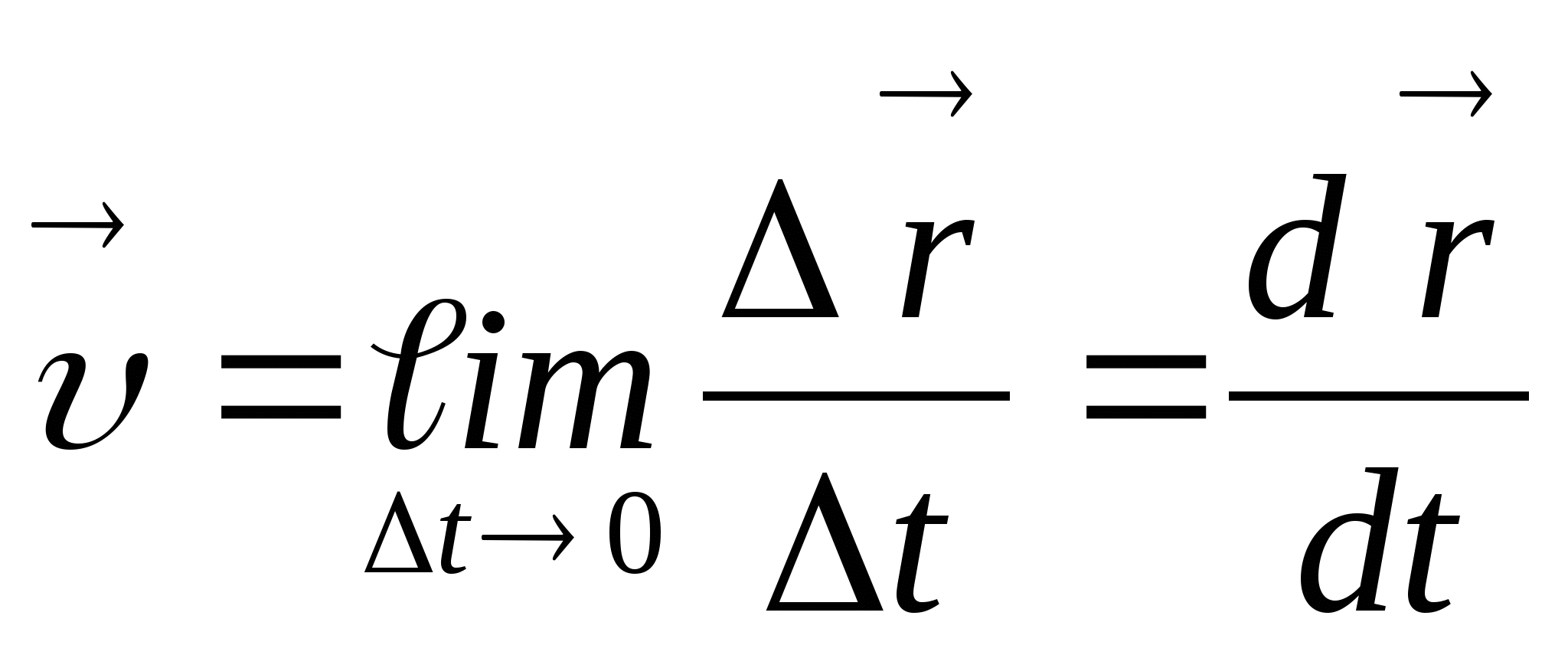 аз уақыт ішінде нүкте  орын ауыстырса, онда уақыт аралығы шексіз азайған кездегі  қатынасының шегі лездік жылдамдық деп аталады, яғни  .Жылдамдық шамасы жол теңдеуінің бірінші туындысы арқылы да анықталады.  өрнегінен  шығады.Бұл материалық нүктенің өте аз dt уақыт ішінде жүрген шексіз аз жолы. Берілген t yақыт ішінде жүрілген жол (1.5.) өрнегін интегралдау арқылы анықталады 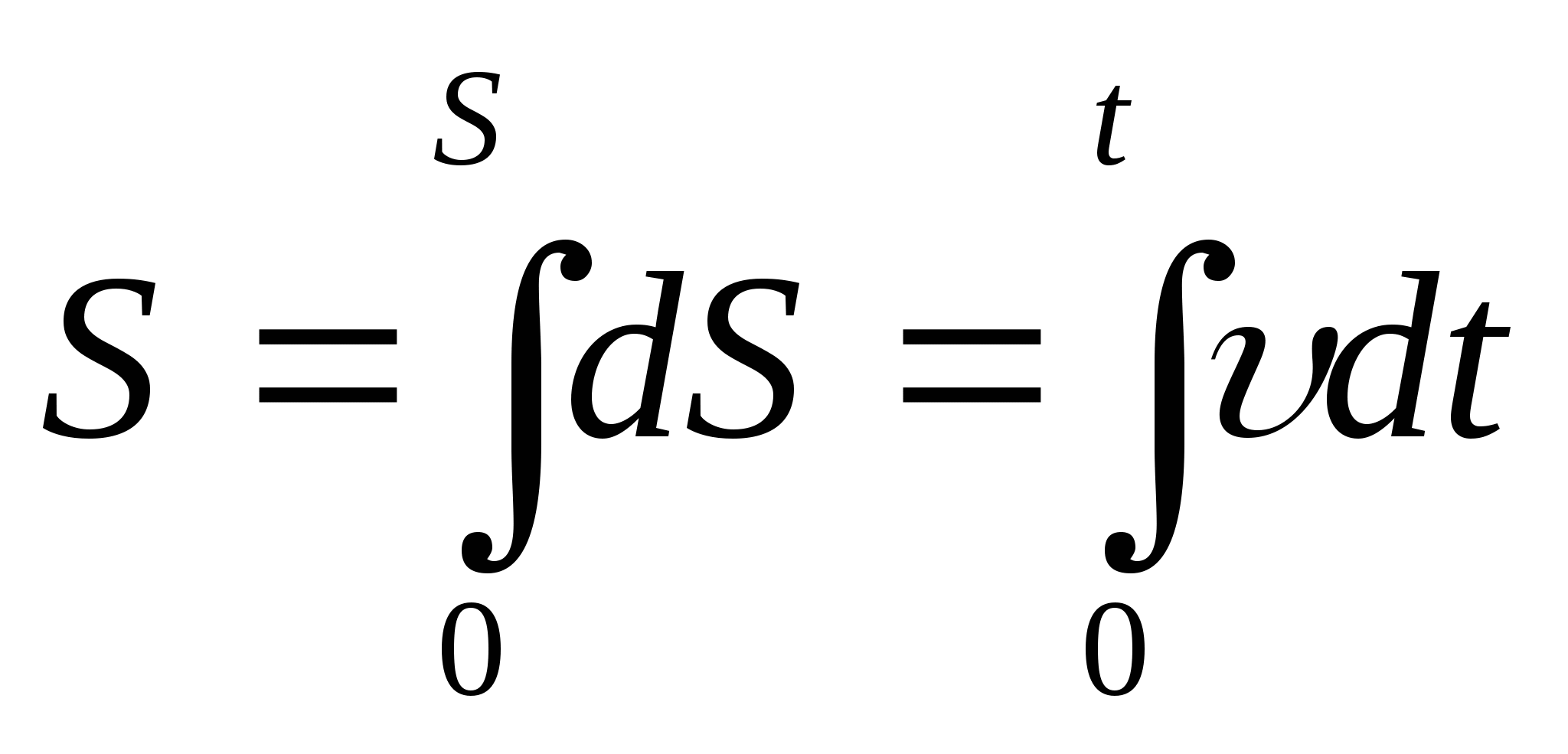 |