Методичка по статистики. Статистическая сводка и группировка. Статистические таблицы
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
Абсолютные статистические величины, характеризуя численность изучаемой совокупности или объемы присущих им признаков, всегда являются числами именованными. В зависимости от сущности изучаемого явления и задач исследования они выражаются в различных единицах измерения: натуральных, трудовых и стоимостных. В учете продукции в натуральном выражении часто применяются условные единицы измерения. Абсолютные статистические величины имеют большое научное и практическое значение. Они широко используются в оценке состояния и развития явлений общественной жизни. На основе абсолютных величин рассчитываются относительные величины. На конкретных примерах, взятых из сообщений Госкомстата Российской Федерации, статистических ежегодников, периодической печати, студенты должны изучить и усвоить многообразие применения относительных величин в решении самых различных задач. При изучении относительных величин также следует уяснить, что они являются не произвольными построениями, а показателями, характеризующими определенные черты общественных явлений. В зависимости от содержания и познавательного значения часто выделяют относительные величины: динамики, планового задания, плана, структуры, координации сравнений, интенсивности и уровня экономического развития. Необходимо хорошо разобраться в различных видах относительных величин, выяснить роль каждого из них в социально-экономическом анализе, а также научиться их вычислять. Относительные величины динамики характеризуют изучаемое явление во времени. Они позволяют при анализе данных, характеризующих развитие явления во времени, выявлять направление развития и измерять темпы роста Относительная величина динамики представляет собой соотношение уровня ряда динамики за данный период к его уровню, относящемуся к одному из прошлых периодов. При их исчислении важно обратить внимание на выбор базы сравнения (постоянная или переменная). Относительные величины реализации плана дают количественную характеристику выполнения плановых заданий. Их применение в экономическом анализе обусловлено практикой оперативного и стратегического планирования основных показателей работы фирм, предприятий и организаций. Способы вычисления относительных величин реализации плана зависят от характера показателей выражающих плановое задание. Так, для экономических явлений, которым свойственно поступательное развитие во времени - плановыми заданиями обычно устанавливается достижение в предстоящих периодах тех или иных абсолютных (или средних) Уровней. Относительные величины реализации плана определяются для них как процентное отношение фактически достигнутой в отчетном периоде абсолютной величины к абсолютной величине планового задания. Для некоторых явлений - задания плача предусматривают не рост, а снижение уровней на ту или иную величину. Относительные сравнения фактически достигнутого и запланированного снижения уровня. В экономическом анализе плановое задание может быть выражено и в форме относительной величины, то есть в виде коэффициента рота или прироста уровня в планируемом периоде по сравнению с уровнем базисного периода. В этом случае относительная величина выполнения плана определяемся из процентного сопоставления коэффициента роста явления с плановым коэффициентом. Относительная величина структуры характеризует долю (удельный вес) составных частей целого в их общем итоге и обычно выражается в виде коэффициентов (доли единицы) или процентов. Значение относительных величин структуры в статистике состоит в том, что они применяются для изучения состава (строения) статистической совокупности. Сопоставление структуры явлений, сосуществующих в пространстве, позволяет выявить, особенности их внутреннего строения. Сравнение же структуры явления, развивающегося во времени, позволяет изучить происходящие в явлениях структурные сдвиги (изменения). При определении относительных величин структуры сравниваемыми величинами могут быть или численность отдельных групп статистической совокупности, или объемы признаков. За основание (базу) сравнения принимается общий итог статистической совокупности, то есть при исчислении этих величин важно уяснить их связь с группировкой статистических данных. Примером относительных величин структуры может являться удельный вес мужчин, удельный вес женщин, удельный вес городского, удельный вес сельского населения в общей численности населения и т.д. Если находится соотношение частей целого между собой, то такой вид относительных величин называется координацией. Например, соотношение числа родившихся мальчиков и девочек, соотношение различных видов транспорта по грузооборот и т.д. В статистике часто приходится сопоставлять значения одноименных признаков, но нескольким совокупностям. В результате получают относительные величины сравнения. Например, объем производства молока в Московской области сравнивается с объемом производства в Рязанской области (за одинаковые периоды, например, годы). Относительные величины интенсивности характеризуют степень насыщенности изучаемым явлением определенной сферы. Они выражают соотношение разноименных, но связанных между собой величин и исчисляются как соотношение величин изучаемого явления к объему той среды, в которой происходит развитие явления. Относительные величины интенсивности являются именованными числами и могут выражаться в кратных отношениях, промилле, продецемилле. Так, например, коэффициент фондоотдачи показывает, какой объем валовой продукции приходится на единицу стоимости основных производственных фондов; коэффициент рождаемости показывает, сколько рождений происходит на 1000 человек населения и т.д. При вычислении относительных величин уровня экономического развития, характеризующих размер производства различных видов продукции на душу населения, необходимо годовой объем производства данного вида продукции разделить на среднегодовую численность населения. Средняя величина является важнейшей формой статистического показателя, позволяющей получить обобщенную числовую характеристику статистической совокупности. Основное свойство средней заключается в том. что в ней взаимопогашаются случайные отклонения значений усредняемого признака и проявляется то общее, типичное, что присуще данному объекту в целом. Необходимо учитывать, что средняя только тогда будет являться типичной, когда она рассчитана по однородной совокупности. В противном случае в ней сгладятся не только случайные, но и существенные различия между значением признака у отдельных единиц. Поэтому, если для совокупности условие однородности не выполняется, то общая средняя должна быть •заменена или дополнена средними, рассчитанными по отдельным группам, то есть групповыми средними. При изучении теории средних особое внимание необходимо уделить вопросу правильного выбора средней для каждого конкретного случая. В статистической практике используется средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и степенные средние более высоких порядков. Все степенные средние могут быть либо взвешенными, либо невзвешенными (простыми). Выбор того или иного вида средней базируется на исходном соотношении средней (ИСС), представляющем собой отношение двух экономических категорий, приводящее к искомому среднему показателю. Для каждого конкретного среднего показателя можно составить только одно истинное исходное соотношение, независимо от формы представления исходных данных. Рассмотрим выбор средней на конкретных примерах. Предположим, что распределение работников мастерской по уровню заработной платы характеризуется следующими данными: Таблица 4
Для определения средней заработной платы составим исходное соотношение: Реализуем полученное исходное соотношение: В данном случае мы использовали среднюю арифметическую взвешенную: Если бы значения усредняемого признака не повторялись, тогда достаточно использовать среднюю арифметическую невзвешенную: Определим теперь среднюю урожайность сельскохозяйственной культуры по фермерским хозяйствам области: Таблица 5
Составим исходное соотношение для показателя "Средняя урожайность" Прежде чем приступить к реализации исходного соотношения отметим, что при работе с интервальными рядами распределения необходимо от интервалов перейти к их серединам, при этом величина открытых первого и последнего интервалов условно приравнивается к величине второго и предпоследнего интервалов. В нашем примере середины интервалов будут следующими: 17, 19,21. 23. Реализуем составленное исходное соотношение Рассмотрим следующий пример, в котором, также как и в первом примере, предлагается определить среднюю заработную плату работника в целом по предприятию: Таблица 6
Исходное соотношение для показателя "средняя заработная плата" уже составлено нами в первом примере. При его реализации будем учитывать, что число работников в каждом цехе можно получить делением фонда заработной платы на среднюю заработную плату. Средняя заработная плата по трем цехам: 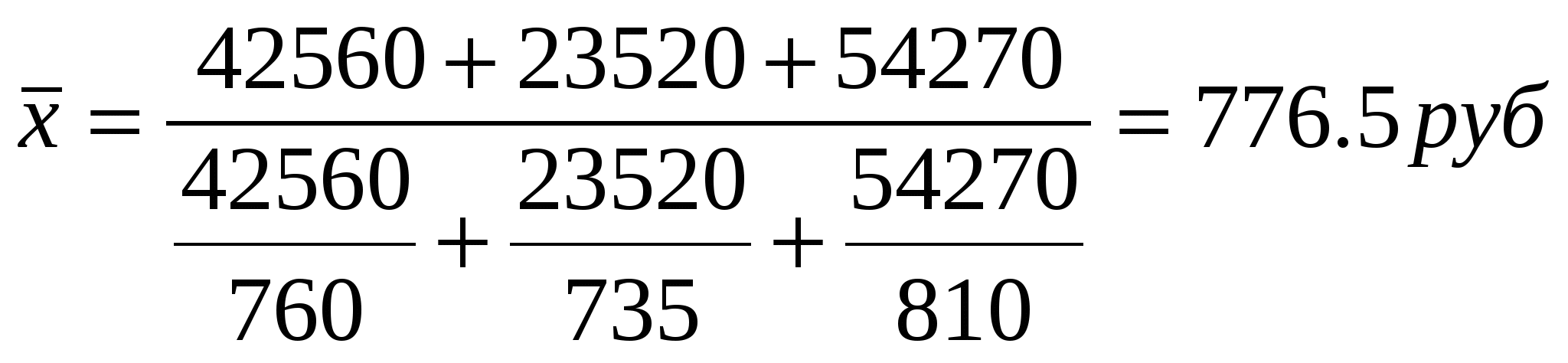 Мы применили среднюю гармоническую взвешенную: С 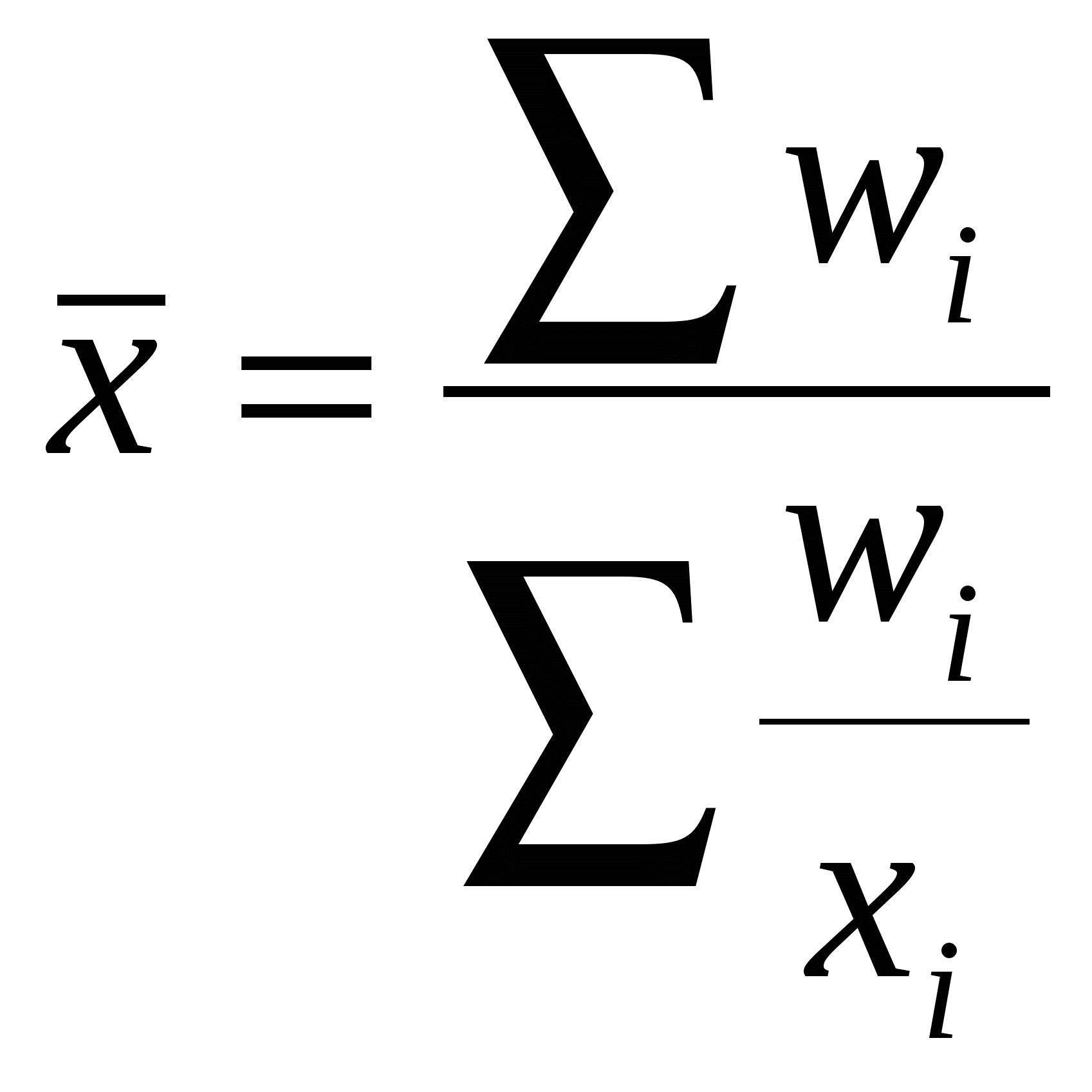 редняя гармоническая простая в расчетах применяется крайне редко. редняя гармоническая простая в расчетах применяется крайне редко.Средняя геометрическая: На использовании средней геометрической базируется показатель среднего темпа роста уровней рядов динамики. Средняя квадратическая и степенные средние более высоких порядков находят применение в ряде расчетных статистических показателей - моментах, показателях вариации и т.п. Помимо степенных средних в статистике применяются так называемые структурные средние, наиболее распространенными среди которых являются мода и медиана. Модой называется вариант признака, имеющий наибольшую частоту. Медиана представляет собой вариант, находящийся в середине ранжированного (упорядоченного) ряда всех значений признака. Вычисление моды (Мо) и медианы (Ме.) различно для дискретных и интервальных рядов. В дискретных рядах мода определяется по наибольшей частоте. Для определения медианы вычисляются накопленные частоты, медианным будет тот вариант, накопленная частота которого первой превысит половину всех частот. Для интервальных вариационных рядов расчет моды и медианы требует применения специальных формул : 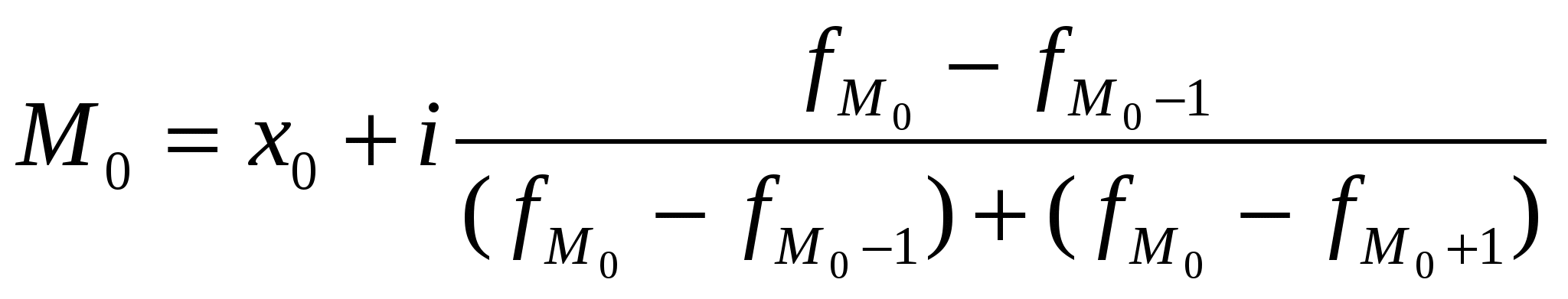 где где 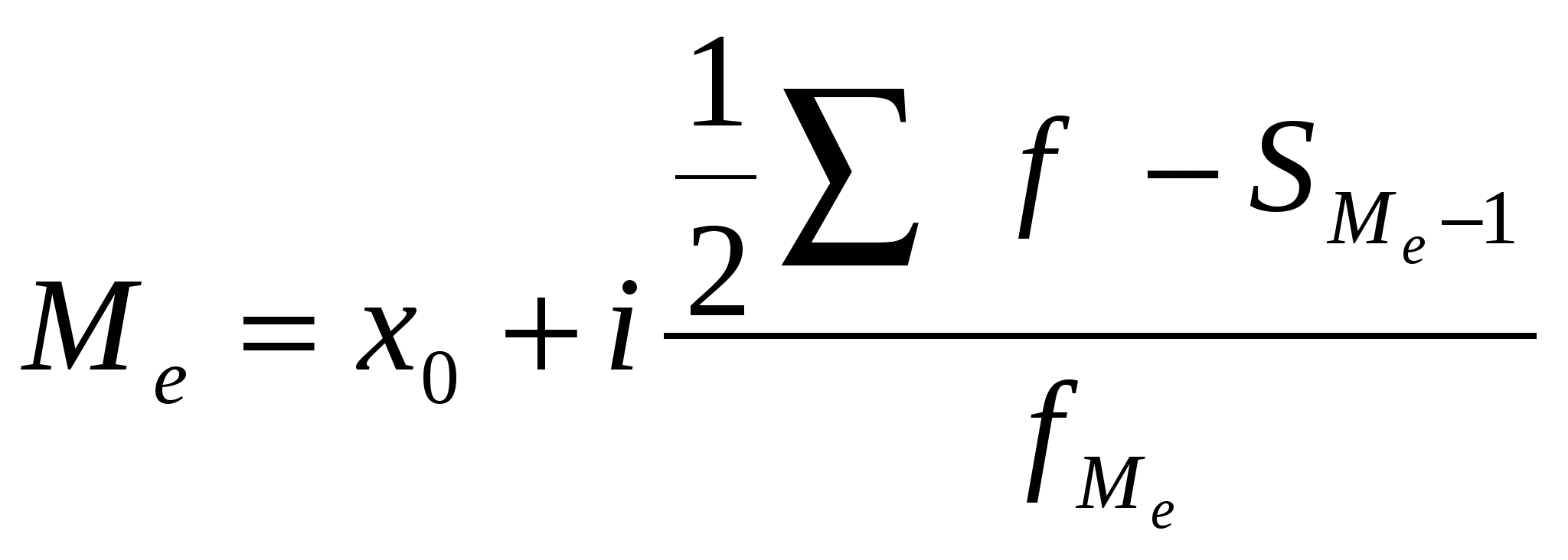 , где , где Определим моду и медиану по следующему ряду распределения: Таблица 7 Распределение торговых предприятий города по размеру среднесуточного товарооборота
Определим моду и медиану: 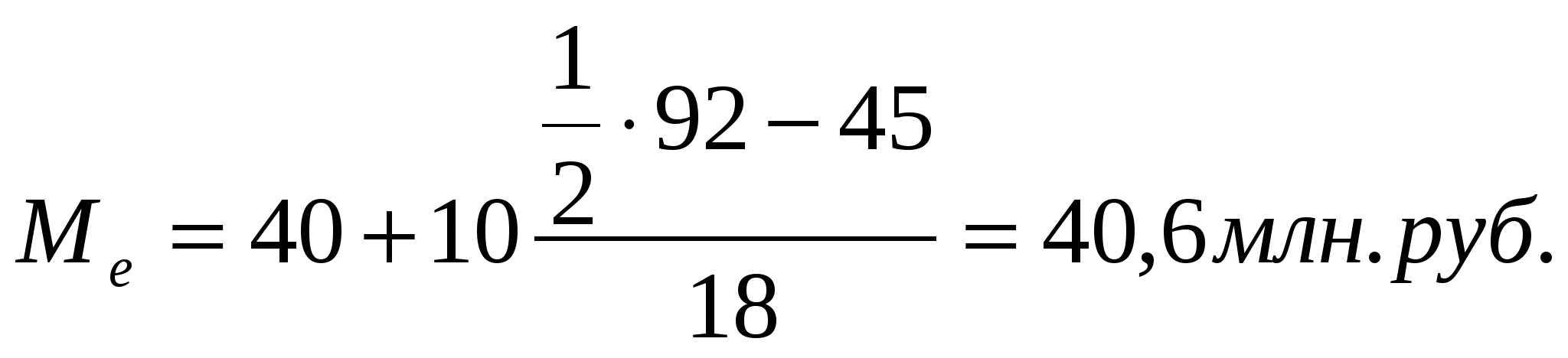 В практике мода и медиана часто используются вместо средней арифметической или наряду с ней. Так, фиксируя средние цены на оптовых рынках, записывают наиболее часто встречающуюся цену каждого продукта, т.е. определяют моду цены. Тем не менее, наилучшей характеристикой величины варианта служит средняя арифметическая, которая имеет ряд существенных преимуществ, главное из которых, точное отражение суммы всех значений признака, использующихся для решения соответствующих практических задач Контрольные вопросы 1.1
Задание для самостоятельной работы Задача 1. По следующим данным определите, в каком семестре уровень успеваемости студентов потока был выше:
Ответ: во 2 семестре средний балл составляет 3.75 против 3,68 в 1 семестре. Задача 2. Имеются следующие данные о дневной реализации помидоров на рынках города:
Вычислите среднюю цену 1 кг помидоров в целом по всем рынкам города. Ответ: 14,0 рублей. Задача 3.Известно распределение работников предприятия по возрасту:
Определите средний возраст работника. Ответ: 42 года. Задача 4. По данным задачи 3 рассчитайте моду и медиану. Ответ: Ми = 33 года, Ме = 42 года. АНАЛИТИЧЕСКАЯ СТАТИСТИКА. ПОКАЗАТЕЛИ ВАРИАЦИИ Методические указания Исследование вариации является составным элементом статистического анализа, позволяющим оценить колебания значений изучаемого признака, однородность совокупности по данному признаку, взаимосвязь его с другими признаками. Показатели вариации служат критерием типичности рассчитанных по совокупности средних величин, используются в определении ошибок выборочных характеристик. При изучении данной темы необходимо обратить особое внимание на расчет основных показателей вариации - дисперсии | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
