Методичка по статистики. Статистическая сводка и группировка. Статистические таблицы
 Скачать 0.79 Mb.
|
 Данный индекс показывает, как изменится средняя цена за счет изменения цен и структуры совокупности. Индекс фиксированного состава показывает только изменение цен и рассчитывается по формуле:  Индекс структурных сдвигов показывает влияние структурных изменений на динамику средней цены. Он рассчитывается по формуле:  Между этими индексами существует следующая взаимосвязь:  Рассмотрим расчет этих индексов на примере. Пример 2. По нижеследующим данным определим общий индекс цен на товар "А" в двух формах: фиксированного и переменного состава, а также оценим влияние структурных сдвигов на динамику средней цены: Таблица 15
Индекс цен переменного состава получается как отношение средней цены двух сравниваемых периодов:  Таким образом, средняя цена товара на двух рынках снизилась на 15,2% во II квартале по сравнению с I кварталом за счет снижения цен и изменения в структуре реализации. Индекс цен фиксированного состава рассчитаем по уже известной формуле:  Таким образом, цена товара на двух рынках снизилась на 7,9% во II квартале по сравнению с I кварталом.  Средняя цена товара снизилась на 8% во II квартале по сравнению с I кварталом за счет изменения структуры реализации. Проверим взаимосвязь:  Контрольные вопросы 1 Дайте определение сводного индекса. 2 Назовите формы сводного индекса. 3 Как связаны между собой цепные и базисные индексы? 4 Как строятся системы индексов с переменными и постоянными весами? 5 Чем отличаются территориальные индексы от динамических? 6 Напишите формулы конкретных индексов, которые Вы знаете. Задания для самостоятельной работы Задача 1. Рассчитайте индексы цен, физического объема товарооборота и товарооборота по следующим данным:
Ответы: 38,4; 113,6 и 100,4. Задача 2. Рассчитайте сводный индекс на основе следующих данных:
Ответ: 101,21%. Задача 3. Рассчитайте общий индекс физического объема продукции по следующим данным:
Ответ: 101%. Задача 4. Рассчитайте индексы производительности труда переменного и фиксированного состава. Определите индекс влияния структурных сдвигов на динамику средней выработки.
Ответ: 120,6%; 114,1%; 105,7%. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ Выборочным называют такое не сплошное наблюдение, при котором обследованию подвергаются не все единицы исследуемой совокупности, а лишь отобранные в определенном порядке. Не прибегая к сплошному обследованию, выборка позволяет получить обобщающие показатели, с той или иной вероятностью отражающие характеристики всей генеральной совокупности При выборочном методе обследованию подвергаются сравнительно небольшая часть всей изучаемой совокупности (5-10% реже 15-25). При этом подлежащая изучению совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная из генеральной совокупности некоторая часть подвергающаяся обследованию, называется выборочной совокупностью. Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность информации, уменьшает ошибки регистрации. В проведении ряда исследований выборочный метод является единственным возможным, например, при контроле качества продукции, если проверка связана с уничтожением или разложением на составные части обследуемых образцов ( определение сахаристости фруктов, клейковины печеного хлеба Следует отметить, что не всякое не сплошное наблюдение может считаться выборкой. Отбор единиц в выборочную совокупность базируется на принципе случайности, при этом заранее определен объем выборки или ее процент, а также выбрана система отбора (способ отбора и метод отбора). Поскольку выборочная совокупность может в той или иной мере отличаться от генеральной, то возникающее расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки. В зависимости от причин возникновения различают ошибки регистрации и ошибки репрезентативности. Ошибки регистрации – это отклонение между значением показателя, полученного в ходе статистического наблюдения, и фактическим, действительным его значением, они. могут быть и при сплошном и при не сплошном наблюдении. Ошибки регистрации бывают случайными, не имеющими какой либо направленности и систематическими, имеющими всегда одну тенденцию – либо к увеличению показателя, либо к уменьшению по каждой единицы совокупности. В отличие от ошибок регистрации ошибки репрезентативности характерны только для не сплошного наблюдения. Они возникают потому, что отобранная совокупность недостаточно точно воспроизводит всю исходную совокупность в целом Ошибки репрезентативности – тоже могут быть случайными и систематическими. Величина случайной ошибки определяет надежность данных выборочного наблюдения, их пригодность для суждения о генеральной совокупности. При помощи формул теории вероятностей можно рассчитать возможную максимальную ошибку. Основными задачами, решаемыми при выборочном наблюдении, являются: а) определение ошибок выборки при известном ее объеме б) определение необходимого объема выборки при заданных максимальных ошибках При изучении темы необходимо разобраться, в чем состоят отличия в решении этих задач при повторном и бесповторном методах отбора, реализуемых собственно-случайным, механическим, типическим или серийным способом.:(бесповторный – отбор, при котором попавшая в выбору единица не возвращается в совокупность, из которой осуществляется дальнейший отбор; повторный – единица после регистрации возвращается в выборку. При этом все единицы совокупности имеют одинаковую вероятности попасть в выборку, т.к. совокупность остается неизменной. Следует иметь ввиду, что при любой системе отбора выборочный метод позволяет получить не точечные, а интервальные характеристики генеральной совокупности при заданном уровне вероятности. При этом в качестве генеральной характеристики может выступать генеральная средняя  , т.е. среднее значение признака во всей изучаемой совокупности, или генеральная доля p, т.е. доля единиц, обладающих тем или иным значением признака. Особенность выборочного обследования в состоит в том, что на основе характеристик выборочной совокупности (частность w, , средняя  ) получить достоверные суждения о показателях доли p или в генеральной совокупностиРассмотрим решение типовых задач по выборке. Задача 1. В результате выборочного наблюдения затрат времени на изготовление некоторых деталей получены следующие данные: Таблица 16
Требуется: 1. Определить выборочные характеристики: средние затраты времени на изготовление одной детали и долю деталей, на которые затрачивается до 24 мин. 2. Вычислить средние ошибки этих показателей. 3. Рассчитать с вероятностью 0,954 предельные ошибки.и границы нахождения генеральных характеристик. Решение. На основе ряда распределения определим требуемые характеристики: 1) средние затраты времени на изготовление одной детали:  2) доля деталей, на которые затрачивается до 24 мин.:  3) средние ошибки полученных характеристик определим по формулам собственно-случайного повторного отбора, так как доля выборки у нас незначительна и поправка на бесповторность отбора существенно не повлияет на результат:  ;  Соответствующие дисперсии равны   Тогда  ( для средней) (для доли)4) переход от средней (  ) к предельной ( ) ошибке осуществляется по формуле  (для всех видов выборки "t" -величина, связанная с вероятностью, с которой гарантируется результат). У нас Р = 0,954. Ей соответствует значение t = 2. Тогда имеем   Отсюда с вероятностью 0.954 можно указать границы для генеральных характеристик:  или   или  Задача 2. По данным задачи N1 определить предельные ошибки выборочных показателей с той же вероятностью при условии 20- процентного бесповторного отбора: 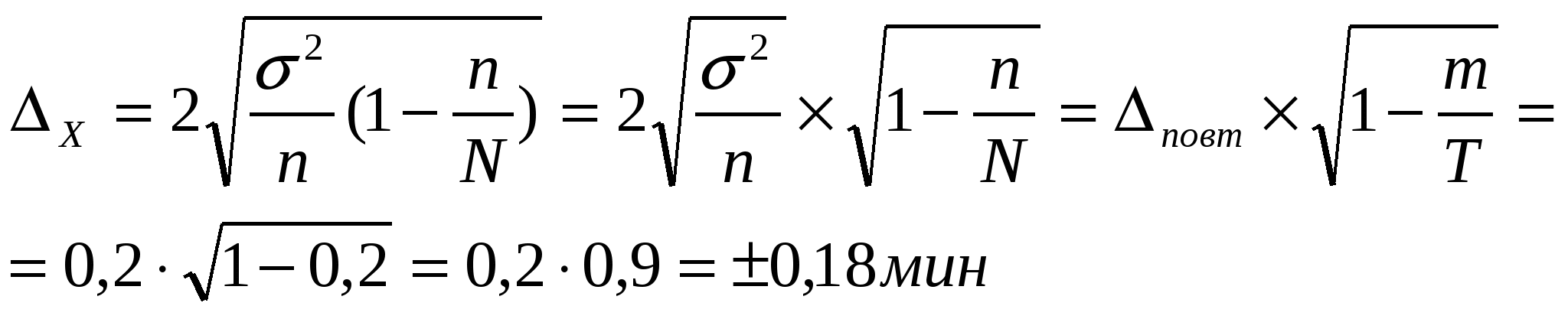  Задача 3. Сколько деталей необходимо отобрать из партии в 2000 штук в порядке бесповторного отбора, чтобы ошибка средних затрат времени на изготовление деталей не превышала 0,2 мин., а ошибка доли деталей, на изготовление которых тратится менее 24 мин. - 4%, с вероятностью 0,95.   Примечание: необходимые для расчетов дисперсии взяты из первой задачи. Оценка дисперсии при определении объема выборки является наиболее трудной проблемой планирования выборочного наблюдения При контроле качества товаров в экономических исследованиях эксперимент может проводиться на основе малой выборки. Под малой выборкой понимается несплошное статистическое обследование, при котором совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем обычно не более 30 единиц, а может доходить до 4-5. В торговле к минимальному объему выборки прибегают, когда большая выбока или невозможна, или нецелесообразна ( порча или уничтожение образцов). Средняя ошибка малой выборки  , где,  (вычисление дисперсии малой выборки происходит с участием числа степеней свободы.)Под числом степеней свободы понимается количество вариантов, которые могут принимать произвольные значения, не меняя средней. Предельная ошибка малой выборки -  . При этом значение коэффициента доверия t зависит не только от заданной доверительной вероятности, но и от численности выборки n. . Для определения вероятности используют таблицы Стьюдента. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||