Методичка по статистики. Статистическая сводка и группировка. Статистические таблицы
 Скачать 0.79 Mb.
|
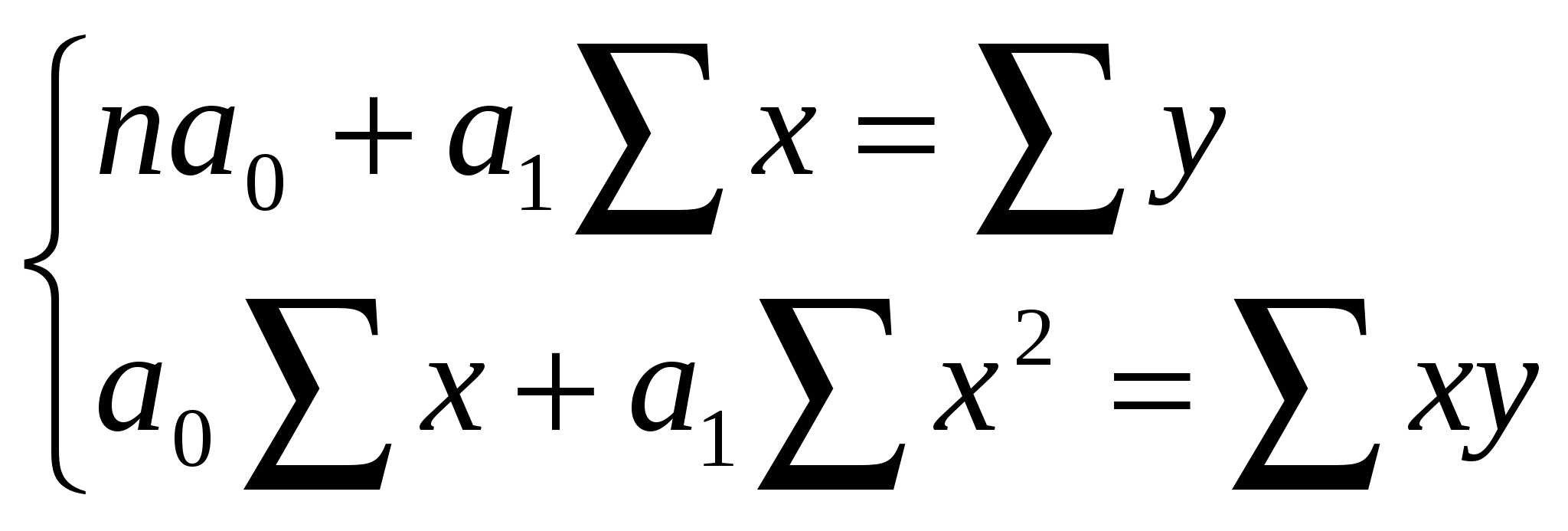 , где  - выравненные (теоретические) значения результативного признака (ставка); - факторный признак (срок выдачи кредита); - параметры уравнения регрессии.Параметры находят из системы нормальных уравнений  Тесноту связи в случае линейной зависимости определяют на основе линейного коэффициента корреляции К.Пирсона:  Средние квадратические отклонения можно рассчитать по следующим формулам  и  В следующей таблице приведены необходимые предварительные вычисления (последняя строка содержит средние значения): Исходные и расчетные данные по сроку выдачи кредитов и процентной ставке Таблица 1
Подставив из таблицы в систему нормальных уравнений необходимые итоги, получим: 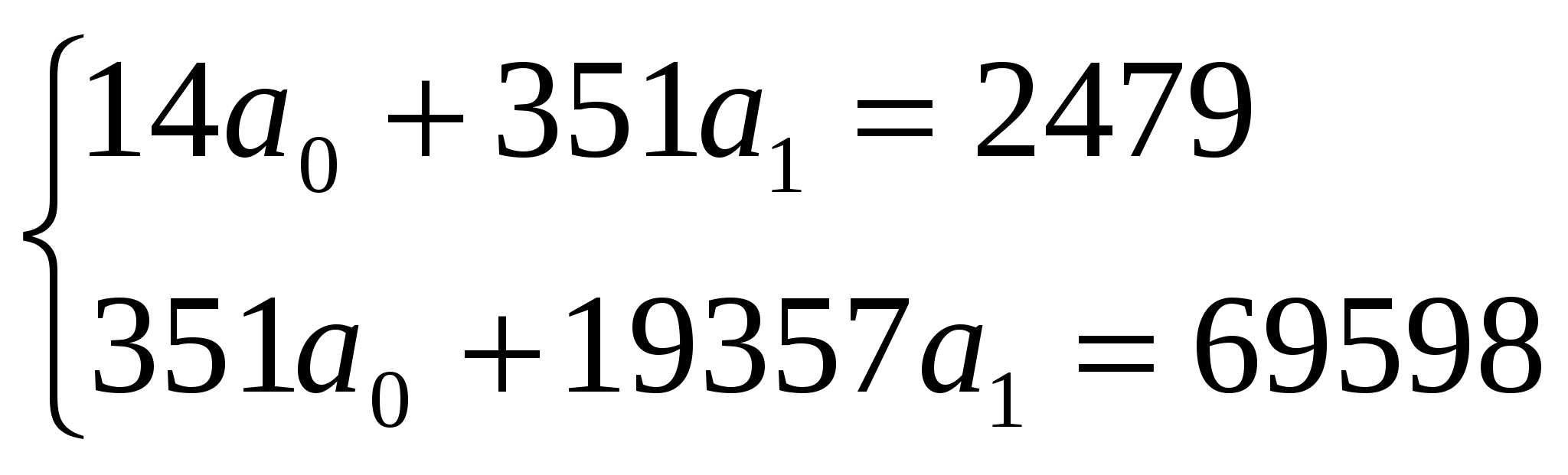 Решив эту систему, найдем:  =143,23 и  =1,35С учетом этого искомое уравнение регрессии имеет следующий вид:  Интерпретация данного уравнения сводится к следующему: с увеличением срока выдачи кредита на 1 день процентная ставка в среднем возрастает на 1,35%. Подставляя в это уравнение последовательно все значения факторного признака определяем теоретические значения результативного признака  (см. последнюю графу приведенной выше таблицы). Необходимым, но не достаточным условием правильности расчетов является равенство сумм фактических и теоретических значений результативного признака.Определение величины линейного коэффициента корреляции начнем с расчета средних квадратических отклонений:  и  С учетом рассчитанных значений получим:  Линейный коэффициент корреляции изменяется в пределах от-1 до +1. При этом знак указывает на направление связи, а величина коэффициента, взятая по модулю - на тесноту связи. Рассчитанный нами коэффициент указывает на прямую тесную зависимость между сроком выдачи кредита и процентной ставкой. При изучении нелинейных зависимостей особое внимание необходимо обратить на оценку тесноты связи с помощью теоретического корреляционного отношения, так как линейный коэффициент корреляции здесь непригоден. Множественный корреляционно-регрессионный анализ возможен только с использованием компьютера. Однако необходимо уметь анализировать матрицу парных коэффициентов корреляции на наличие мультиколлинеарности и понимать смысл множественного и частных коэффициентов корреляции. Завершить изучение данной темы мы рекомендуем рассмотрением показателей тесноты связи между альтернативными признаками (коэффициенты ассоциации и контингенции) и между атрибутивными признаками (коэффициенты взаимной сопряженности Чупрова и Пирсона), а также рассмотрением ранговых коэффициентов корреляции Спирмена и Кэндала. Контрольные вопрос
Задание для самостоятельной работы Задача 1. По данным о ценах на молоко и сметану на рынках десяти российских городов постройте линейное уравнение регрессии и оцените тесноту связи:
Ответ:   СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для ее отражения строятся ряды динамики. Особое внимание следует обратить на условия сопоставимости данных, составляющих динамический ряд. При рассмотрении вопросов о видах рядов динамики надо, прежде всего, понять различие между моментными и интервальными рядами. Построение, обработка и анализ этих рядов во многом определяется их особенностями. Затем следует перейти к изучению методов расчета аналитических показателей рядов динамики. В настоящей теме эти показатели должны быть рассмотрены вместе другими показателями анализа рядов динамики. Следует учесть при этом, что анализ относительных показателей должен изводиться во взаимосвязи с анализом абсолютных величин (уровней ряда, абсолютных приростов). С этой точки зрения большое значение имеет исследование абсолютного значения одного процента прироста. Рассчитывая аналитические показатели ряда динамики, необходимо правильно выбирать базу для сравнения. Этому вопросу следует уделить особое внимание. Необходимо также разобраться в способах получения средних величин ряда: среднего уровня, среднего абсолютного прироста, среднего темпа роста и прироста. Следует помнить, что способ расчета среднего уровня ряда динамики зависит от его вида. При расчете среднего темпа роста необходимо использовать среднюю геометрическую. При изучении вопросов выявления тенденции ряда динамики необходимо уяснить такие методы выявления тенденции ряда динамики как укрупнение интервала, сглаживание способом скользящих средних, аналитическое выравнивание. Рассмотрим для примера расчет аналитических показателей ,а динамики по следующим данным: Таблица 12 Число зарегистрированных крестьянских (фермерских) хозяйств в Российской Федерации
На основе этих данных необходимо рассчитать абсолютные приросты. темпы роста и прироста, средний уровень ряда, средний темп роста и прироста, а также абсолютное значение одного процента прироста. Для расчета абсолютного прироста необходимо из уровня каждого последующего года вычесть уровень предыдущего или начального года (или какого-либо другого, принятого за базу сравнения). Так, например, абсолютный прирост в 1995г. по сравнению с 1994г. составил 279,2-270,0=9,2тыс.,а по сравнению с начальным - 1991г. 279,2-4,4 = 274,8тыс. Темп роста представляет собой отношение уровня последующего года к уровню предыдущего или начального. Так для 1995г. темп роста по сравнению с 1994г. составил (279,2:270,0)-100 = 103,4%, а по сравнению с 1991 г. (279,2:4,4) • 100 = 634,5% . Темп прироста есть отношение абсолютного прироста к предыдущему или начальному уровню (или какому-либо другому, принятому за базу сравнения). Для 1995г. по сравнению с 1994г. темп роста равен (9,2:270,0)-100=3,4% или 103,4-100=3,4%. Абсолютное значение одного процента прироста получается в результате деления абсолютного прироста по сравнению с предыдущим периодом на соответствующий темп роста, выраженный в процентах. Приведем в таблице результат расчета всех этих показателей анализа ряда динамики (Табл.13). Рассчитаем также средние показатели. Средний уровень ряда динамики числа фермерских хозяйств рассчитывается по формуле средней арифметической простой, поскольку данный ряд интервальный:  Столь же просто находится средний абсолютный прирост:  Для расчета среднего темпа роста используем среднюю геометрическую:  или 100,9%Следующей проблемой изучения динамики является выявление основной тенденции, то есть главного направления в изменении изучаемого явления. Речь идет о случаях скрытой тенденции, присущей тому или иному ряду динамику. Например, за колебаниями уровней урожайности какой-либо сельскохозяйственной культуры в отдельные годы тенденция роста урожайности может не просматриваться непосредственно, и поэтому должна быть выявлена статистически. Из различных методов выявления тенденции, обычно рассматриваемых в учебной литературе (укрупнение интервалов, механическое сглаживание, аналитическое выравнивание), обратите особое внимание на последний. Необходимо учитывать, что аналитическое выравнивание представляет собой частный случай применения метода регрессии к анализу социально-экономических явлений. Этот метод заключается в том, что уровни ряда динамики представляются как функция времени (t):  Таблица 13
В качестве примера произведем выравнивание данных о выплавке чугуна по уравнению прямой | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
