Методичка по статистики. Статистическая сводка и группировка. Статистические таблицы
 Скачать 0.79 Mb.
|
 ,среднего квадратического отклонения  среднего линейного отклонения , коэффициента вариации ( ) - по первичным и сгруппированным данным (рядам распределения). Во втором случае применяются не простые, а взвешенные формулы соответствующих показателей.Рассмотрим вычисление показателей вариации на следующем примере: Таблица 8 Распределение предприятий торговли района по размеру торговой площади
Заполнению последних четырех граф данной таблицы предшествовал расчет средней величины изучаемого признака, выполненный по формуле средней арифметической взвешенной:  Вычислим показатели вариации:     Статистическую совокупность можно считать однородной по рассматриваемому признаку, если коэффициент вариации не превышает 33%. Таким образом, исследуемая совокупность является неоднородной, поэтому при рассмотрении исходных данных необходимо решить вопрос об исключении аномальных наблюдений (если такие имеются) или разбить совокупность на несколько групп, а затем определить показатели вариации у вновь образованных совокупностей. При формулировке выводов о степени вариации следует обратить внимание на то, что коэффициент вариации является относительной мерой колеблемости и может приводить к результатам, противоположным полученным на основе абсолютных показателей вариации. Так. например, если в первом цехе дисперсия выработки деталей работниками  =9 при средней выработке  -140, а во втором цехе эти показатели соответственно  =11 и  =170, то абсолютная вариация будет сильнее во втором цехе ( ), а относительная в первом  и  Наибольшую трудность в изучении данной темы представляет расчет общей дисперсии по правилу сложения дисперсий:   , где  - средняя из внутригрупповых дисперсий  ,а  -межгрупповая дисперсия,  , где  и  - соответственно групповые средние и численности по отдельным группам;Правило сложения дисперсий может быть применимо только в том случае, когда совокупность разбита на две или более группы по какому-либо факторному признаку, предположительно оказывающему влияние на вариацию исследуемого признака. Вариация признака внутри групп определяется воздействием всех прочих факторов и отражается в величине средней из внутригрупповых дисперсий. Тесноту связи между факторным и результативным признаками оценивают с помощью эмпирического корреляционного отношения 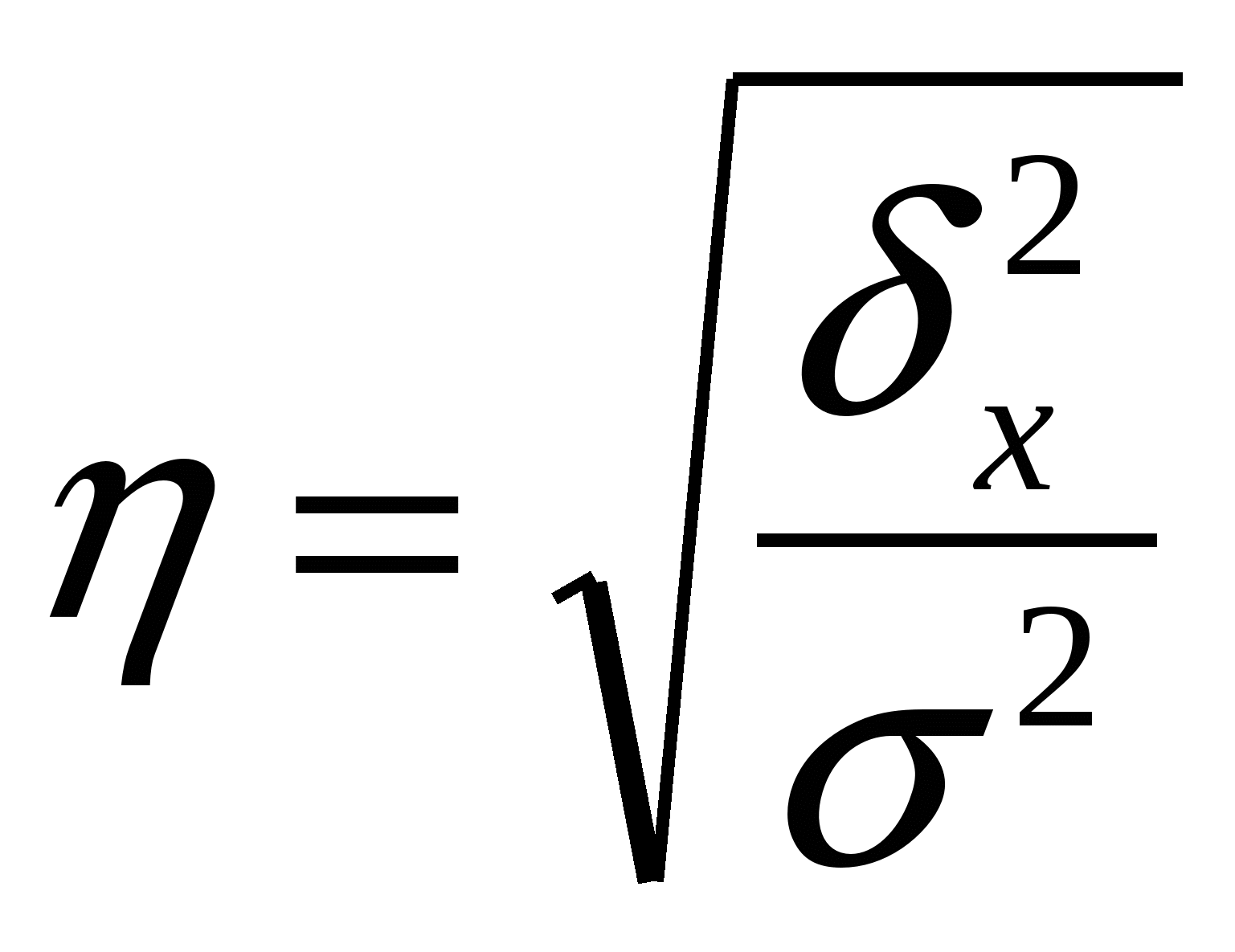 . Данный показатель может принимать значения от 0 до I .В статистическом анализе широко используется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии -эмпирический коэффициент детерминации  , он показывает долю (удельный вес) общей вариации изучаемого признака, обусловленного вариацией группировочного признака.На следующем условном примере исследуем зависимость между собственными и привлеченными средствами коммерческих банков региона: Таблица 9
Произведем группировку банков, выделив две группы по величине собственных средств: до 100 млн. руб. и свыше 100 млн. руб., и проанализируем влияние данного группировочного признака (фактора) на размер привлеченных средств. Первая группа объединит коммерческие банки N-N 1, 2, 5, 7, 8, 9, во вторую группу войдут N-N 3, 4, 6. 10. Расчет эмпирического корреляционного отношения состоит из нескольких этапов: 1) рассчитываем групповые средние и общую среднюю по результативному признаку - привлеченные средства (i - номер группы,] 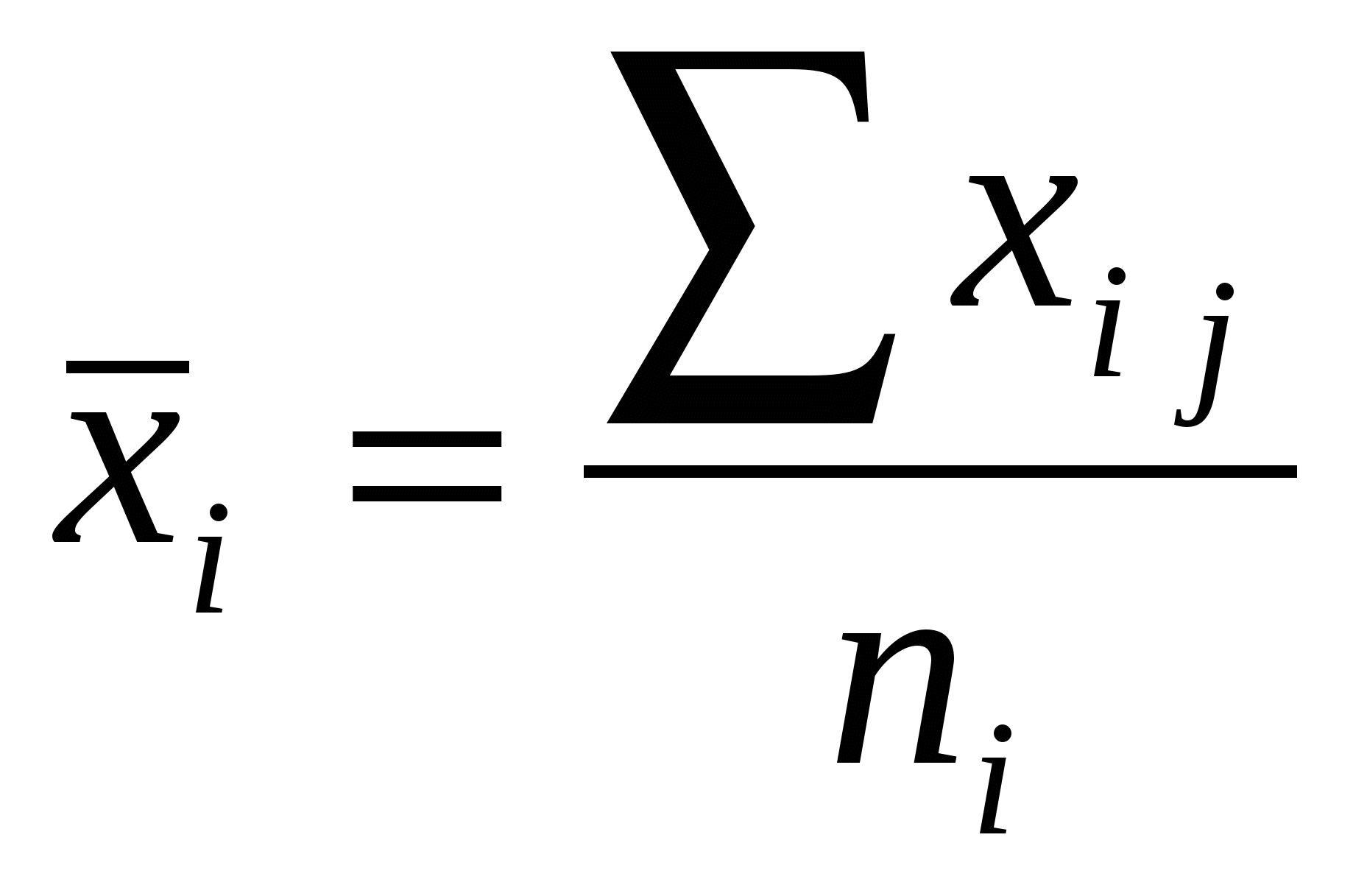 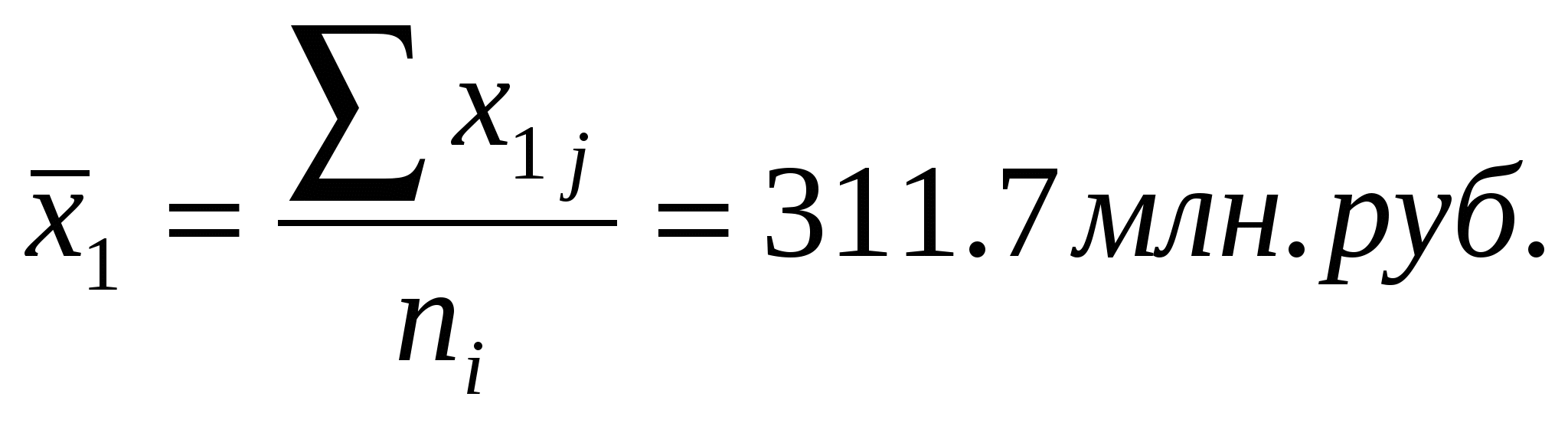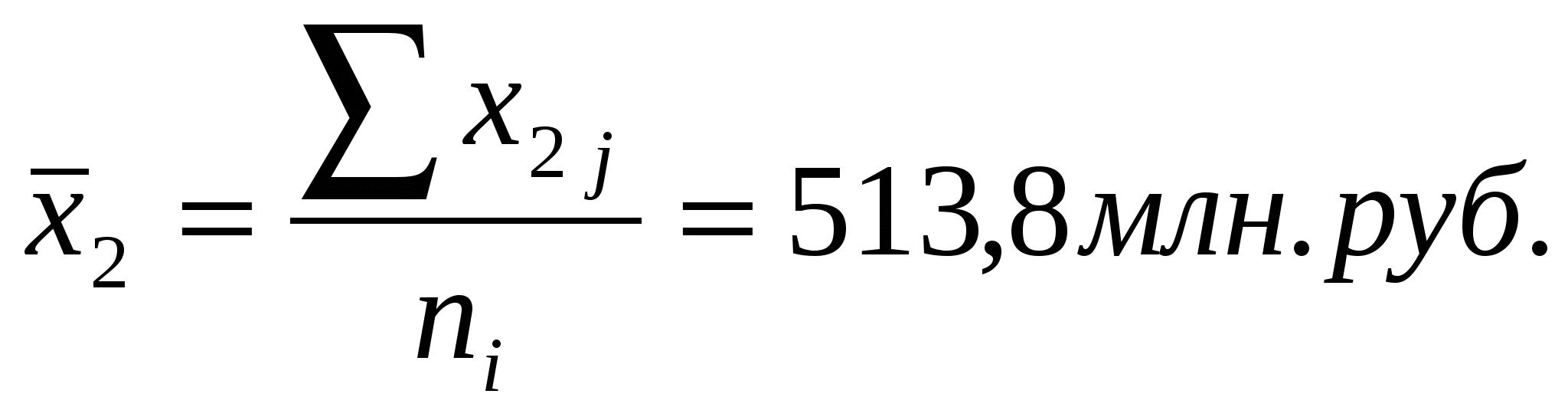- номер единицы в группе):     2) рассчитываем внутригрупповые дисперсии:   3) вычисляем среднюю из внутригрупповых дисперсий:  4)определяем межгрупповую дисперсию:  5) Находим общую дисперсию по правилу сложения  6)рассчитываем эмпирическое корреляционное отношение: 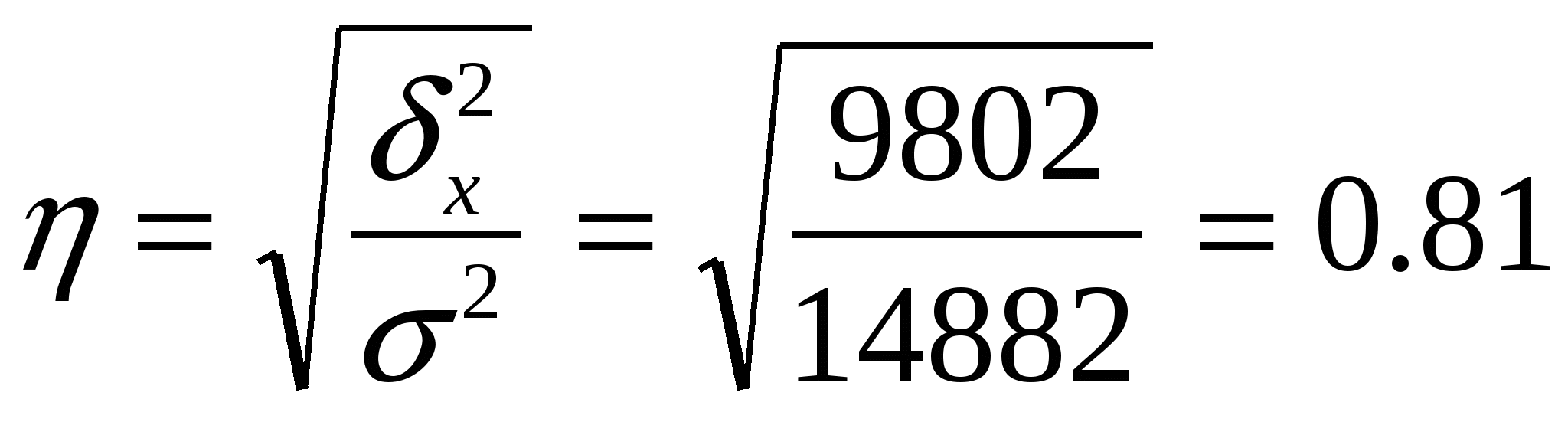 Полученная величина свидетельствует о том, что фактор, положенный в основание группировки (собственные средства), существенно влияет на размер привлеченных средств Дисперсия альтернативного признака. Альтернативные признаки – признаки, которыми обладают одни единицы совокупности и не обладают другие. (Работники торговли подразделяются на мужчин и женщин, т.е. в данном случае это взаимоисключающие варианты.) Если возникает необходимость измерить вариацию альтернативного признака, то применяют следующее обозначение: 1- если интересующий нас признак в наличие ; 0 – если данный признак отсутствует.; долю единиц, обладающих данным признаком -p ; долю единиц не обладающим признаком -q . Среднее значение альтернативного признака  , т.к. p+q=1 (сумма долей, обладающих и не обладающих признакам равна единице) Дисперсия альтернативного признака:  , т.к.  , т.к. p+q=1 подставим вместо 1-p – q  Т.О. дисперсия альтернативного признака равна произведению доли единиц обладающих данным признаком и доли единиц им не обладающих. Контрольные вопросы
Задание для самостоятельной работы Задача 1. В целях контроля качества выпускаемых предприятием электроламп на стенде выполнены замеры продолжительности горения 500 ламп, которые привели к следующим результатам:
Определите: 1) размах вариации; 2) дисперсию; 3) среднее квадратическое отклонение; 4) среднее линейное отклонение; 5) коэффициент вариации. Ответы: 1)500 ч.; 2) 13980;3) 118 ч.; 4) 97 ч.; 5) 6,1%. Задача 2. С помощью эмпирического корреляционного отношения оцените взаимосвязь между возрастом и числом дней временной нетрудоспособности работников предприятия:
Ответ:  =28,6;  =91,8;  =0,558СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ Методические указания Изучение данной темы целесообразно начать с рассмотрения классификации статистических связей по различным классификационным признакам. Далее необходимо познакомиться с простейшими приемами выявления и анализа взаимосвязей -приведением параллельных данных и построением поля корреляции. Следует также обратить внимание на метод аналитических группировок, позволяющий проследить взаимозависимость не только между количественными, но и между качественными признаками. Наибольшую трудность для усвоения представляет метод корреляционно-регрессионного анализа. Изучая его, целесообразно придерживаться такой последовательности: 1. Линейная регрессия. 2. Нелинейная регрессия. 3. Множественная регрессия. Применение корреляционно-регрессионного анализа требует наличия следующих условий: - независимость наблюдений; -отсутствие тесной зависимости между факторными признаками; - наличие достаточного объема наблюдений; -соответствие формы уравнения регрессии характеру взаимосвязи. Поэтому методу корреляции и регрессии всегда предшествует качественный анализ. Рассмотрим пример построения линейного уравнения регрессии и оценки тесноты связи. Исследуем связь между сроком выдачи кредитов одного и того же объема и процентной ставкой по итогам торгов на аукционе: Таблица 10
Предположим, что зависимость здесь линейная: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
