Статистика - лекция - Корреляция. Статистическое изучение взаимосвязи социальноэкономических явлений. Корреляционнорегрессионный анализ
 Скачать 0.86 Mb.
|
|
ТЕМА: «Статистическое изучение взаимосвязи социально-экономических явлений. Корреляционно-регрессионный анализ».
1. Причинность, регрессия, корреляция. Исследование объективно существующих связей между явлениями – важнейшая задача теории статистики. Связи между признаками и явлениями, ввиду их большого разнообразия, классифицируются по ряду оснований. Признаки по их значению для изучения взаимосвязи делятся на два класса. Признаки, обусловливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называют результативными. Из множества разнообразных форм проявления взаимосвязей в качестве двух самых общих видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно и только одно значение результативного признака. Корреляционная связь проявляется в среднем для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Связи между явлениями и их признаками классифицируются по степени тесноты, по направлению и по аналитическому выражению. По степени тесноты связи различают количественные критерии оценки тесноты связи (в соответствии со шкалой Чеддока, о чём речь пойдёт в дальнейшем). По направлению связи бывают прямыми и обратными, положительными и отрицательными. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. Например, увеличение степени механизации труда способствует росту рентабельности строительного производства. В случае обратной связи значения результативного признака изменяются в противоположном направлении по сравнению с изменением факторного признака. Так, с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции. Относительно своей аналитической формы связи могут быть линейные и нелинейные. Если статистическая связь между явлениями приближенно выражена уравнением прямой линии, то её называют линейной связью; если же она выражена уравнением какой – либо кривой линии (параболы, гиперболы: степенной, показательной и т. д.), то такую связь называют нелинейной или криволинейной. Для выявления наличия связи, ее характера и направления используют методы: приведения параллельных данных, аналитических группировок, графический, корреляции. Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению ожидания другой. В статистике принято различать следующие варианты зависимостей: 1. Парная корреляция – связь между признаками (результативным и факторным признаками или двумя факторными). 2. Частная корреляция - зависимость между результативным и факторным признаками при фиксированном значении других факторных признаков. 3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.
регрессия. Корреляционно-регрессионный анализ включает в себя измерение тесноты, направление связи и установление аналитического выражения связи. Одним из методов корреляционно-регрессионного анализа является метод парной корреляции, рассматривающий влияние вариации факторного признака Х на результативный У. Аналитическая связь между ними описывается уравнениями: прямой  параболы  гиперболы  Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о наличии линейной связи между ними, а при обратной связи – гиперболической. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная функции. Оценка параметров уравнения регрессии ао и а1 осуществляется методом наименьших квадратов, в основе которого лежит требование минимальности сумм квадратов отклонений эмпирических данных Yi от выровненных (теоретических)  : min(1)Система нормальных уравнений для нахождения параметров линейной парной регрессии имеет вид: 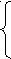  (2) Для оценки типичности параметров уравнения регрессии используется t – критерий Стьюдента. При этом вычисляются значения t- критерия: для параметра   (3)для параметра   (4)В формулах (3) и (4): 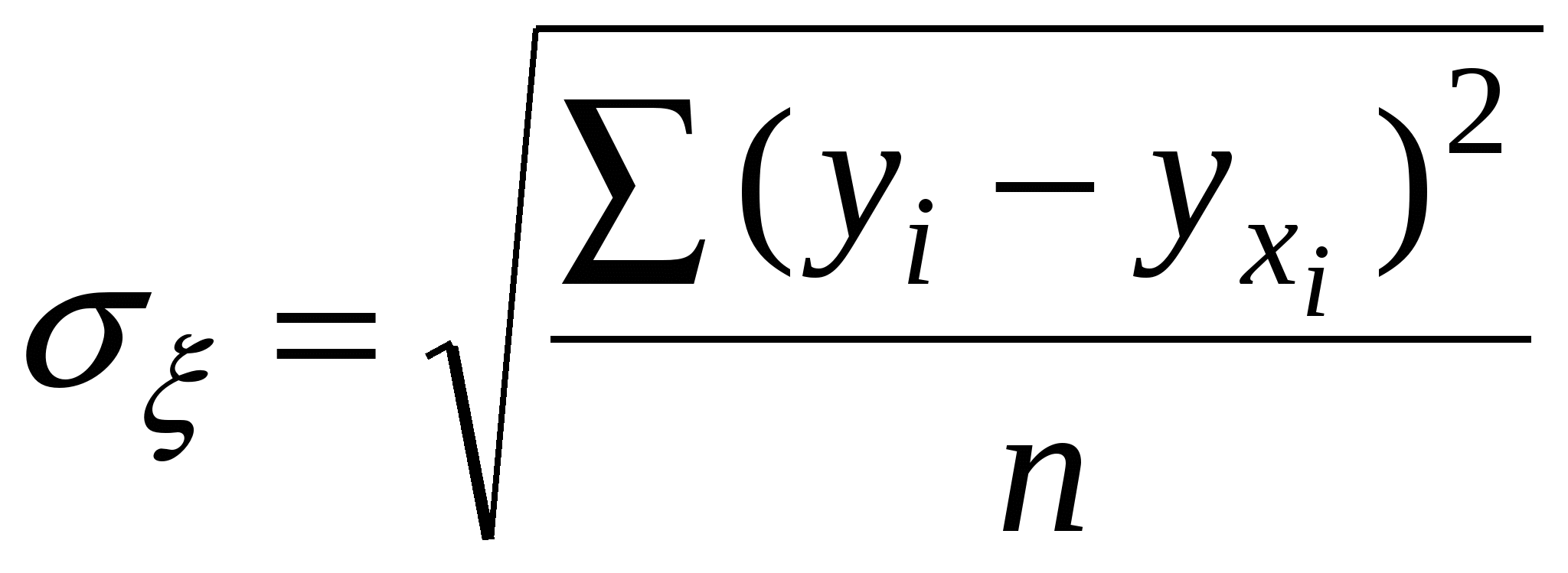 (5)σξ - среднее квадратическое отклонение результативного признака  от выровненных значений : (6) σX - среднее квадратическое отклонение факторного признака  от общей средней  .Полученные по формулам (3) и (4) фактические значения  и  сравниваются с критическим  , который получают по таблице Стьюдента с учетом принятого уровня значимости  и числа степеней свободы  .Полученные при анализе корреляционной связи параметры уравнения регрессии признаются типичными, если t фактическое больше t критического  (7)По проверенным на типичность параметрам уравнения регрессии производится построение математической модели связи. При этом параметры примененной в анализе математической функции получают соответствующие количественные значения: параметр а0 показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр а1 – на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения. Проверка практической значимости синтезированных в корреляционно-регрессивном анализе математических моделей осуществляется посредством показателей тесноты связи между признаками х и у. Для статистической оценки тесноты связи применяются следующие показатели вариации:
 (8)
 (9)Формула (9) характеризует отклонение выровненных значений  от их общей средней величины  ;
 (10)Формула (10) характеризует отклонения эмпирических (фактических) значений результативного признака yi от их выровненных значений .Соотношение между факторной и общей дисперсиями характеризует меру тесноты связи между признаками x и y 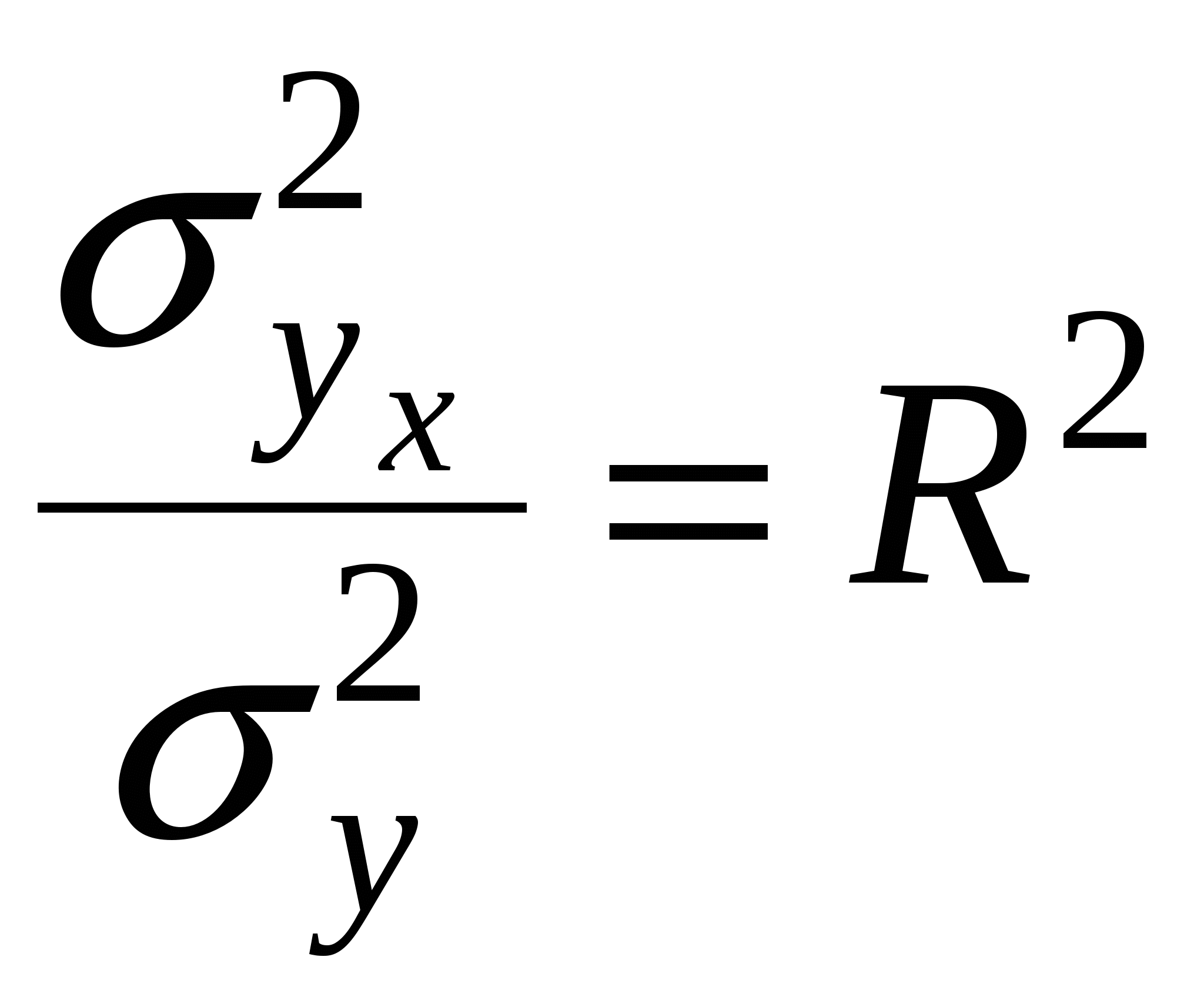 (11)Показатель R2 называется индексом детерминации (причинности). Он выражает долю факторной дисперсии, т.е. характеризует, какая часть общей вариации результативного признака y объясняется изменением факторного признака x. На основе формулы (11) определяется индекс корреляции R 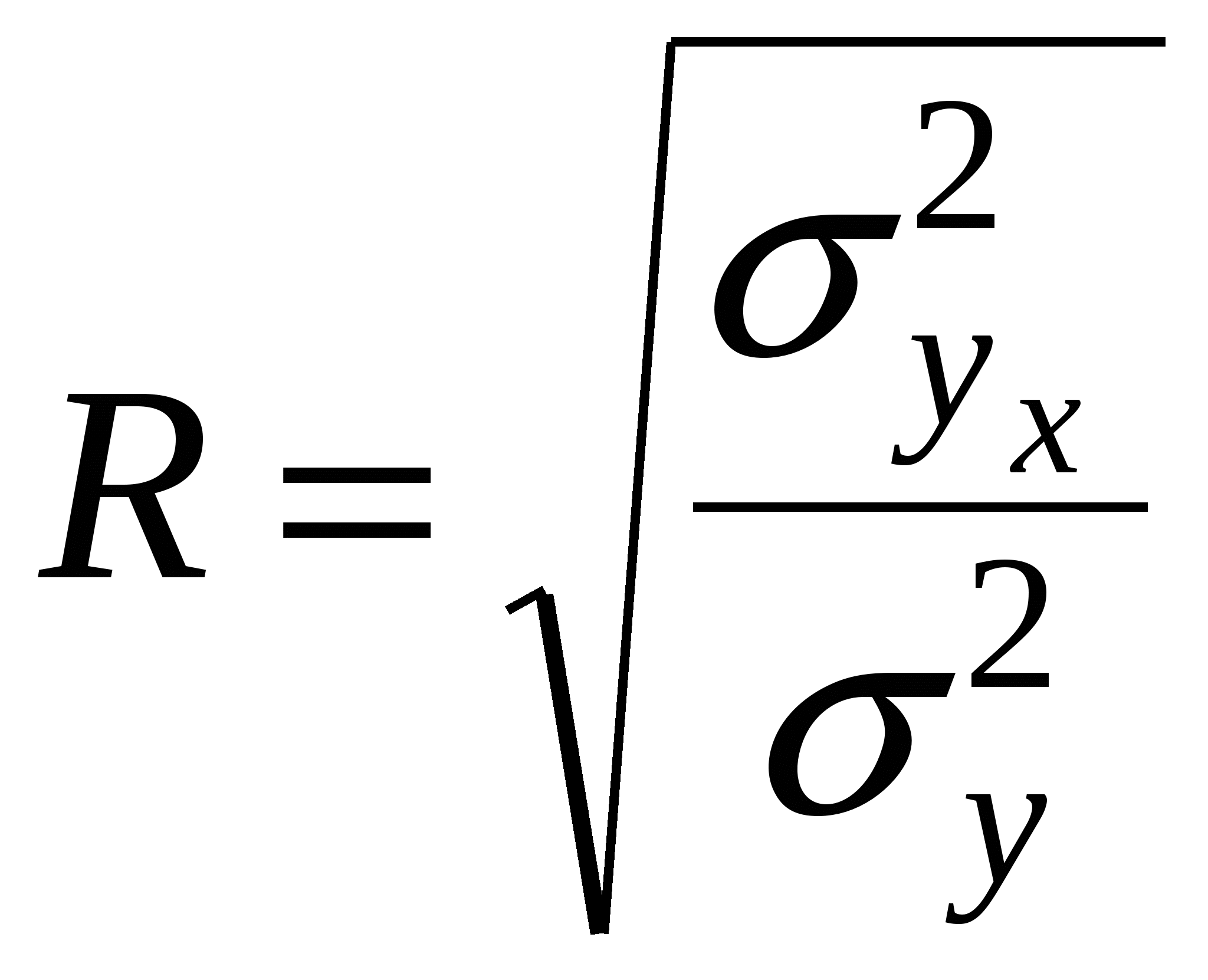 (12)Используя правило сложения дисперсии, получают формулу индекса корреляции 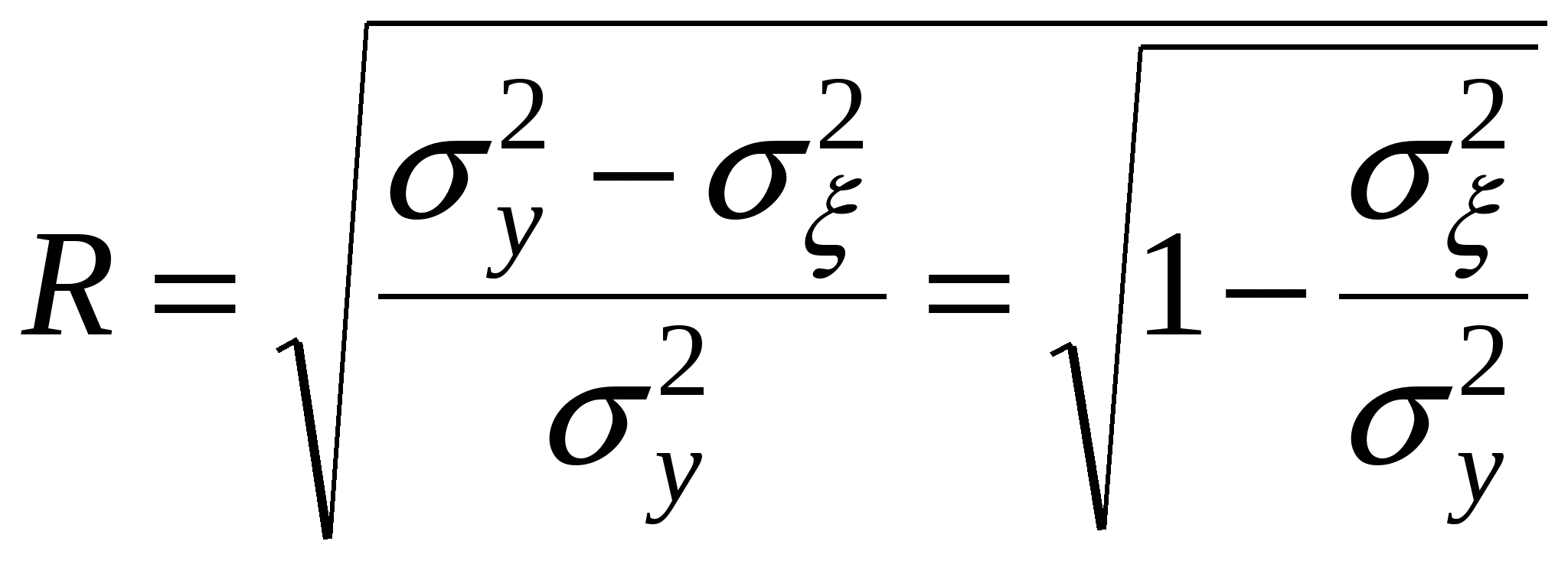 (13)Формула (71) является основным алгоритмом для определения индекса корреляции с использованием машинной обработки анализируемых данных. При прямолинейной форме связи показатель тесноты связи определяется по формуле линейного коэффициента корреляции r. В теории разработаны и на практике применяются различные модификации формулы расчёта данного коэффициента:  , где 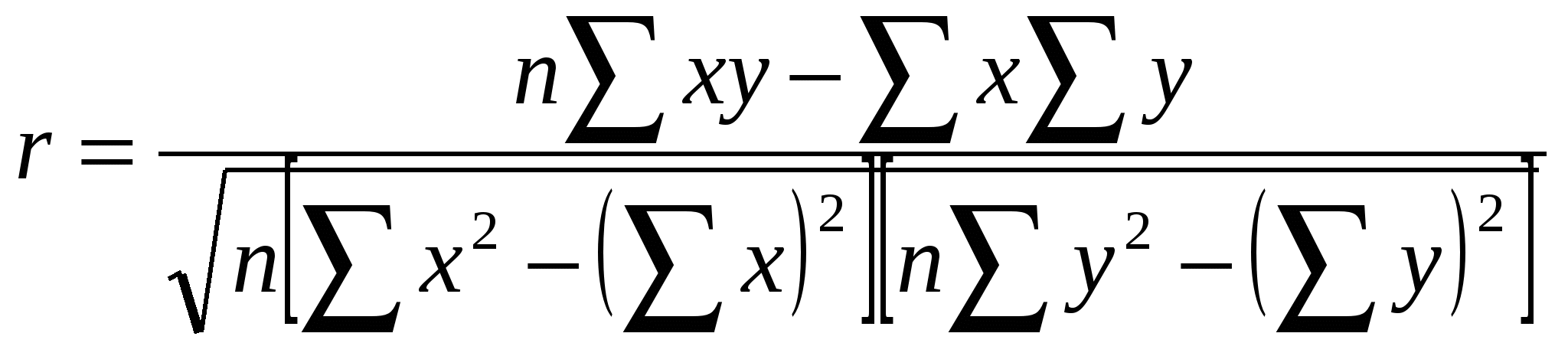  или  или 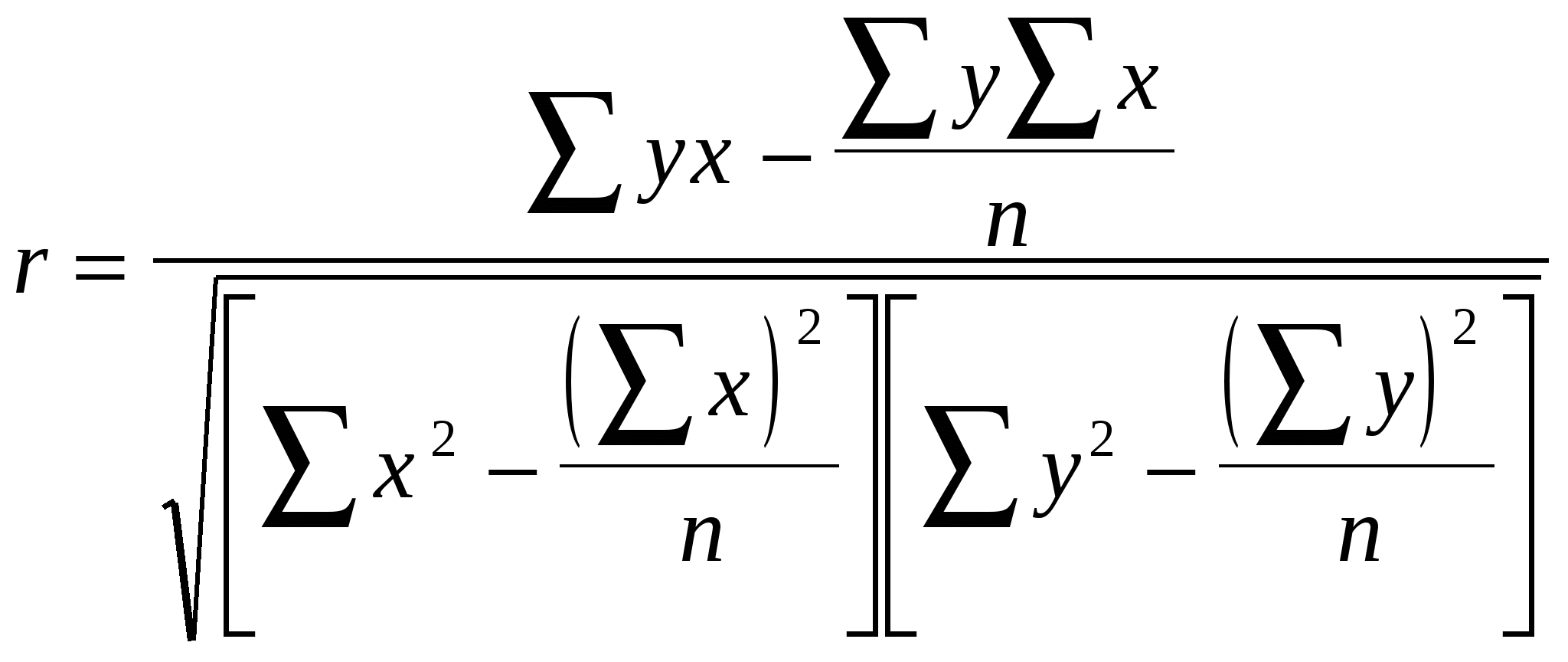 (14)Заметим, что по абсолютной величине линейный коэффициент корреляции r равен индексу корреляции r только при прямолинейной связи. Линейный коэффициент корреляции изменяется в пределах от -1 до 1: -1 ≤ r ≤ 1. Знаки коэффициентов регрессии корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно представить в следующей таблице: Оценка линейного коэффициента корреляции
Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности. Для оценки значимости коэффициента корреляции r применяется t-критерий Стьюдента. При этом определяется фактическое значение критерия tr  (15)Вычисленное по формуле (15) значение tr сравнивается с критическим tk, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы k.(Приложение № 3 методички, или в любой книге по статистике.)Если trtk, то величина коэффициента корреляции признается существенной. Для оценки значимости индекса корреляции R применяется F-критерий Фишера. Фактическое значение критерия FR определяется по формуле  (16)где m – число параметров уравнения регрессии. Величина FR сравнивается с критическим значением Fk, которое определяется по таблице F-критерия с учетом принятого уровня значимости и числа степеней свободы v1 = m – 1 и v2 = n – m.Если FRFk, то величина индекса корреляции признается существенной. Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации  .Значение средней ошибки аппроксимации, определяемой по формуле:  (17)не должно превышать 12-15%. Для получения выводов с практической значимости синтезированных в анализе моделей показателям тесноты связи дается качественная оценка. Это осуществляется на основе шкалы Чеддока (табл. 1). Таблица 1 Шкала Чеддока
Заметим, что функциональная связь обозначается 1, а отсутствие связи – 0. При обозначениях показателей тесноты связи, превышающих 0,7, зависимость результативного признака y от факторного x является высокой, а при значении более 0,9 – весьма высокой. Это в соответствии с показаниями индекса детерминации R2 означает, что более половины общей вариации результативного признака y объясняется влиянием изучаемого фактора x. Последнее позволяет считать оправданным применением метода функционального анализа для получения корреляционной связи, а синтезированные при этом математические модели признаются пригодными для их практического использования. При показаниях тесноты связи ниже 0,7 величина индекса детерминации R2 всегда будет меньше 50%. Это означает, что на долю вариации факторного признака Х приходится меньшая часть по сравнению с прочими признаками, влияющими на изменение общей дисперсии результативного признака. Синтезированные при таких условиях модели связи практического значения не имеют. При анализе адекватности уравнения регрессии исследуемому процессу возможны следующие варианты.
С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности, определяемые по формуле:  , где  - среднее значение соответствующего факторного признака; - среднее значение результативного признака;ai - коэффициент регрессии при соответствующем факторном признаке. Коэффициент эластичности показывает на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%. Рассмотрим применение методов корреляционно-регрессионного анализа влияния вариации факторного показателя x на результативный yна конкретных примерах. Пример 1. Используя данные таблицы 2, выявите характер связи между факторными и результативными признаками. Изобразите корреляционную связь графически. Измерьте тесноту связи с помощью коэффициента корреляции. Постройте адекватное уравнение регрессии, рассчитайте коэффициент Фишера и ошибку аппроксимации. Сделайте выводы Таблица 2 |
, отображающая общее влияние всех факторов
, отражающая вариацию y только от воздействия изучаемого фактора x
, отражающая вариацию результативного признака y от всех прочих, кроме x, факторов