Статистика - лекция - Корреляция. Статистическое изучение взаимосвязи социальноэкономических явлений. Корреляционнорегрессионный анализ
 Скачать 0.86 Mb.
|
Производство и себестоимость продукции на одном из заводовТамбовской области в 2011 году
По данным о себестоимости единицы продукции и объёма произведенной продукции определим направление и тесноту связи между признаками. Представим вышеприведенные данные в таблице 5 после предварительной их обработки методом приведения параллельных данных. Сопоставив полученные ряды данных x и y можно наблюдать наличие обратной зависимости между признаками, когда увеличение объёма произведенной продукции ведёт к снижению себестоимости единицы продукции. Исходя из этого, можно сделать предположение, что связь между признаками обратная, и ее можно описать уравнением гиперболы. Этот же вывод подтверждается и на основе графического анализа (рис.2). Анализ рис.2 показывает наличие близкой к криволинейной зависимости, так как точки расположены по кривой линии – допустим, что это гипербола. Уравнение гиперболы: 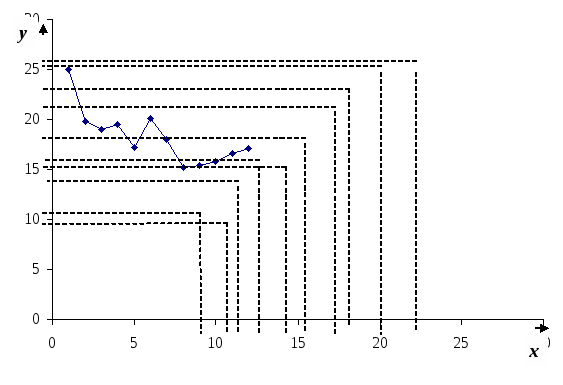  Рис. 2. Зависимость себестоимости единицы продукции от объёма произведенной продукции. Определим параметры уравнения гиперболы на основе метода наименьших квадратов. Исходные данные и расчетные показатели представлены в таблице 5. Систему нормальных уравнений для нахождения параметров гиперболы можно представить следующим образом:     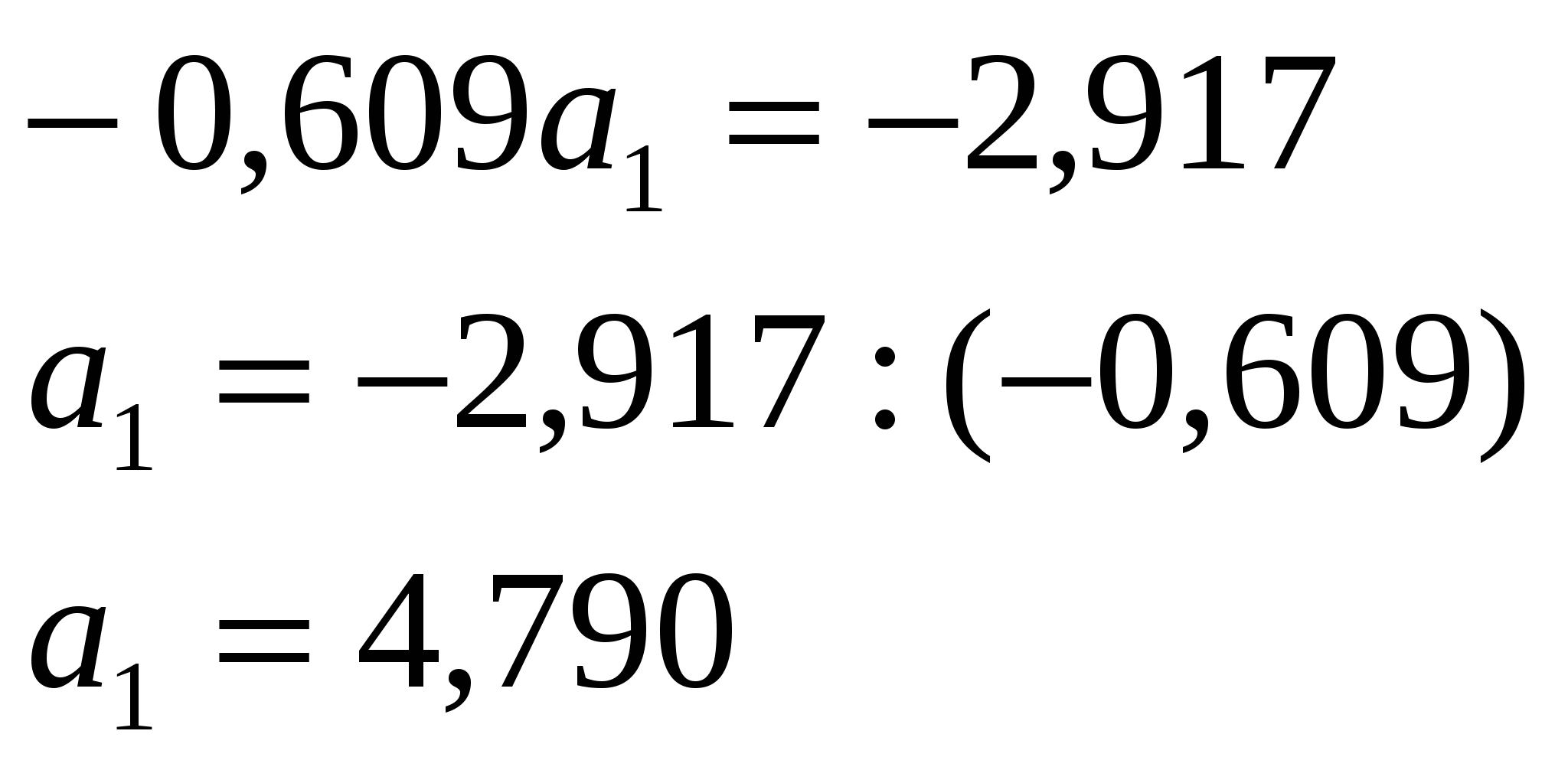  –  Из первого уравнения вычитаем второе. Далее 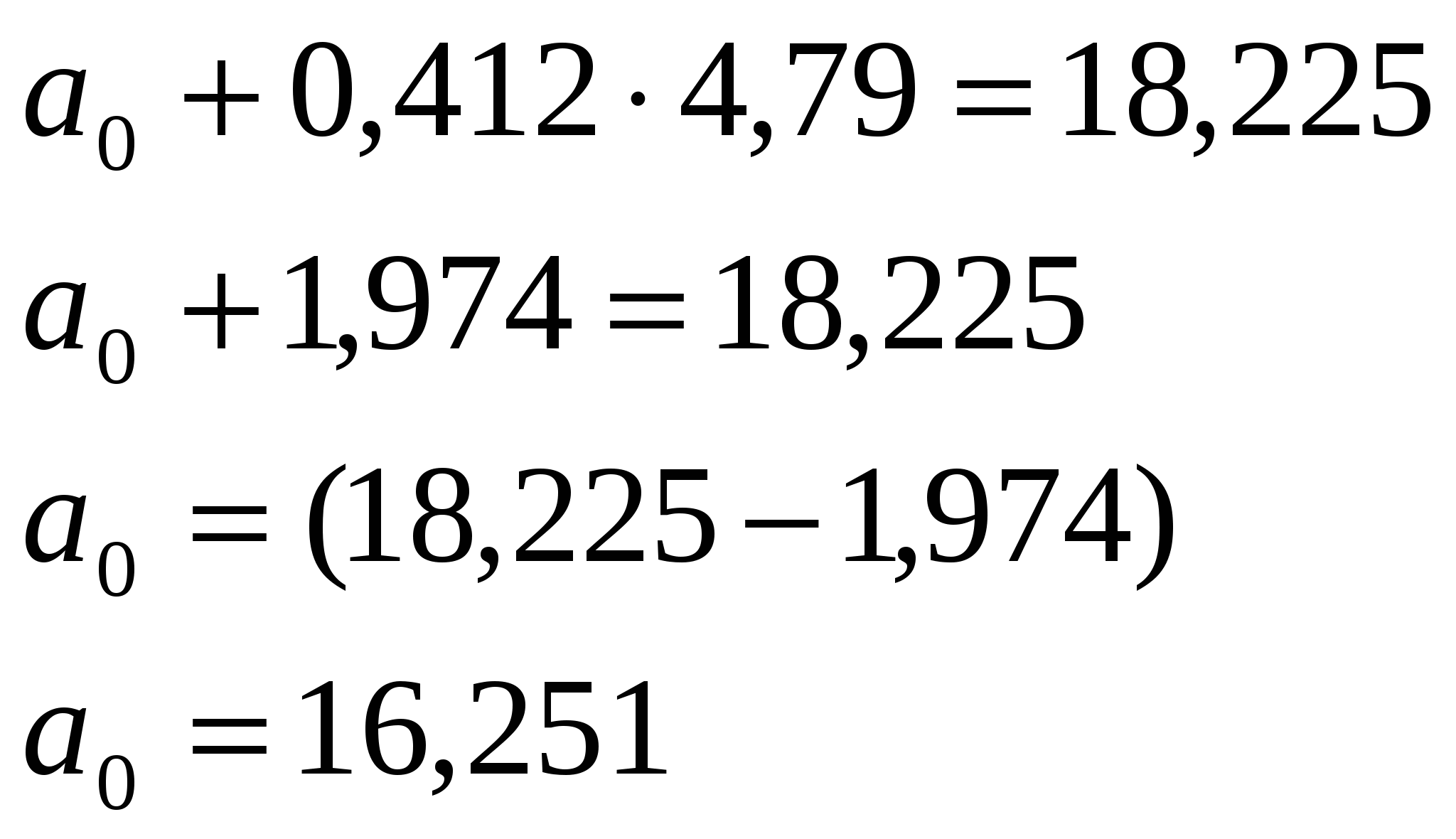 Уравнение гиперболы:  Отсюда:  (19)В уравнении регрессии а1 = 4,79 – коэффициент регрессии показывает, что с увеличением производства продукции на 1 тыс. штук, себестоимость продукции сокращается на 4,79 руб. Проверим параметры данного уравнения на типичность. Для этого, используя формулы (3), (4), (5), (6), рассчитаем необходимые данные. 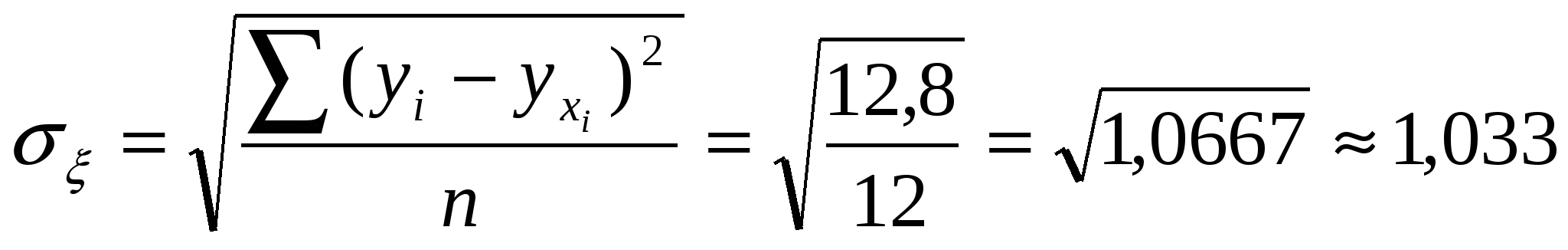     На основании выявленной модели (19) определим теоретические (выровненные значения себестоимости в зависимости от количества произведенной продукции) и запишем в табл. 5 (гр. 7):             Таблица 5 |