Расчётная таблица
№п/п
|
Произведено продукции, тыс. штук, Х
|
Себестоимость
единицы продукции, руб. У
|
Ранги
|
Разность
рангов
di = Rх - Rу
|
di2
|
Rх
|
Rу
|
1.
|
0,5
|
25,0
|
1
|
12
|
-11
|
121
|
2.
|
1,8
|
20,1
|
2
|
11
|
-9
|
81
|
3.
|
2,0
|
19,8
|
3
|
10
|
-7
|
49
|
4.
|
2,5
|
19,5
|
4
|
9
|
-5
|
25
|
5.
|
3,1
|
19,0
|
5
|
8
|
-3
|
9
|
6.
|
3,4
|
18,0
|
6
|
7
|
-1
|
1
|
7.
|
5,4
|
16,6
|
7
|
4
|
3
|
9
|
8.
|
5,8
|
17,2
|
8
|
6
|
2
|
4
|
9.
|
6,0
|
15,8
|
9
|
3
|
6
|
36
|
10.
|
7,2
|
17,1
|
10
|
5
|
5
|
25
|
11.
|
8,3
|
15,4
|
11
|
2
|
9
|
81
|
12.
|
12,0
|
15,2
|
12
|
1
|
11
|
121
|
Итого
|
|
|
|
|
|
562
|
ρ 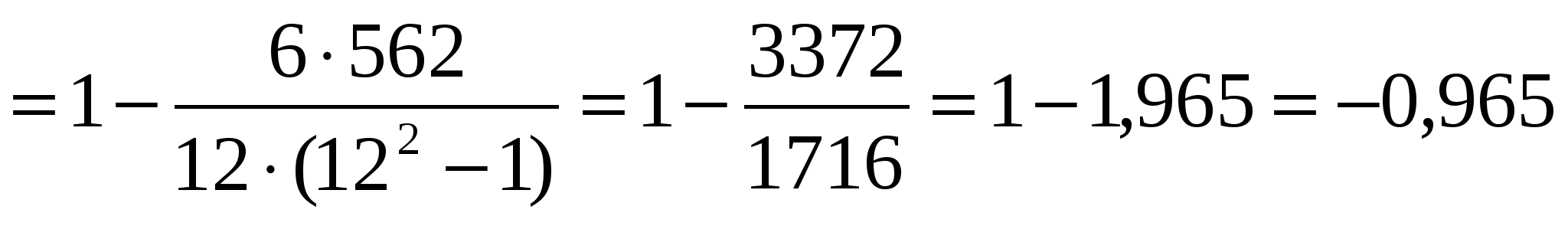
Пользуясь определением тесноты связи по шкале Чеддока, можно сказать, что полученная связь очень сильная, обратная.
Коэффициент Спирмена принимает любые значения в интервале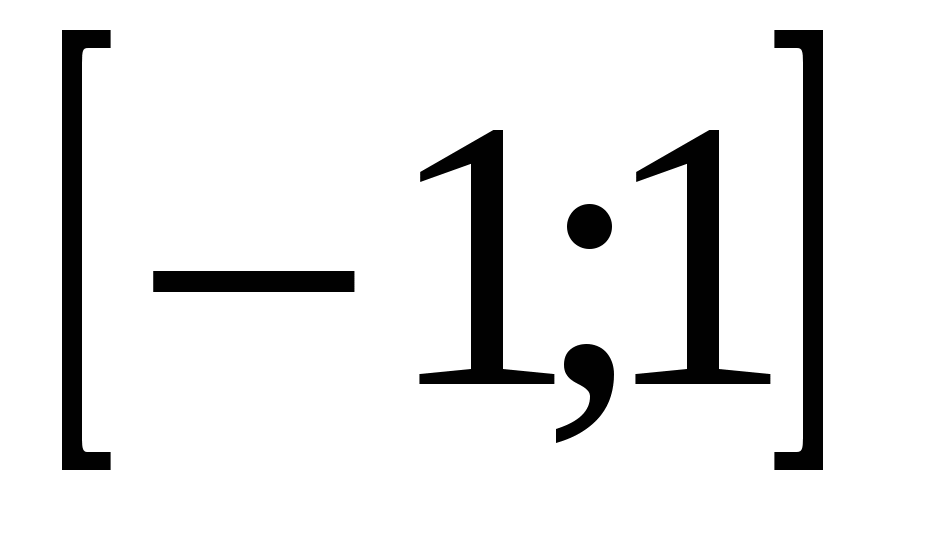 . Значимость коэффициента корреляции рангов Спирмена проверяется на основе t – критерия Стьюдента по формуле: . Значимость коэффициента корреляции рангов Спирмена проверяется на основе t – критерия Стьюдента по формуле:
tp = ρх/у 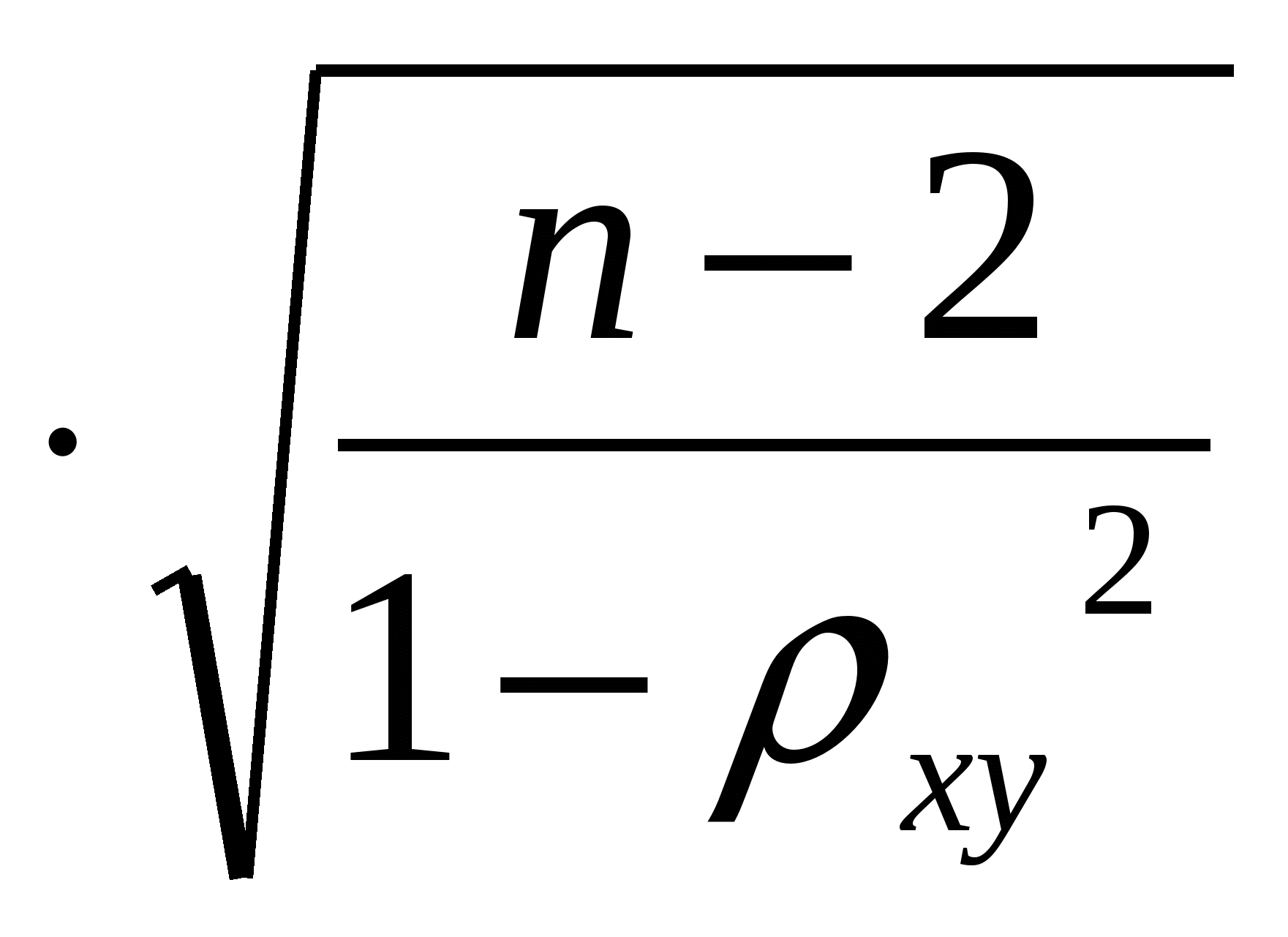 ; tp = - 0,965 ; tp = - 0,965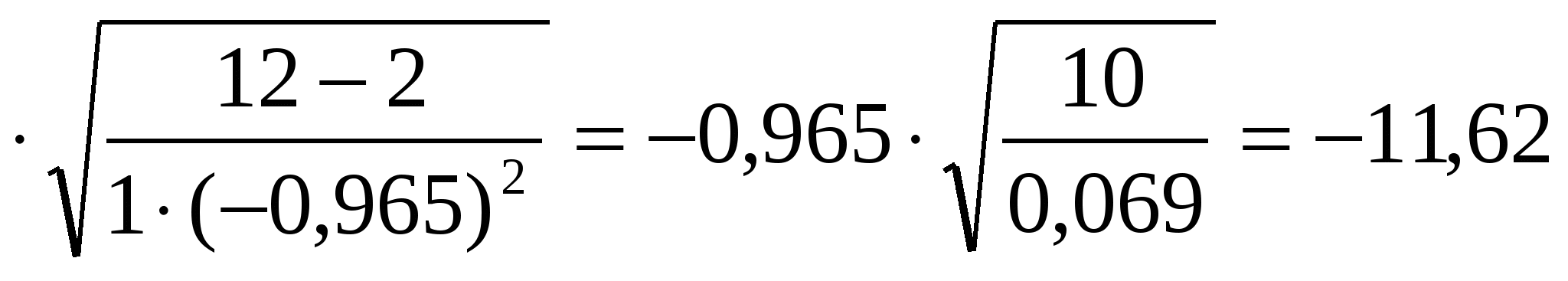
Значение коэффициента корреляции считается статистически существенным, если tp tk . При tk . При 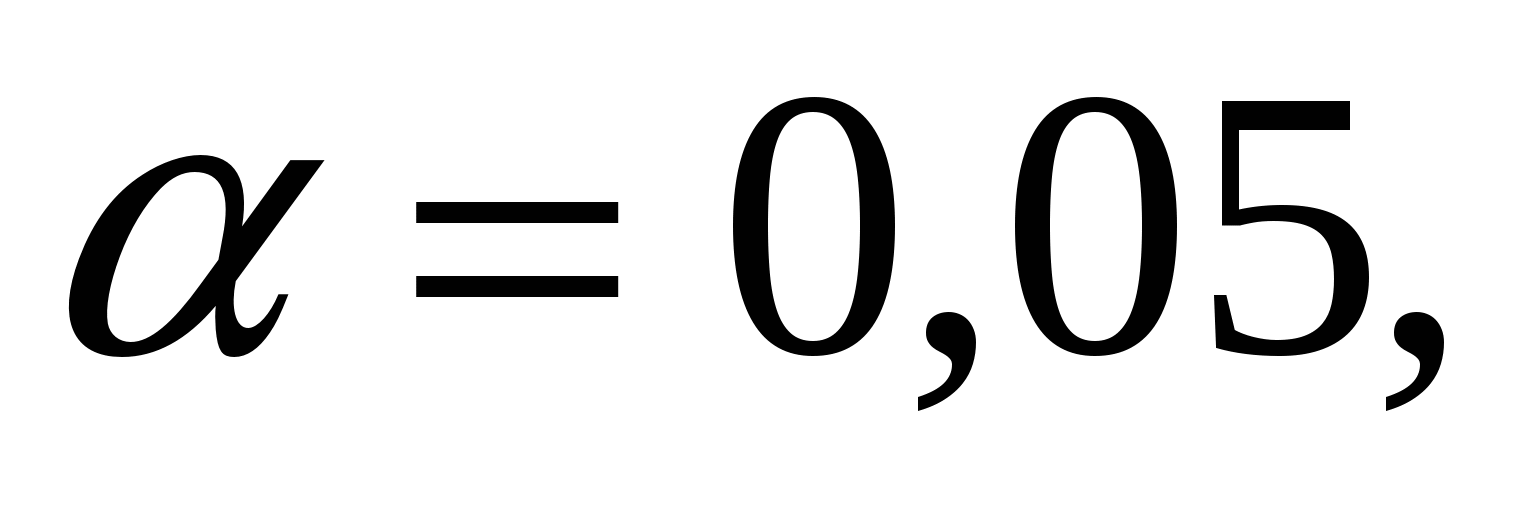 k = n - 2 tk=2,228 11,62 k = n - 2 tk=2,228 11,62 2,228 2,228
Ранговый коэффициент Кендалла ( ) используется для измерения взаимосвязи между количественными и качественными признаками, характеризующими однородные объекты, ранжированные по одному принципу. Расчёт коэффициента Кендалла осуществляется по формуле: ) используется для измерения взаимосвязи между количественными и качественными признаками, характеризующими однородные объекты, ранжированные по одному принципу. Расчёт коэффициента Кендалла осуществляется по формуле:
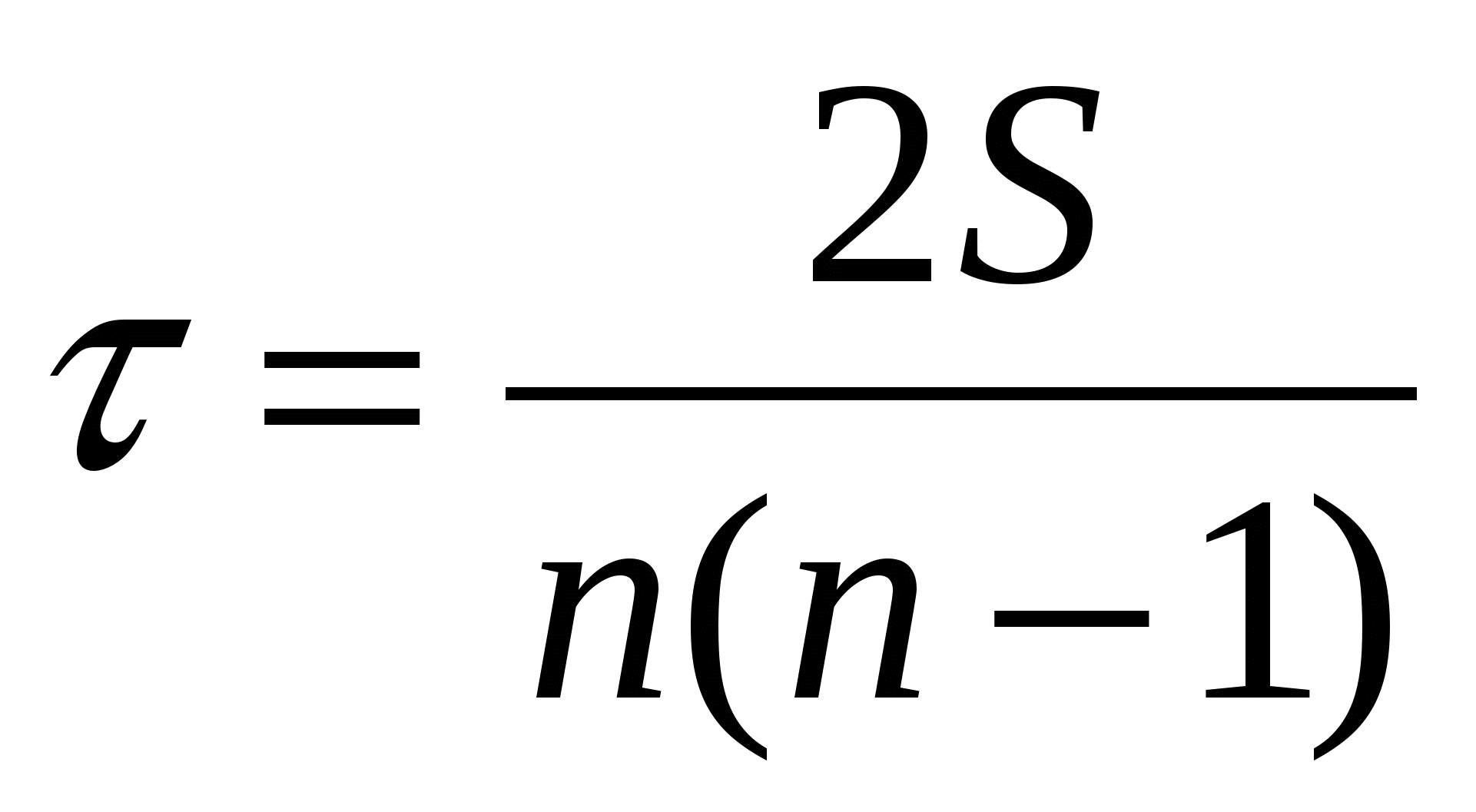 , ,
где S = P + Q , n – число наблюдений, S – сумма разностей между числом последовательностей и числом инверсий по второму признаку.
Расчёт данного коэффициента выполняется в следующей последовательности:
значения Х ранжируются в порядке возрастания или убывания
значения У ранжируются в порядке, соответствующем значениям Х.
для каждого ранга У определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяют величину Р как меру соответствия последовательности рангов по Х и У. Она учитывается со знаком +.
для каждого ранга У определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком - .
определяется сумма баллов по всем членам ряда.
Пример 3: В качестве примера возьмём данные предыдущего примера и заполним таблицу 13.
Таблица 13
Расчётная таблица
Ранг продукции по производству Х
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
Ранг по себестоимости У
|
12
|
11
|
10
|
9
|
8
|
7
|
4
|
6
|
3
|
5
|
2
|
1
|
Р = 0 + 0 + 0 + 0 + 0 +0
Q = -11 – 10 - 9 - 8 - 7 - 6 - 3 – 4 - 2 - 2 - 2 -1 = -63
S = 0 + (-63) = -63
 = = 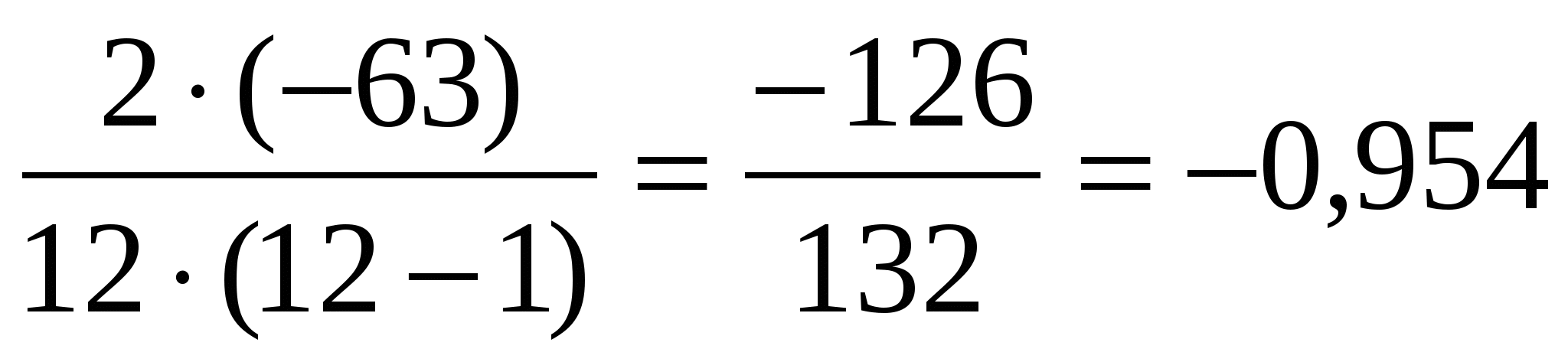 . Связь между признаками можно признать значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла >0,5. . Связь между признаками можно признать значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла >0,5.
Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) W, который вычисляется по формуле:
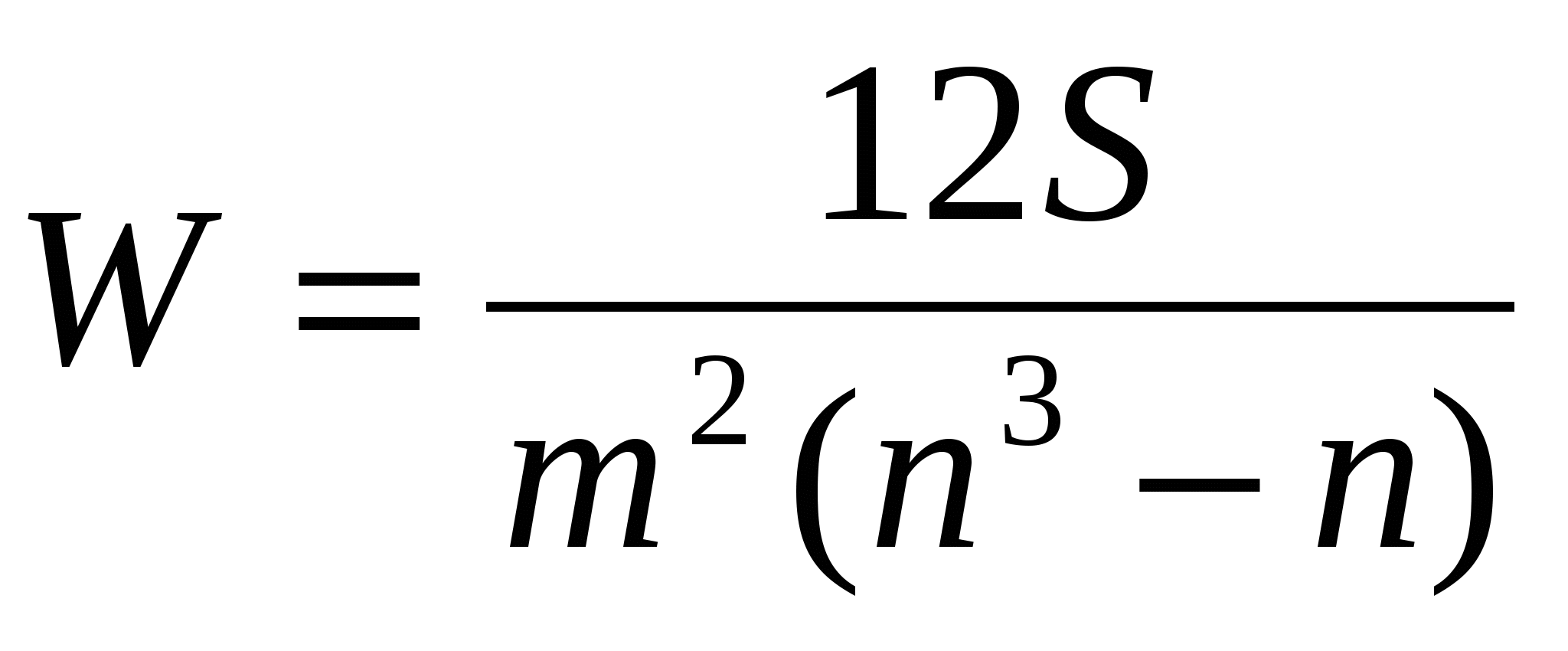 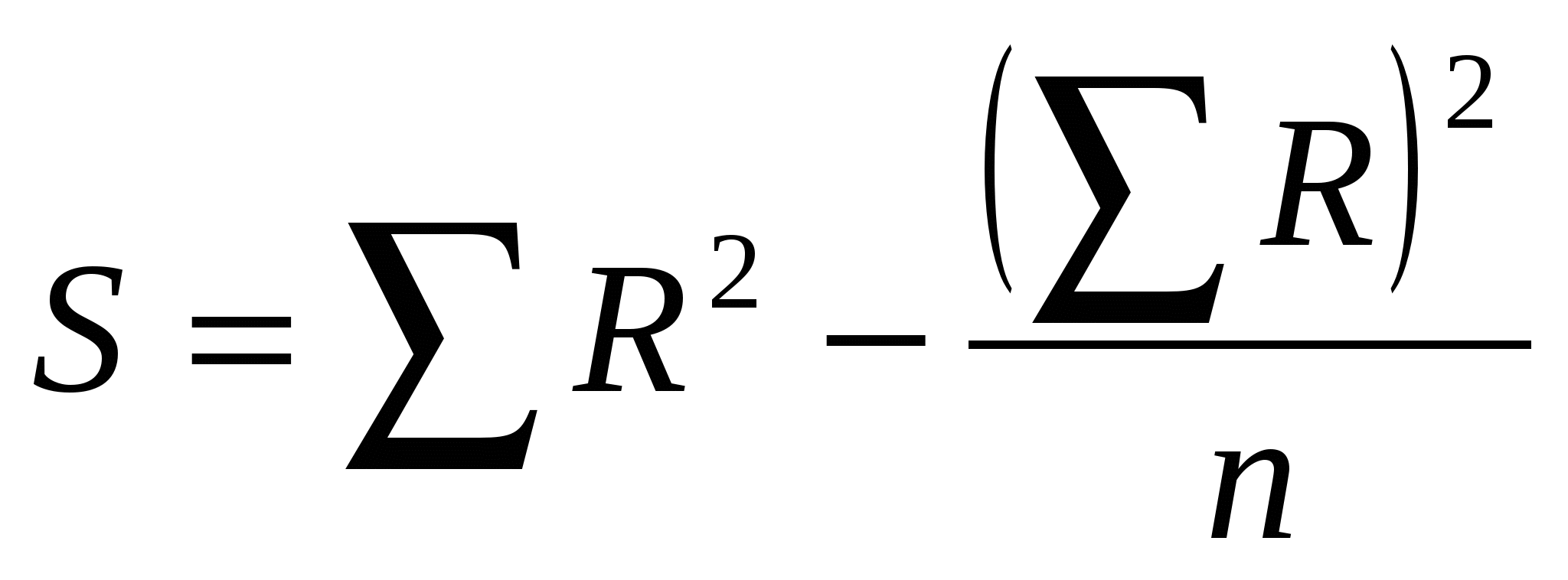
где m – количество факторов n – число наблюдений
S – отклонение суммы квадратов рангов от средней квадратов рангов.
Пример 4: по данным таблицы 14 о фондовооружённости и фондообеспеченности определить зависимость между ними и производительностью труда.
Таблица 14
Расчетная таблица
Фондовооруженность X1
|
Фондообеспеченность X2
|
Производительность Y
|
Rx1
|
Rx2
|
Ry
|
Сумма строк рангов
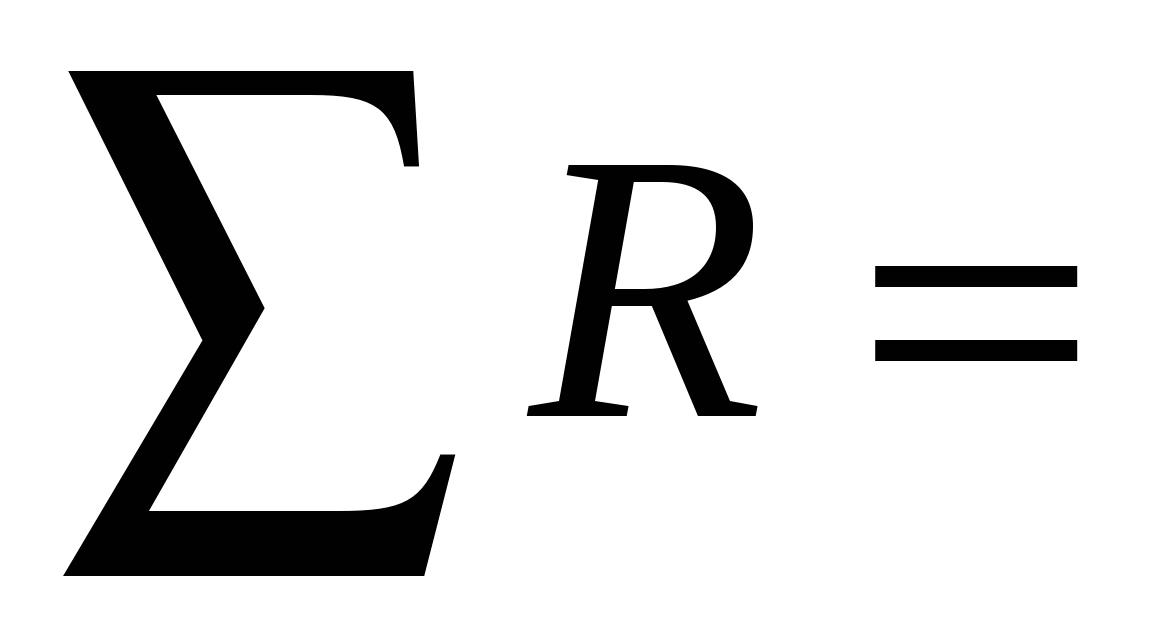 Rx1+ Rx2 Rx1+ Rx2
|
Квадраты рангов
R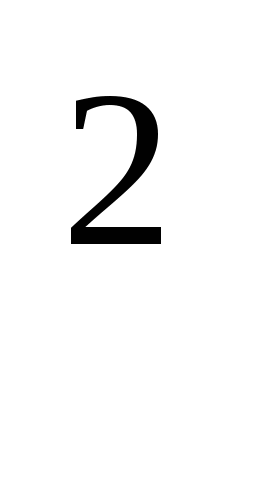
|
9,6
11,3
11,9
13,3
14,8
16,0
17,8
18,7
20,7
22,8
|
65,4
71,0
76,0
88,9
94,4
100,5
102,9
106,7
112,4
121,8
|
4,8
4,4
5,9
6,7
6,5
7,6
8,8
9,6
10,5
10,6
|
1
2
3
4
5
6
7
8
9
10
|
1
2
3
4
5
6
7
8
9
10
|
2
1
3
5
4
6
7
8
9
10
|
4
5
9
13
14
18
21
24
27
30
|
16
25
81
169
196
324
441
576
729
900
|
|
|
|
|
|
|
165
|
3457
|
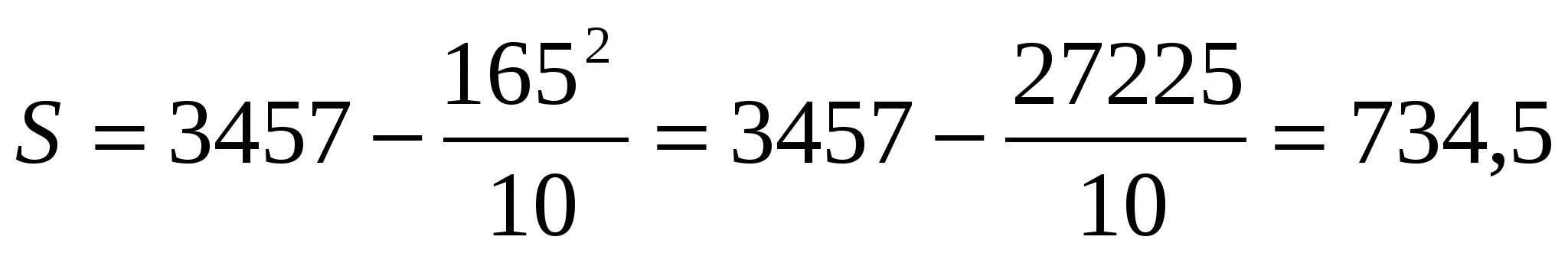
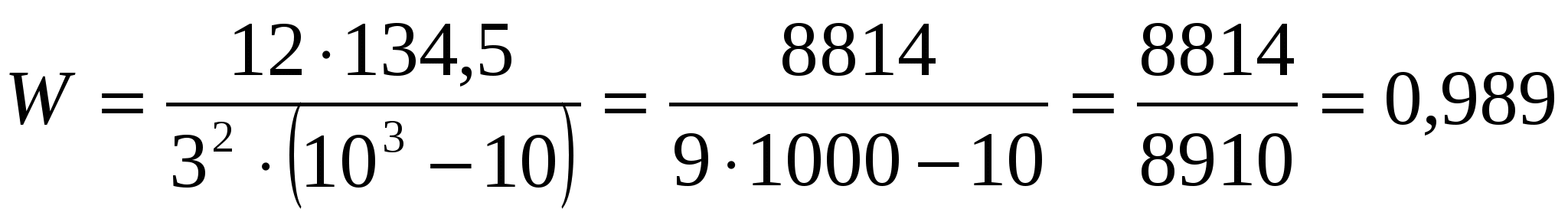
Связь тесная.
Значимость коэффициента конкордации проверяется на основе x2- критерия Пирсона:
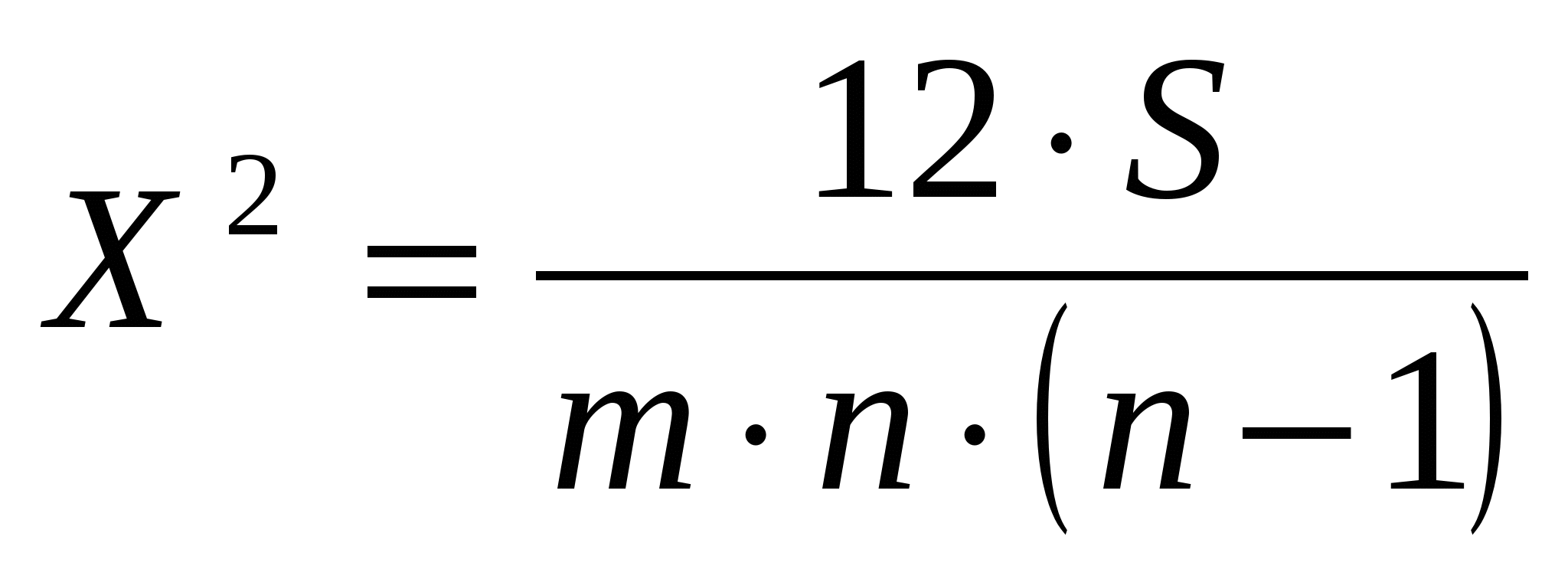
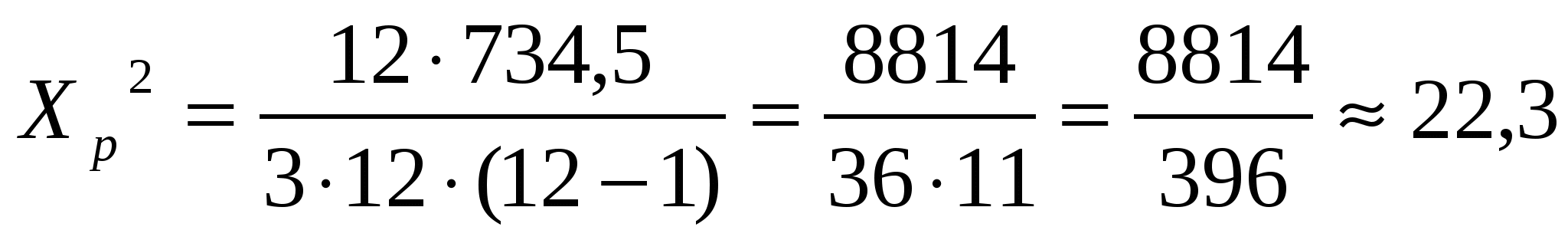
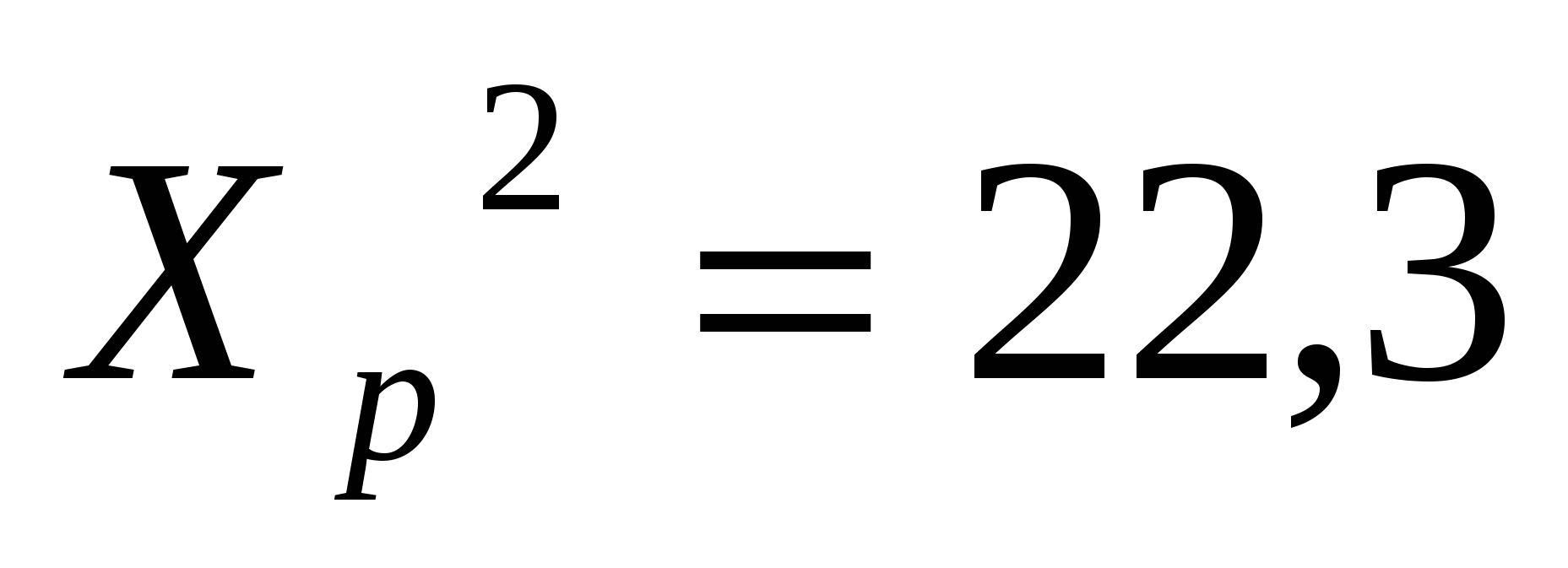 > >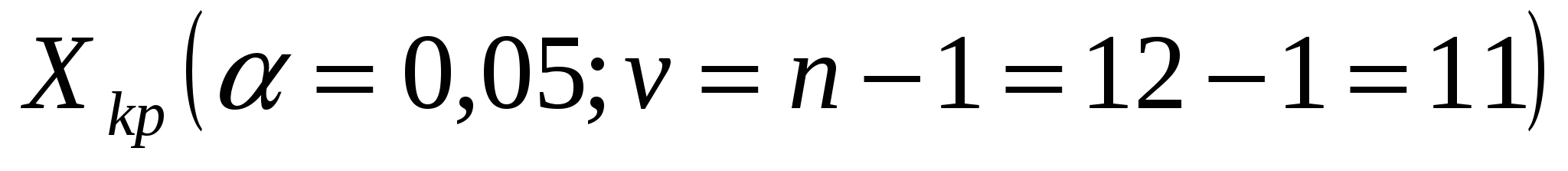 22,3>2,201 22,3>2,201
Ранговые коэффициенты корреляции Спирмена, Кендалла и конкордации имеют преимущество, что с помощью их можно измерить и оценить связи как между количественными, так и между атрибутивными признаками, которые поддаются ранжированию.
Контрольные вопросы:
1. Сформулируйте определение корреляционной зависимости.
Дайте классификацию статистических связей по направлению.
С помощью какого коэффициента корреляции оценивается связь между двумя признаками?
Какие показатели используются в оценке связей качественных признаков?
Для каких признаков используются ранговые коэффициенты корреляции?
Дайте экономическую интерпретацию коэффициента регрессии а1.
В каких пределах изменяются коэффициенты конкордации?
|
 Скачать 0.86 Mb.
Скачать 0.86 Mb.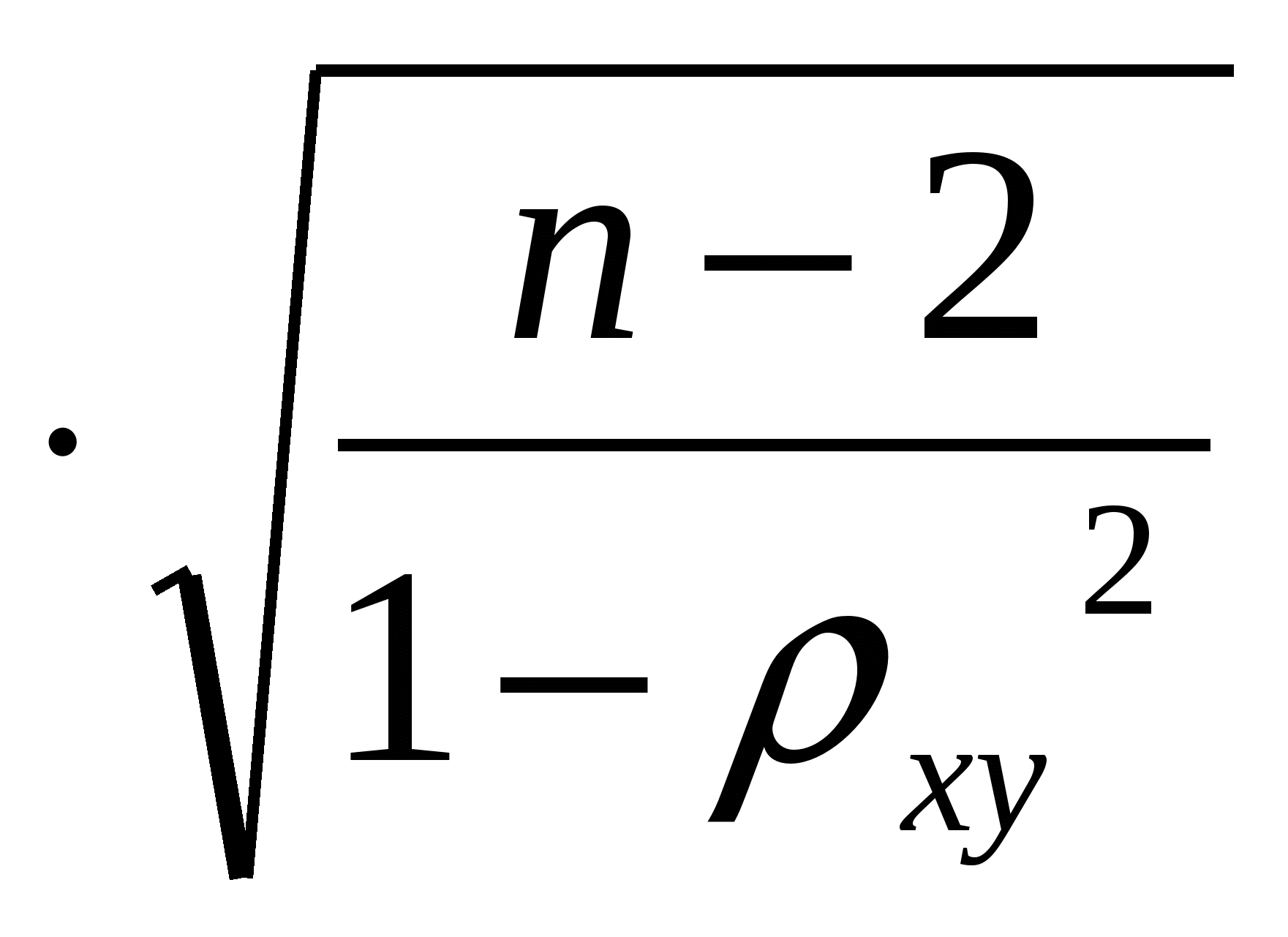 ; tp = - 0,965
; tp = - 0,965