Статистика - лекция - Корреляция. Статистическое изучение взаимосвязи социальноэкономических явлений. Корреляционнорегрессионный анализ
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
Из второго уравнения вычтем первое, а из третьего – второе, получим: -8,6441а2=1,9477 а2 = - 0,2253 Величину параметра а1 определим из следующего уравнения: 0,2496а1 + 0,2839 ·(- 0,2253) = - 1,0155 0,2496а1 - 0,0640 = - 1,0155 0,2496а1 = -1,0155 + 0,0640 а1 = - 0,9515: 0,2496 а1 = - 3,8121 Величину параметра а0 определим из следующего уравнения: а0 + 5,4341 · (- 3,8121) + 23,275 · (- 0,2253) = - 6,5224 а0 - 20,7153 – 5,2439 = - 6,5224 а0 = - 6,5224 + 20,7153 + 5,2439 а0 = 19,4368 Таким образом, получаем уравнение, выражающее корреляционную зависимость между численностью безработных, численностью занятых в условиях, не отвечающих санитарным нормам, и естественным приростом (убылью) населения в расчёте на 1000 жителей в анализируемых областях: Ух1х2 = 19,4368 - 3,8121х1 – 0,2253х2 В данном уравнении регрессии параметр а0 = 19,4368 показывает усреднённое влияние на результативный признак неучтённых (невыделенных для исследования) факторов; параметр а1 = - 3,8121 – коэффициент регрессии, который показывает, что с увеличением численности безработных на 1% - естественный прирост (убыль) населения в расчёте на 1000 жителей уменьшается на 3,8 человека; параметр а2 = - 0,2253 – коэффициент регрессии, который показывает, что с увеличением численности занятых в условиях, не отвечающих санитарным нормам, на 1% - естественный прирост (убыль) населения в расчёте на 1000 жителей уменьшается на 0,2 человека. г) Вычислим коэффициенты парной корреляции  , где , где   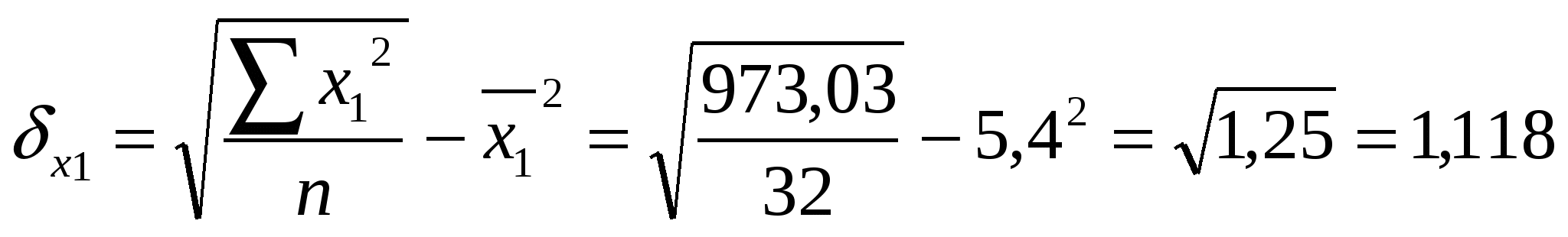 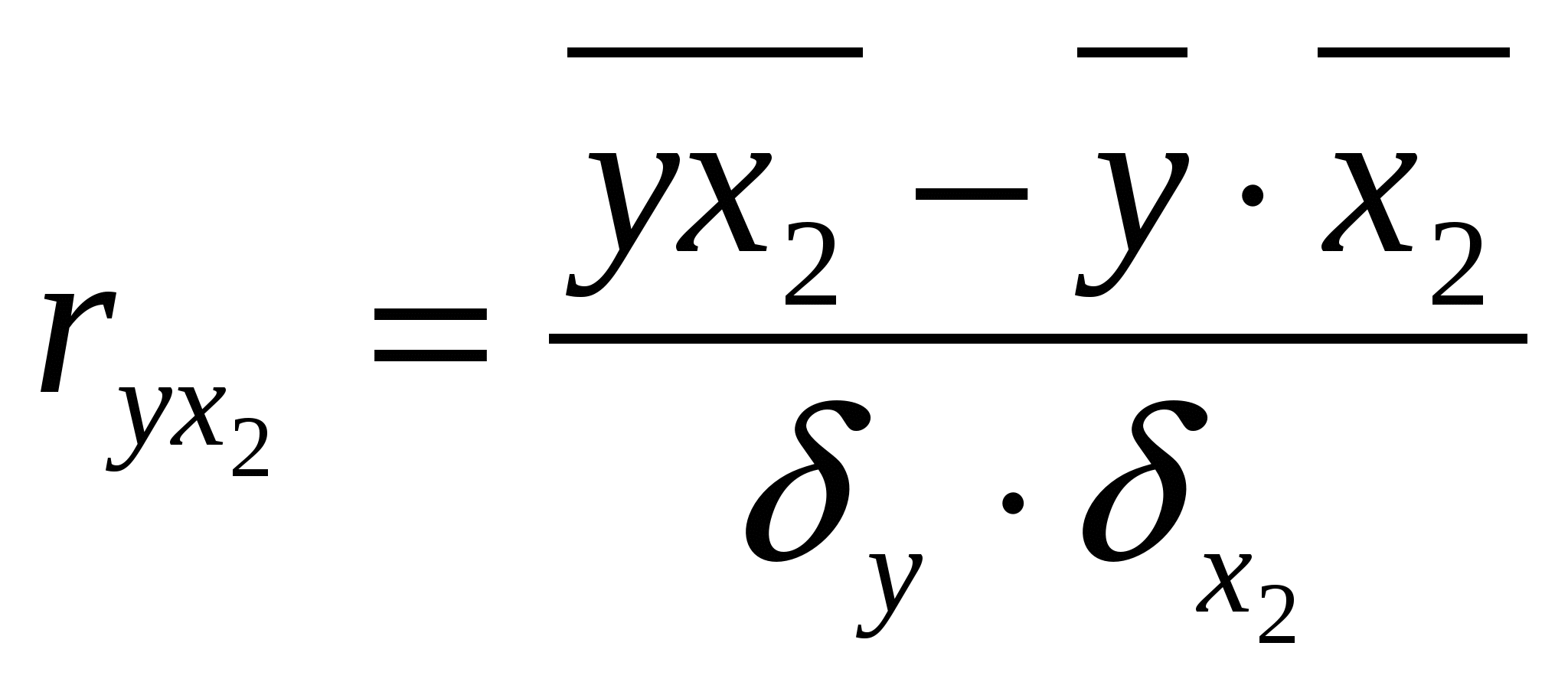 , где , где 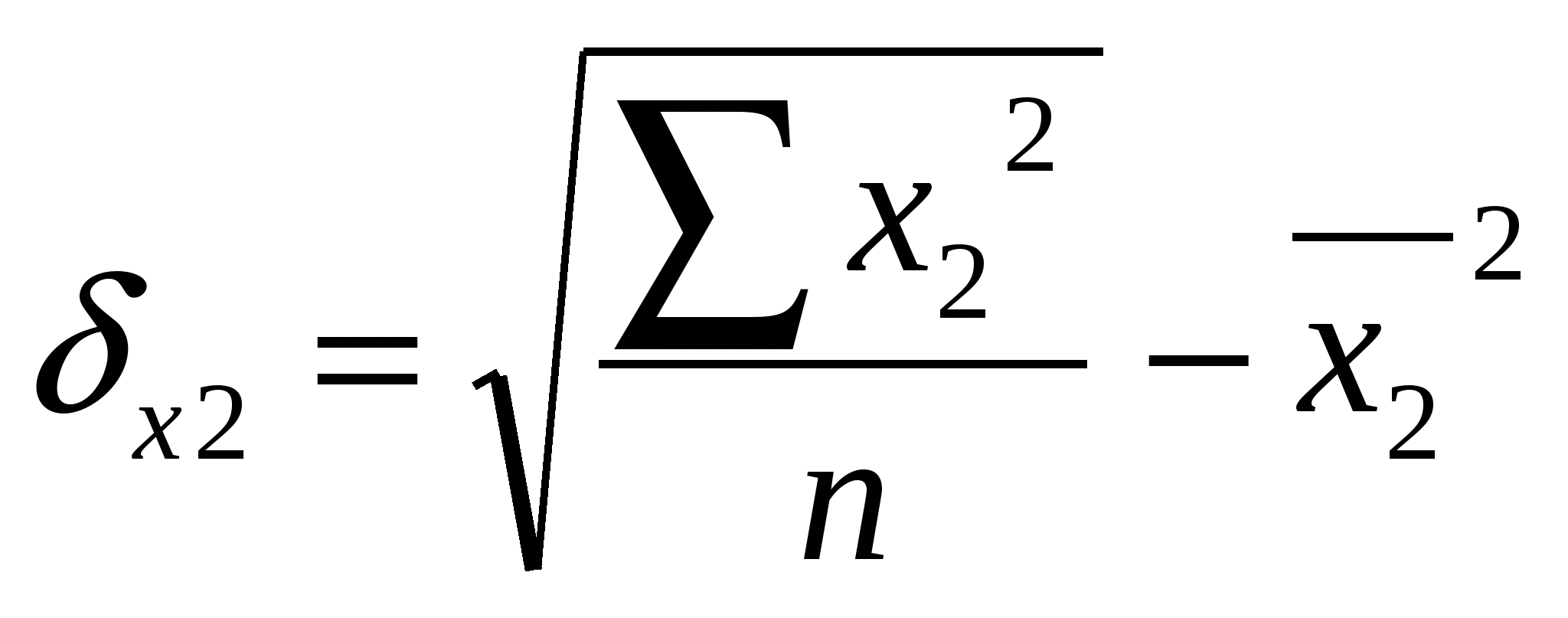 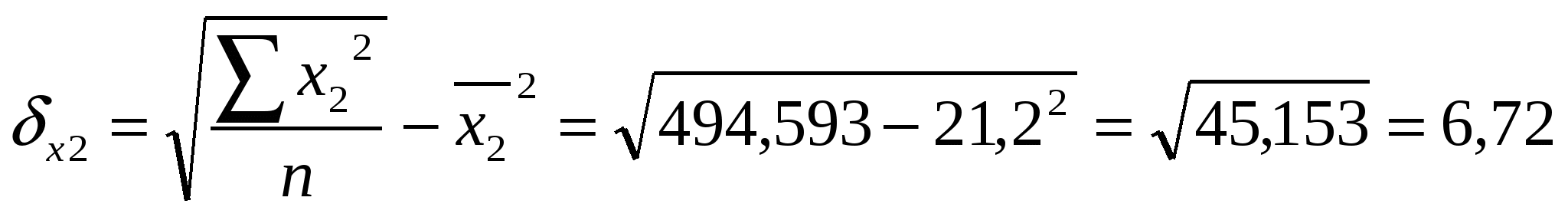 Вычисленные коэффициенты парной корреляции показывают тесноту связи между численностью безработных, численностью занятых в условиях, не отвечающих санитарным нормам, и естественным приростом (убылью) населения в расчёте на 1000 жителей в анализируемых областях. Так, д) Множественный коэффициент корреляции для двух факторных (Х1 и Х2) признаков вычисляется по формуле:  , где , гдеrух - парные коэффициенты корреляции между признаками. Следовательно, в нашей задаче, множественный коэффициент корреляции равен: 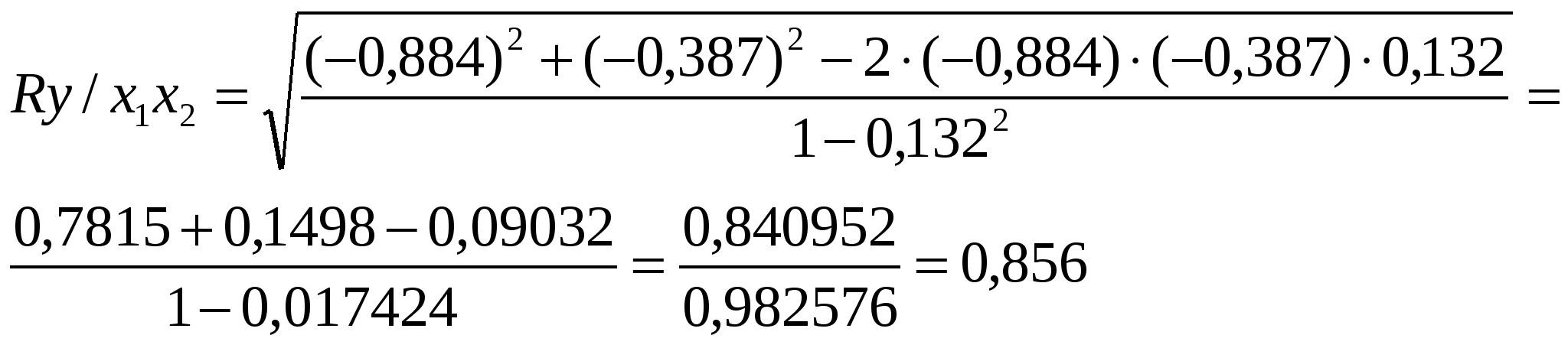 Коэффициент множественной корреляции изменяется в пределах от 0 до 1 и по определению положителен: 0 ≤ R≤1. Приближение Rк единице свидетельствует о сильной зависимости между признаками. Следовательно, вычисленный коэффициент множественной корреляции  е) Вычислим частные коэффициенты корреляции, которые характеризуют степень тесноты связи между двумя признаками х1 и х2 при фиксированном значении других (k - 2) факторных признаков, то есть когда влияние х1 исключается, то есть оценивается связь между х1 и х2 в "чистом виде". В случае зависимости у от двух факторных признаков х1 и х2 коэффициенты частной корреляции имеют вид:  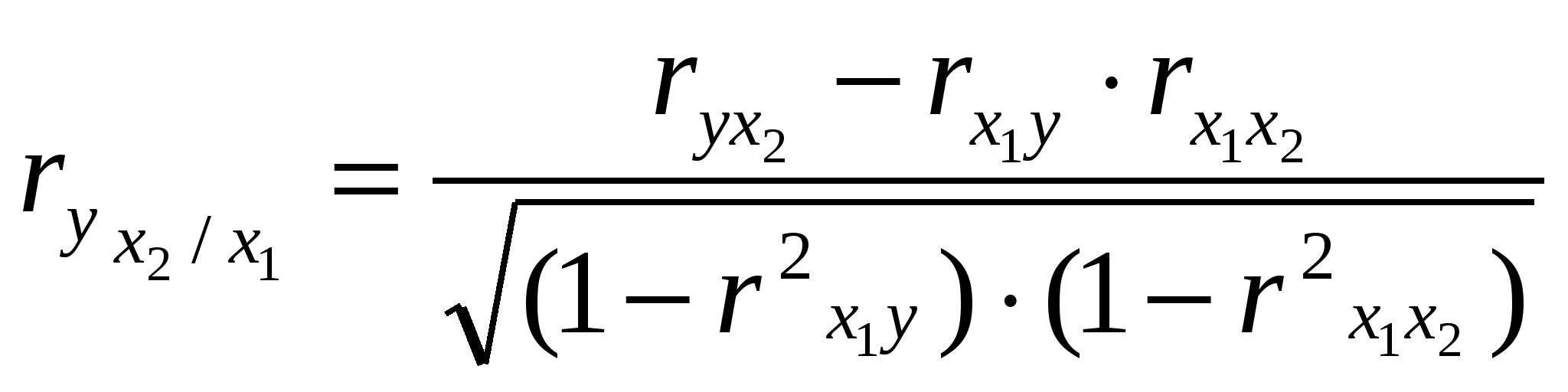 , , где r – парные коэффициенты корреляции между указанными в индексе переменными. В первом случае исключено влияние факторного признака х2, во втором – х1. В нашей задаче: 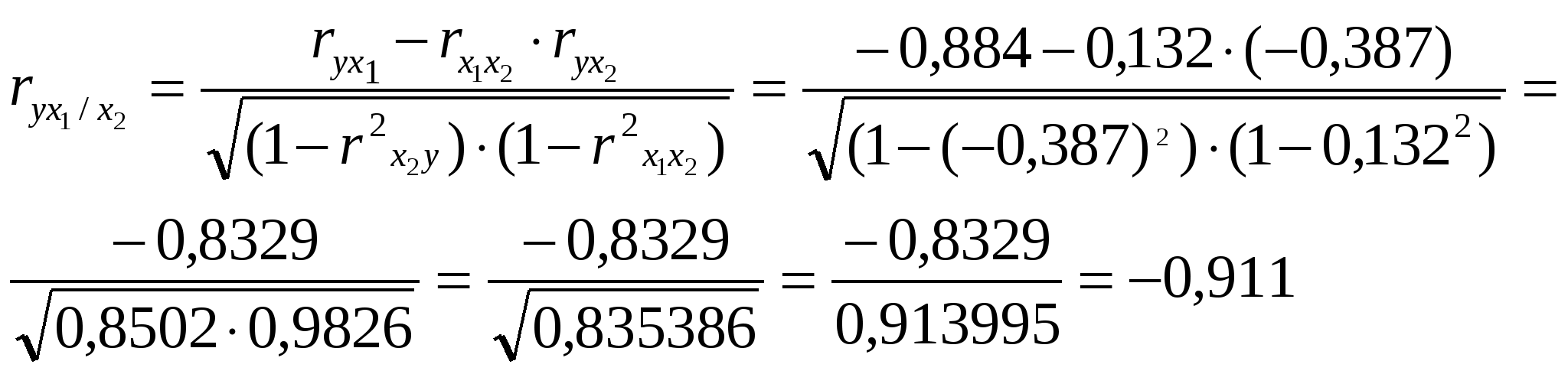 Значит, между численностью безработных (Х1) и естественным приростом (убылью) населения в расчёте на 1000 жителей (У) при фиксированном значении показателя Х2 наблюдается высокая (по шкале Чеддока), обратная (т. к. знак «-») зависимость. 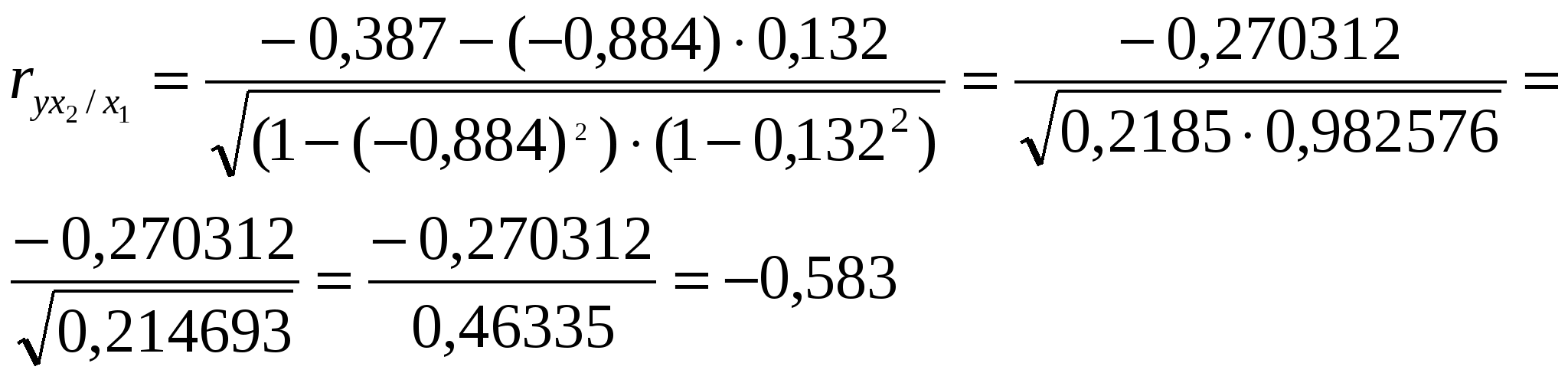 Следовательно, между численностью занятых в условиях, не отвечающих санитарным нормам (Х2), и естественным приростом (убылью) населения в расчёте на 1000 жителей (У) при фиксированном значении показателя Х1 наблюдается заметная (по шкале Чеддока), обратная (т. к. знак «-») зависимость. 5. Непараметрические методы анализа. Как мы изучили на предыдущих занятиях, для изучения тесноты связи между Х и У используется коэффициент (индекс) корреляции. В некоторых случаях мы можем встретиться с такими качествами, которые не поддаются выражению числом единиц. Эти обстоятельства заставляют прибегать к использованию т. н. непараметрических методов, позволяющих измерить интенсивность связи как между количественными признаками, так и между качественными. При исследовании тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации (Ка) и контингенции (Кк) . Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т. е. состоящим из двух качественно отличных друг от друга значений признака (табл. 8). Таблица 8 Таблица для вычисления коэффициентов ассоциации и контингенции
Коэффициенты вычисляются по формулам: ассоциации: контингенции: Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если Ка > 0,5 или Кк>0,3. Пример 1: Оцените наличие связи между студентами группы, распределённых по полу, и заинтересованностью их предметом «Статистика» (табл. 9), рассчитав Ка и Кк. (Данные получаем на основании опроса, проведенного в классе.) Таблица 9
Ка = Вывод: Т. к. Ка < 0,5 и Кк < 0,3 то заинтересованность статистикой не зависит от пола студентов. Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова, которые вычисляются по следующим формулам: 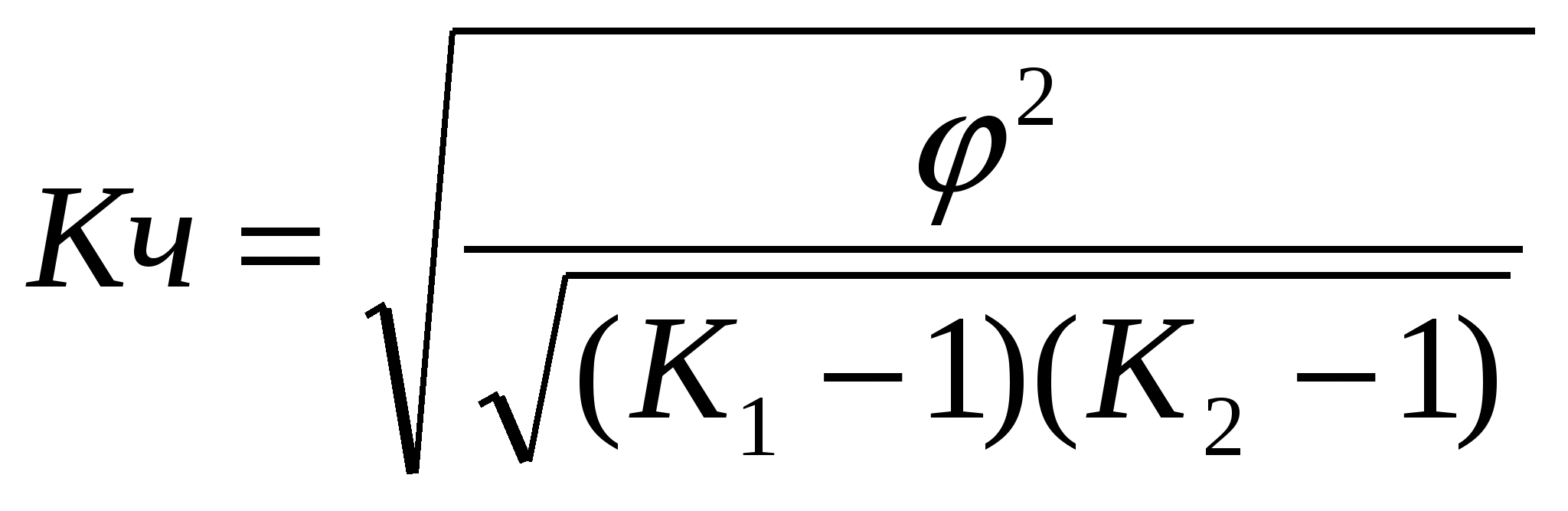 , , Где: 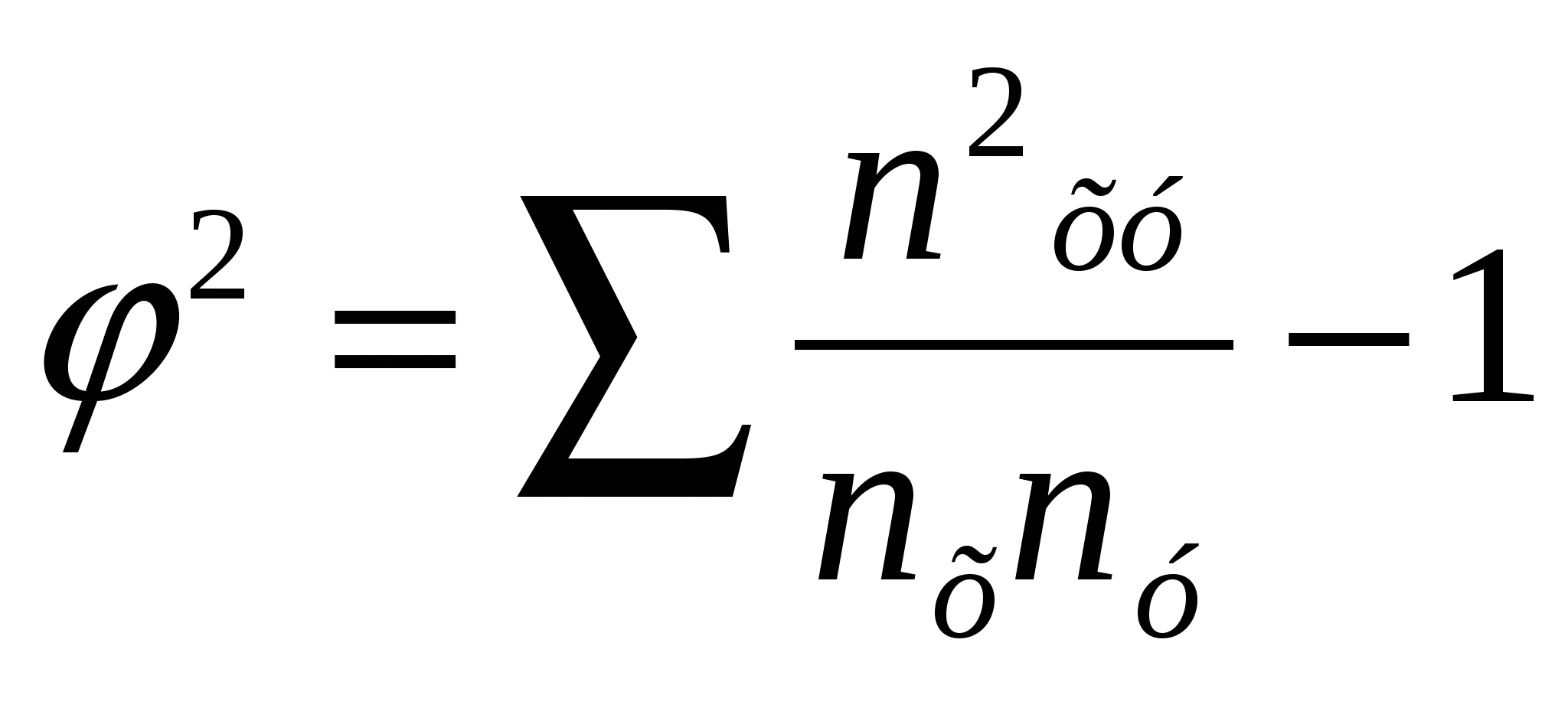 , , где К1- число значений (групп) первого признака К2- число значений (групп) второго признака Чем ближе Кп и Кч, тем связь теснее. Таблица 10 Вспомогательная таблица для расчёта коэффициента взаимной сопряжённости
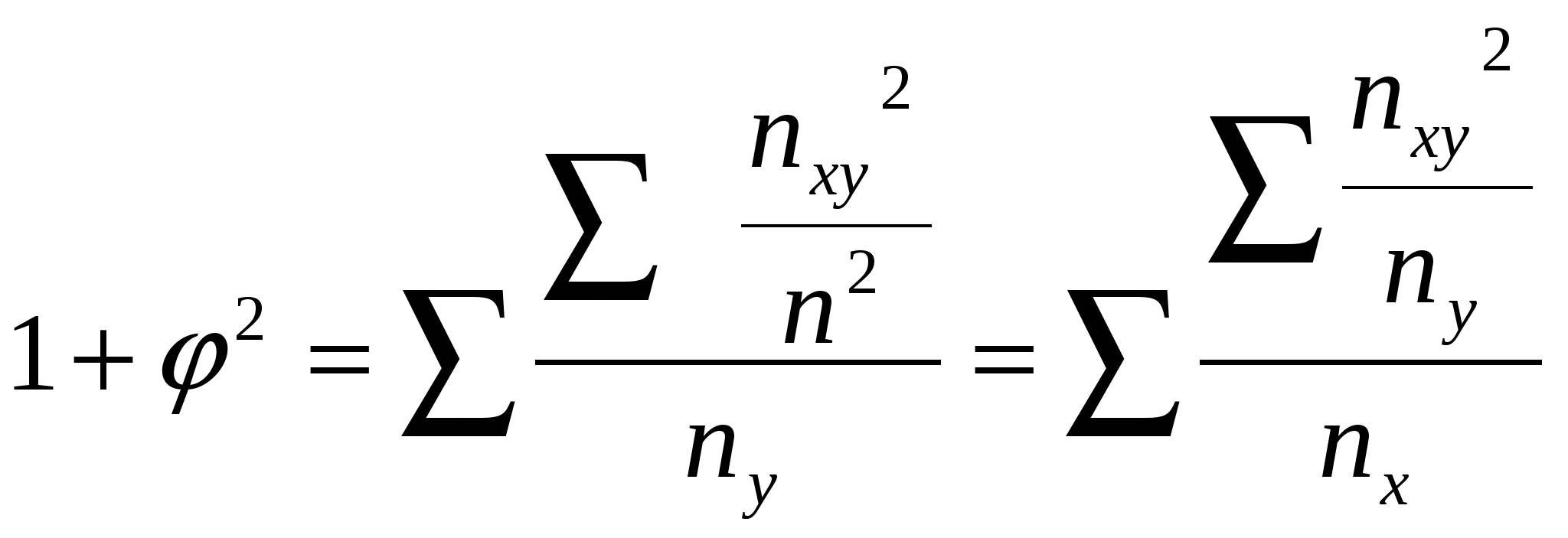 Пример 2. Оцените зависимость освоения курса «Статистика» от типа школы, которую окончили студенты данной группы (табл. 11) (исходные данные получаем путём опроса студентов группы непосредственно на занятии). Таблица 11 Зависимость освоения «Статистики» от типа школы, которую закончили студенты
Решение: Кп = 1 + 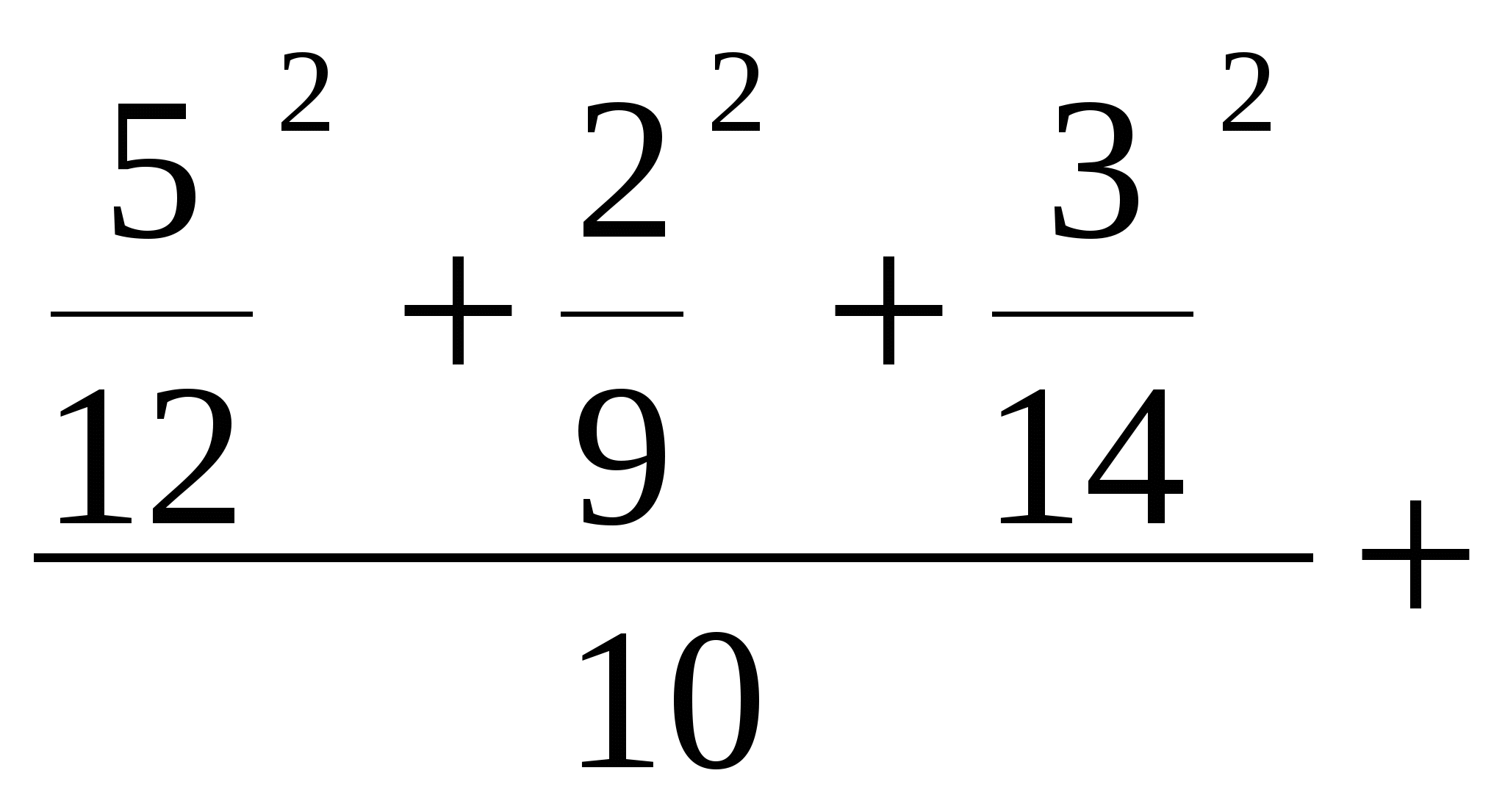 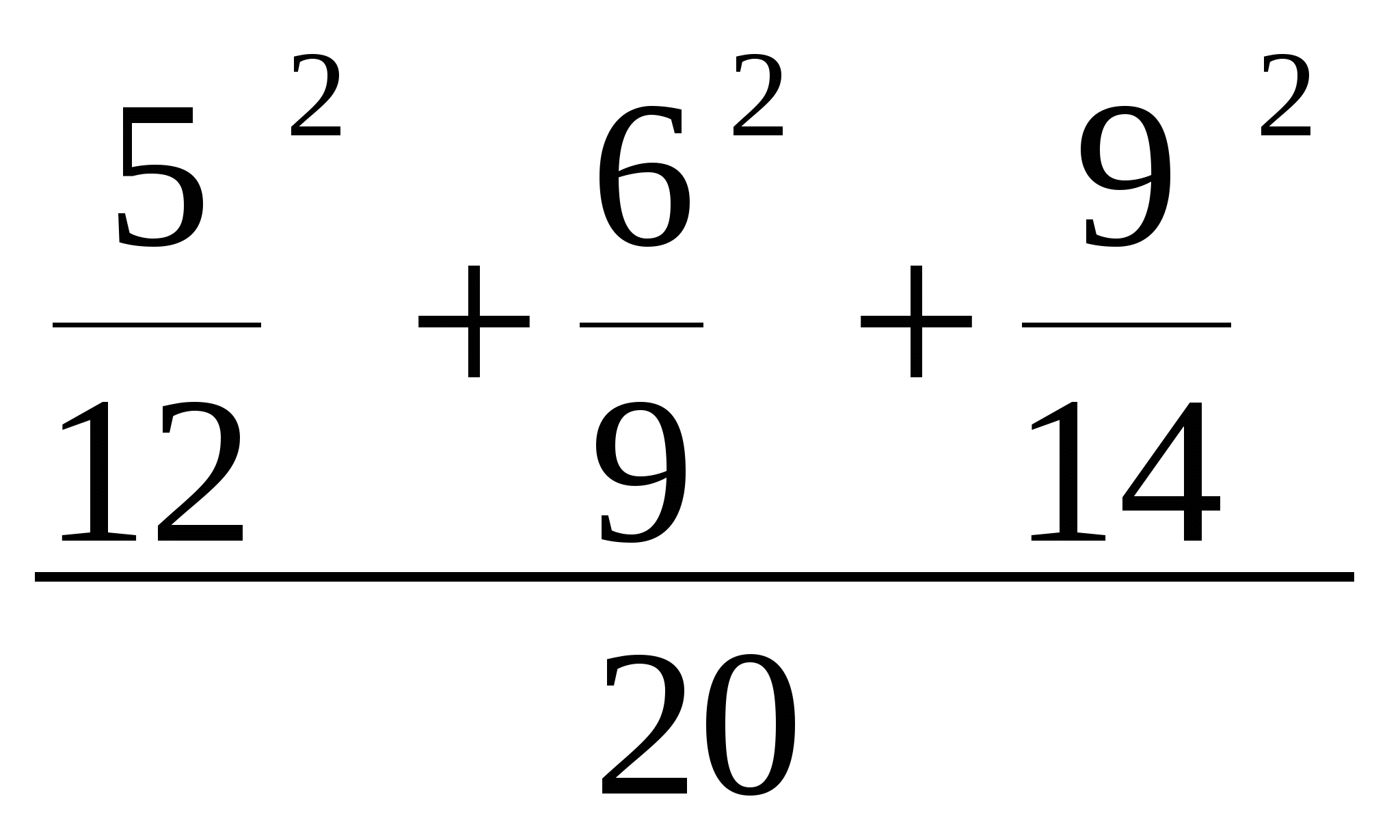 + + 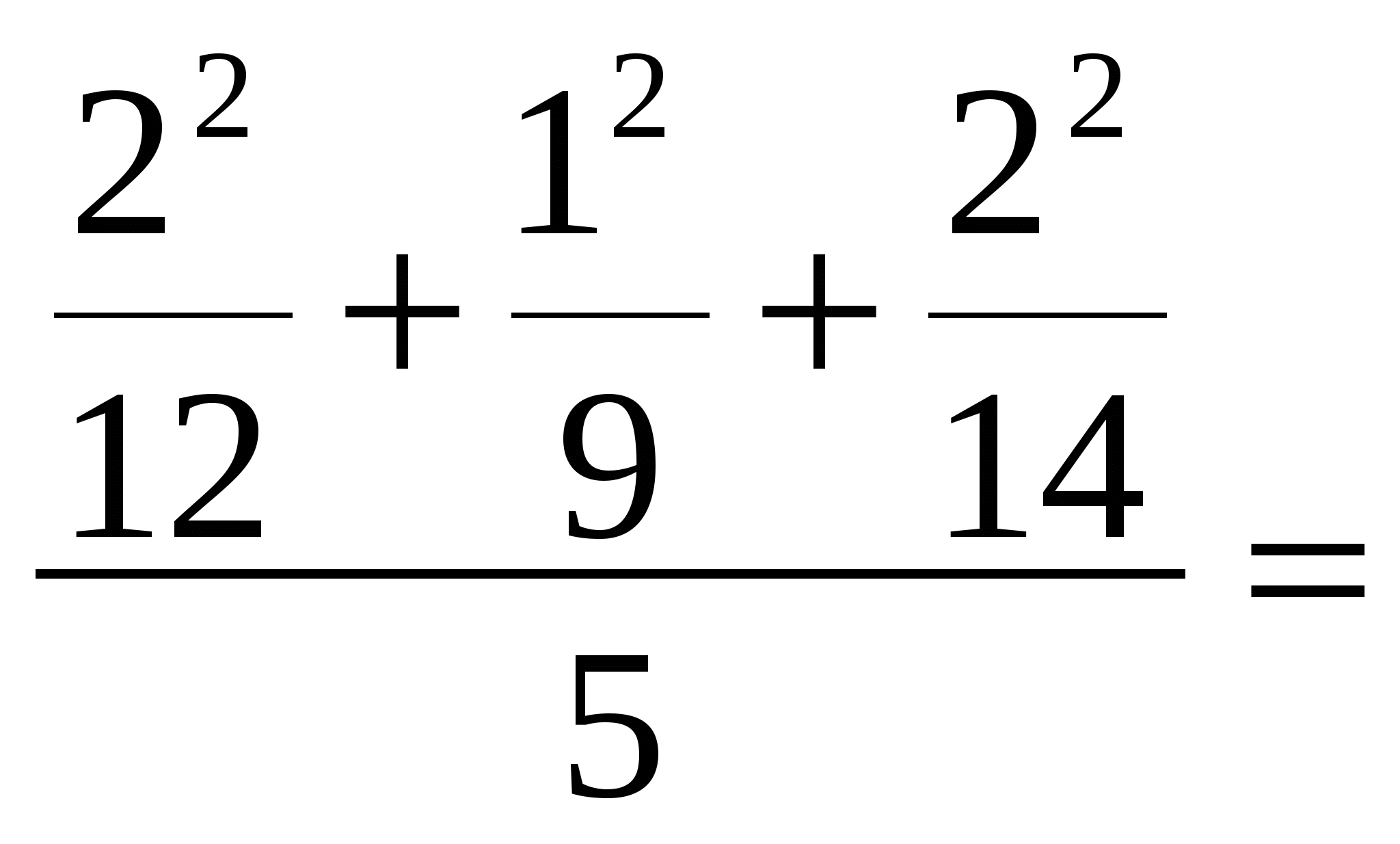 + Кп = Кч = 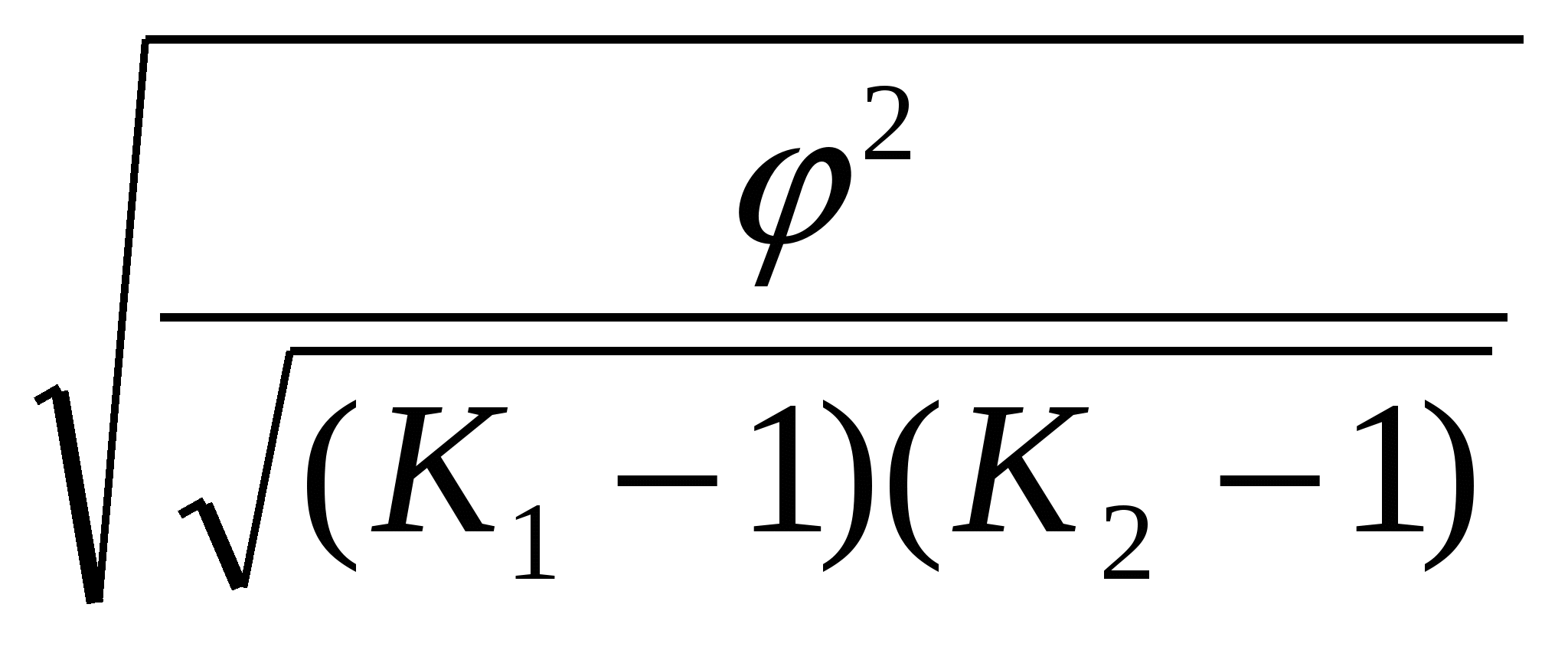 = =Чем Кп и Кч ближе к 1, тем связь сильнее. Вывод: Освоение курса «Статистика» не зависит от типа школы, которую закончили студенты. Для определения тесноты связи как между количественными, так и между качественными признаками при условии, что значения этих признаков могут быть упорядочены (проранжированы) по степени убывания или возрастания признака используют коэффициент корреляции рангов Спирмена, который рассчитывается по формуле: где di – квадраты разности величин x и y. n - число наблюдений (число пар рангов) Используя данные примера 2 по нелинейной корреляционной зависимости, рассчитаем коэффициент Спирмена. Для этого построим таблицу 12. Таблица 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
