Статистика - лекция - Корреляция. Статистическое изучение взаимосвязи социальноэкономических явлений. Корреляционнорегрессионный анализ
 Скачать 0.86 Mb.
|
расчетная таблица
Определим  по специальным таблицам распределения Стьюдента (t – распределение) (v=n-k, где k – число фактических признаков; v= 12-1-1=10) (приложение 3) tk = 2,228.Сравнение фактических и табличных значений t – критерия:  49,75 > 2,228 < 46,0 позволяет признать вычисленные по уравнению (19) параметры типичными. Далее произведем оценку практической значимости синтезированной модели (19). Для криволинейной связи оценка производится посредством индекса корреляции R по формуле (20): 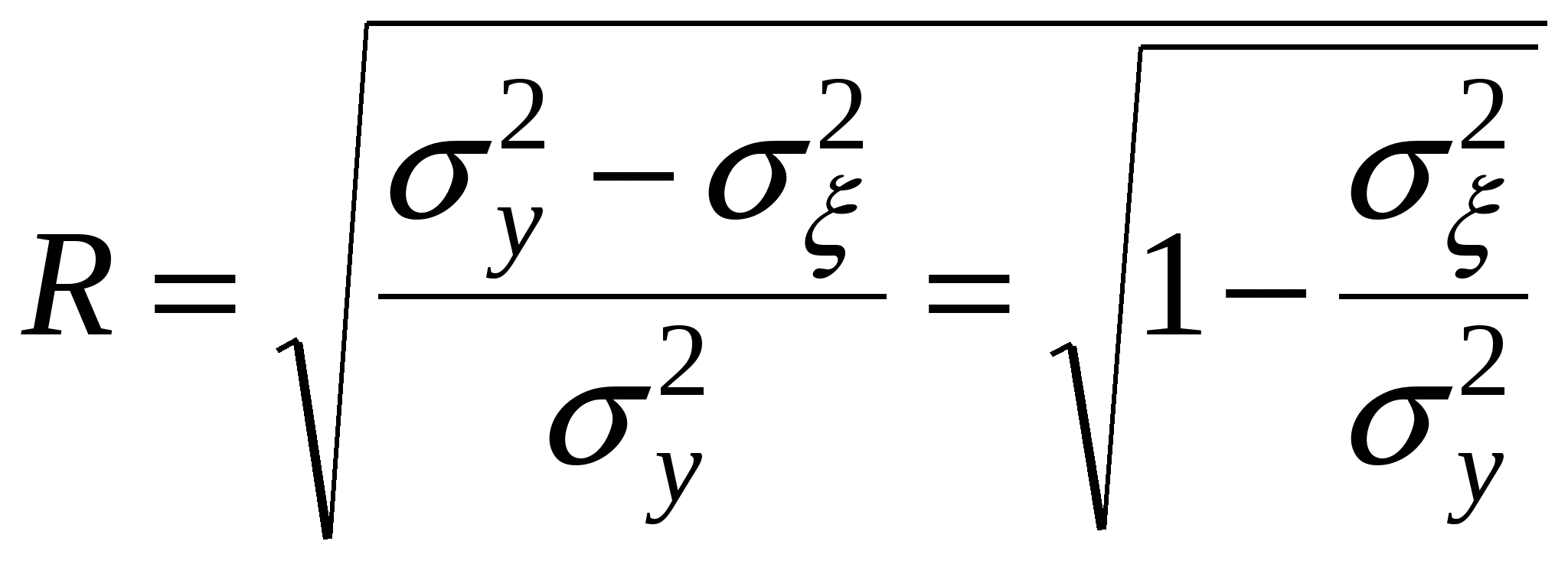 ,где 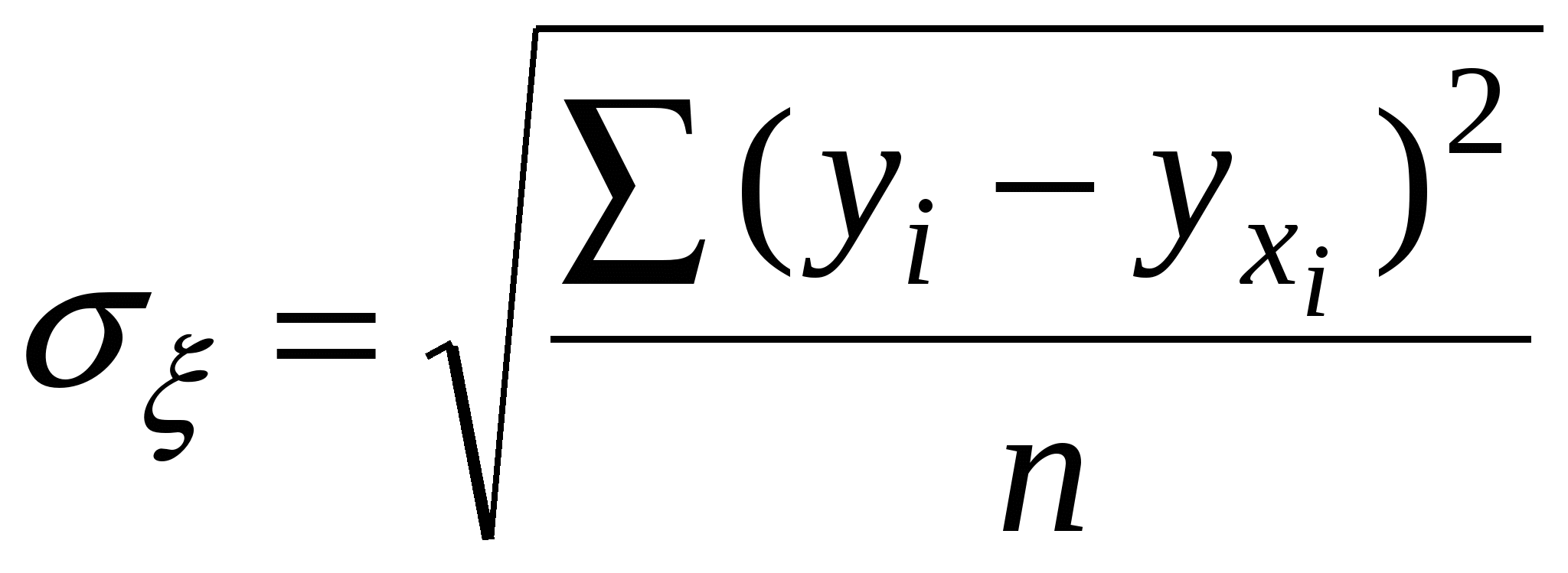 ,    2 =  ;  Определяем индекс корреляции:R =   0,919Полученная величина R = 0,919 означает, что в соответствии со шкалой Чеддока установленная по уравнению регрессии связь между себестоимостью единицы продукции и объёмом произведенной продукции весьма высокая. Оценка значимости коэффициента корреляции R = 0,919 осуществляется по F – критерию Фишера. Фактическое значение критерия FR определяется по формуле  (16)где m – число параметров уравнения регрессии. Величина FR сравнивается с критическим значением Fk, которое определяется по таблице F-критерия с учетом принятого уровня значимости  и числа степеней свободы k2 = m – 1 (знаменатель) и k2 = n – m(числитель).При уровне значимости =0,5 и степенях свободы k2 =2-1=1 и k1 = 12 – 2 = 10, табличное значение Fk = 4,96. 54,35>4,96 , следовательно, величина индекса корреляции признается существенной.R2 – индекс детерминации = 0,9192 =0,8446 или 84,5%. Отсюда следует, что 84,5% общей вариации объясняется изменением факторного признака Х. Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации  .Значение средней ошибки аппроксимации определяется по формуле:  (17)и не должно превышать 12-15%. Среднюю ошибку аппроксимации определим по формуле (17)  Средняя ошибка аппроксимации составляет 11,0%. Поэтому синтезированная по уравнению гиперболы математическая модель (19) может быть использована для практических целей. 4. Множественная регрессия. Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трех и более признаков одновременно, вычисляется множественный и частные коэффициенты корреляции. Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков. Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле:  , гдеrух - парные коэффициенты корреляции между признаками. Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: 0 ≤ R≤1. Приближение Rк единице свидетельствует о сильной зависимости между признаками.    Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками х1 и х2 при фиксированном значении других (k - 2) факторных признаков, то есть когда влияние х1 исключается, то есть оценивается связь между х1 и х2 в "чистом виде". В случае зависимости у от двух факторных признаков х1 и х2 коэффициенты частной корреляции имеют вид:  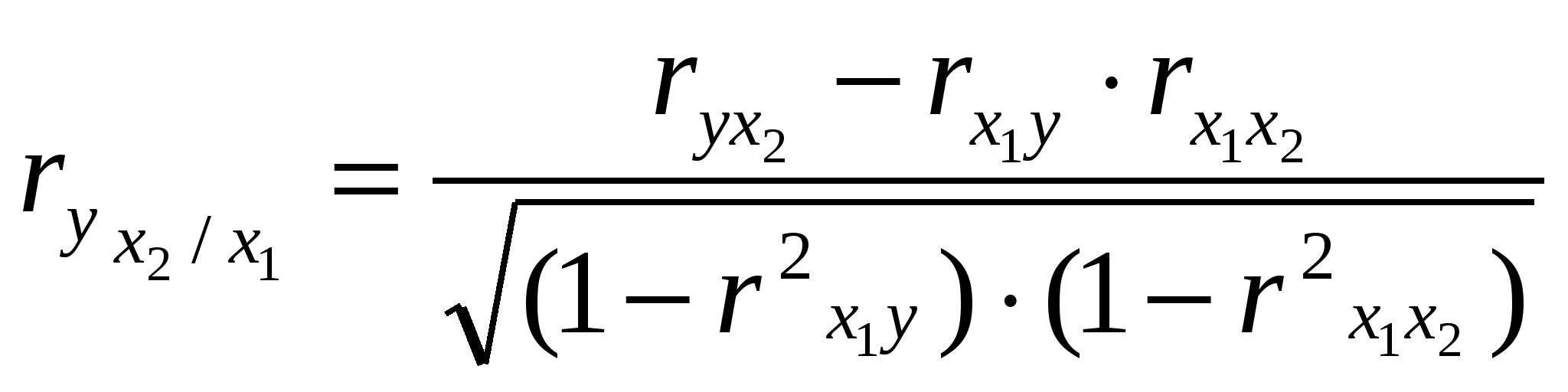 , где r – парные коэффициенты корреляции между указанными в индексе переменными. В первом случае исключено влияние факторного признака х2, во втором – х1. Пример 1. Имеются данные по отдельным областям РФ о естественном убытии (приросте) населения человек за 1994 год в расчете на 1000 жителей (%), численности безработных к экономически активному населению и состояние условий труда работников в % к общей численности занятых на производстве (табл. 6). На основании имеющихся данных определите влияние численности безработных (х1)и занятости работников в условиях, не отвечающим санитарно-гигиеническим нормам (х2)на естественную убыль населения (У) в областях Российской Федерации. Для этого определите: а) параметры уравнения Ух1х2 = а0 + а1х1 + а2х2, использовав метод наименьших квадратов; б) коэффициенты парной корреляции rх1у, rх2у, rх1у г) коэффициент множественной корреляции Rу (Х1Х2); д) тесноту связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов, т.е. определите значения rх1у (х2) и rх2у (х1). Сделайте выводы. Таблица 6 Исходные данные
|
)2
