Статистика - лекция - Корреляция. Статистическое изучение взаимосвязи социальноэкономических явлений. Корреляционнорегрессионный анализ
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
Показатели работы некоторых сельскохозяйственных предприятий Тамбовской области (данные условные)
По данным о фондовооруженности и производительности труда в некоторых предприятиях области необходимо определить направление и тесноту связи между признаками. Данные в таблице 3 представлены после предварительной их обработки методом приведения параллельных данных. Сопоставив полученные ряды данных x и y можно наблюдать наличие прямой зависимости между признаками, когда увеличение фондовооруженности влечет за собой рост производительности труда. Исходя из этого, можно сделать предположение, что связь между признаками прямая, и ее можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа (рис.1). Анализ рис.1 показывает наличие близкой к прямолинейной зависимости так как точки расположены практически по прямой линии. Прямолинейная форма зависимости у от х описывается уравнением прямой: 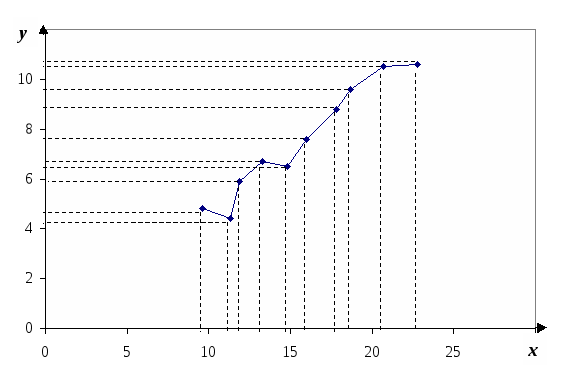 Рис. 1. Зависимость производительности труда в некоторых сельскохозяйственных предприятиях области от фондовооруженности, тыс. руб. Определим параметры уравнения прямой на основе метода наименьших квадратов. Исходные данные и расчетные показатели представлены в таблице 3. 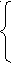  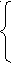 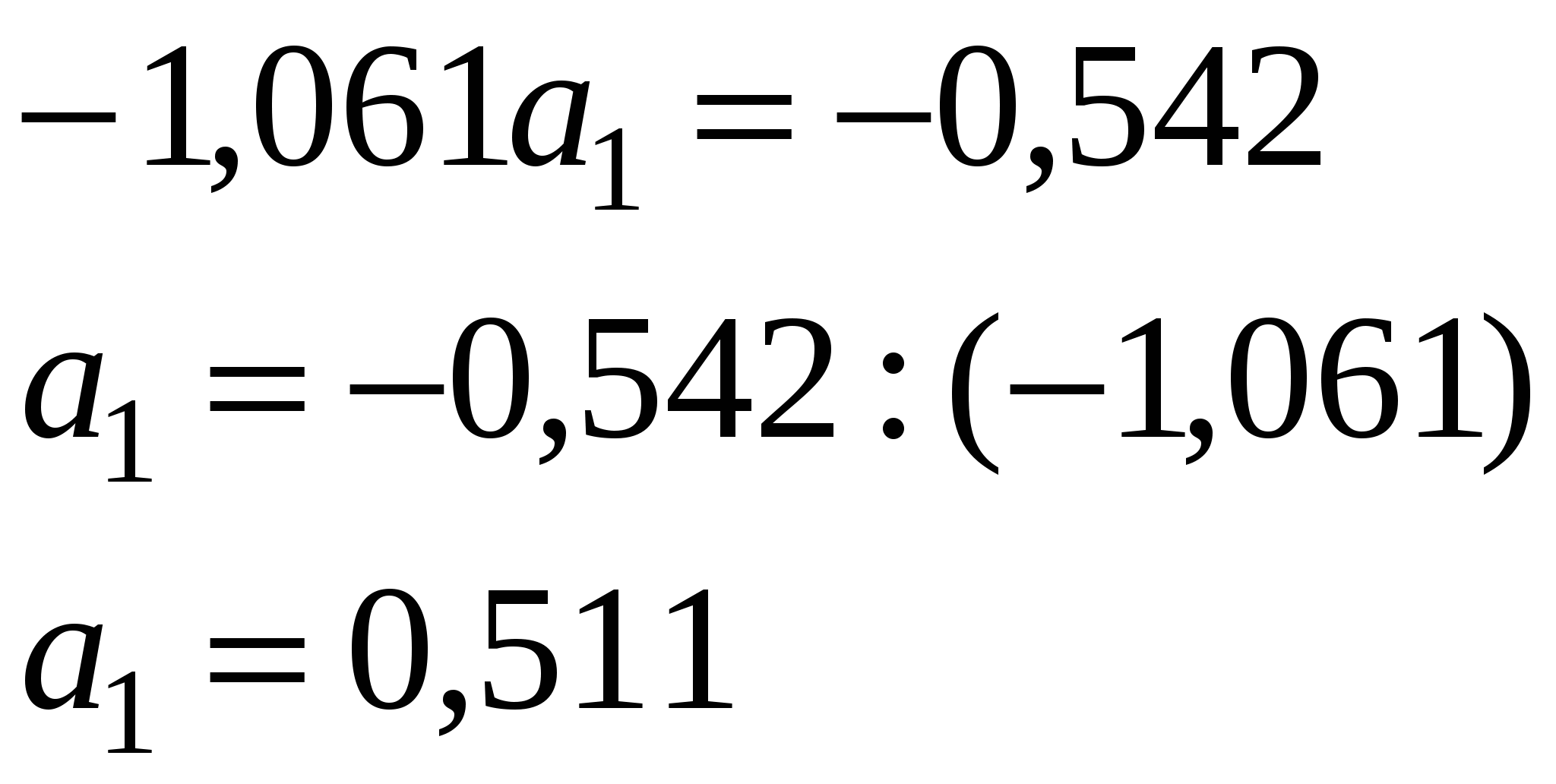 ТТаблица 3 расчетная таблица
Далее 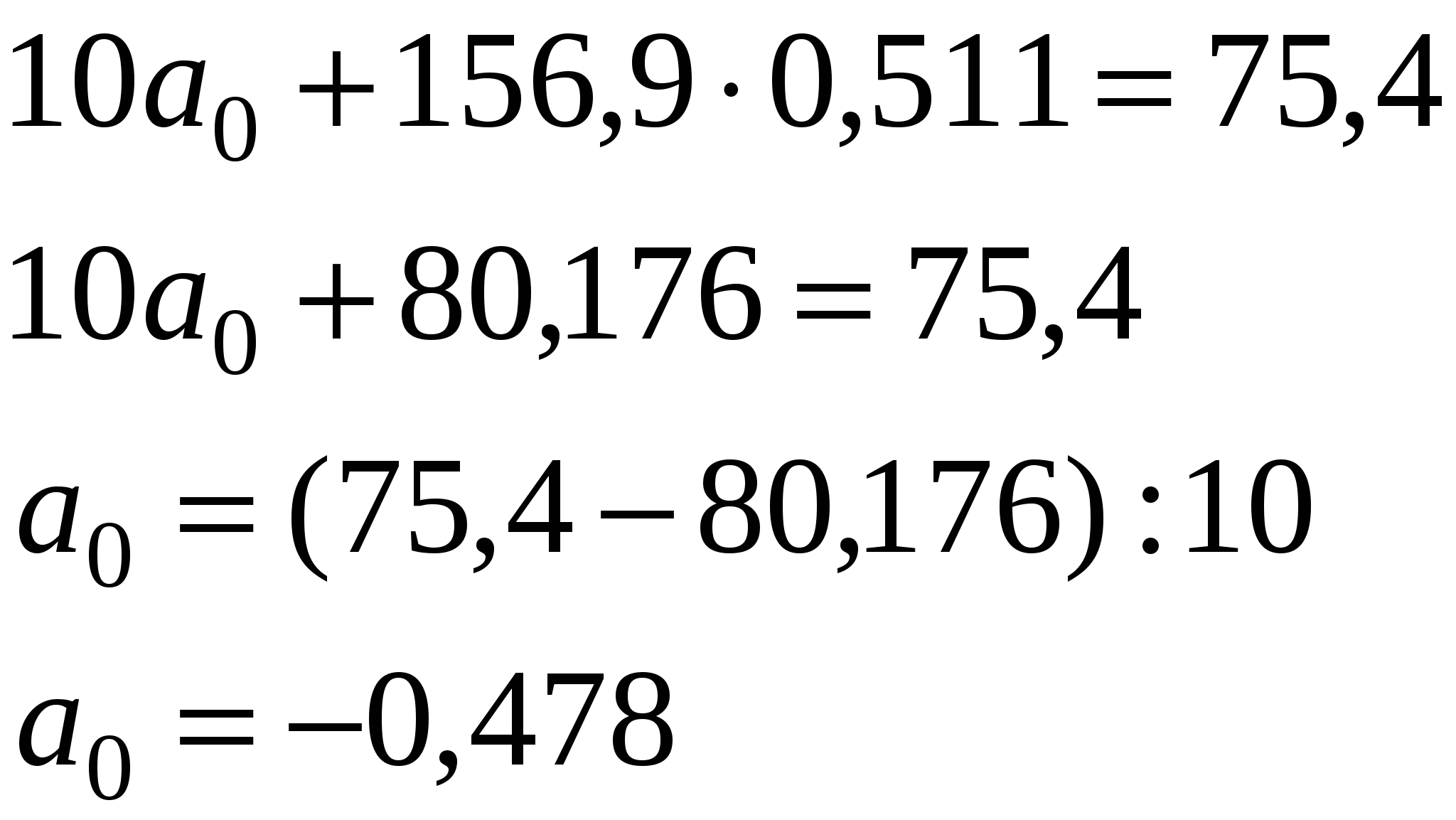 Уравнение прямой: Отсюда: Параметры уравнения а0 и а1 можно также вычислить по следующим формулам 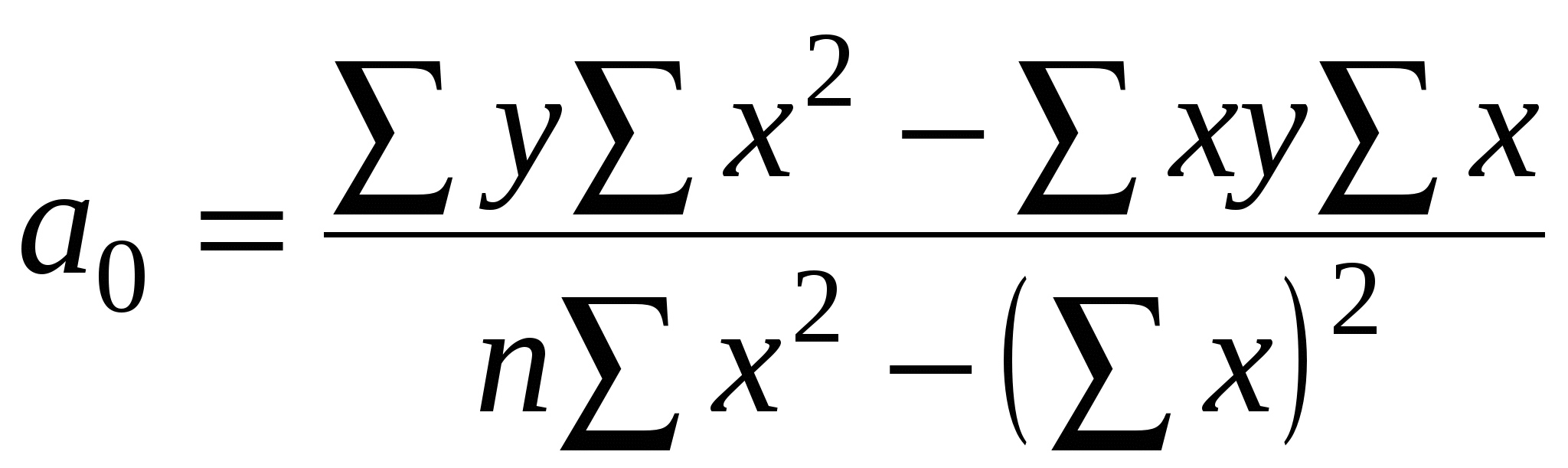 В уравнении регрессии параметр а0 показывает усреднённое влияние на результативный признак неучтённых (невыделенных для исследования) факторов; параметр а1 = 0,511 – коэффициент регрессии показывает, что с увеличением фондовооруженности труда на 1 тыс. рублей, производительность труда возрастает на 0,511 тыс. руб. Проверим параметры данного уравнения на типичность. Для этого, используя формулы (3), (4), (5), (6), рассчитаем необходимые данные. 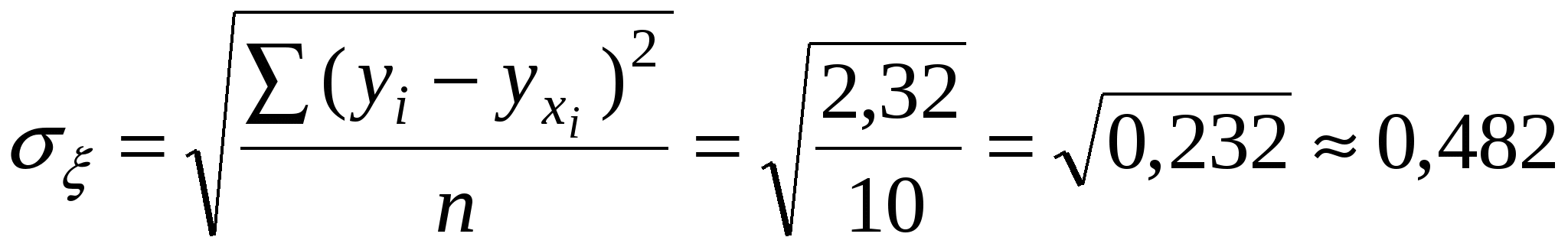 Определим Сравнение фактических и табличных значений t – критерия: позволяет признать вычисленные по уравнению параметры: а0 – нетипичным, а1 - типичным. Далее произведем оценку практической значимости синтезированной модели 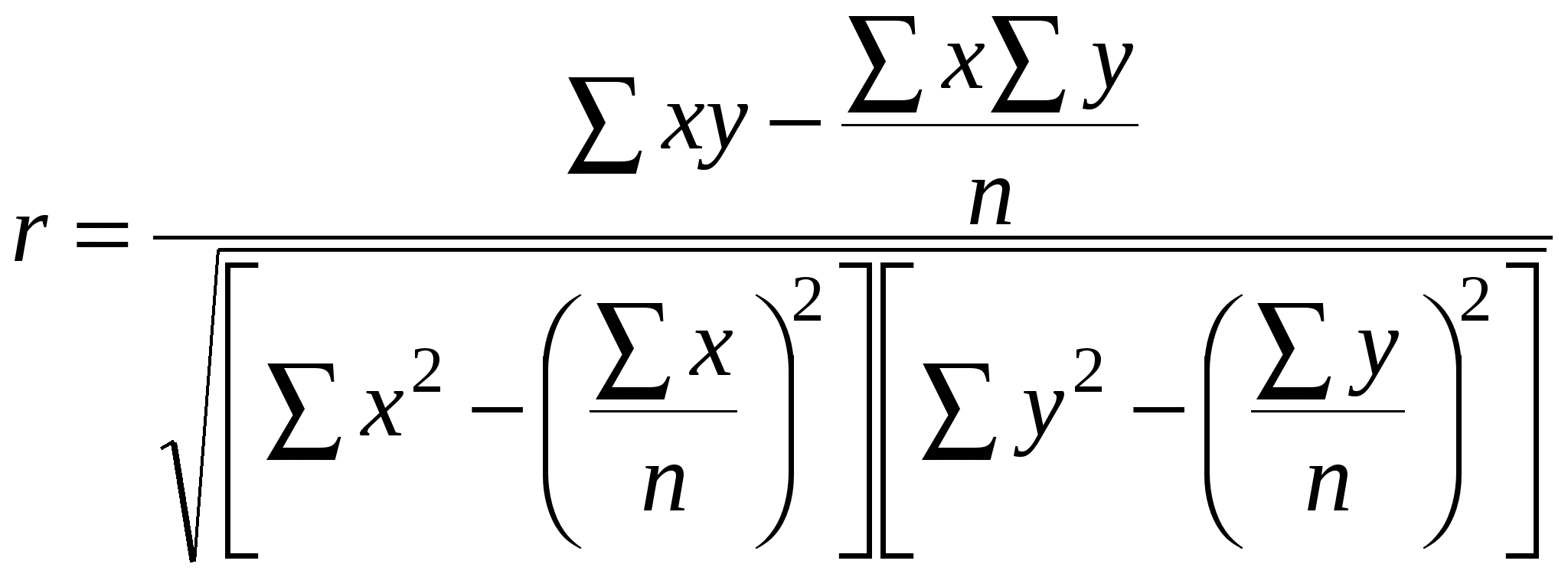 определяем значение r. определяем значение r.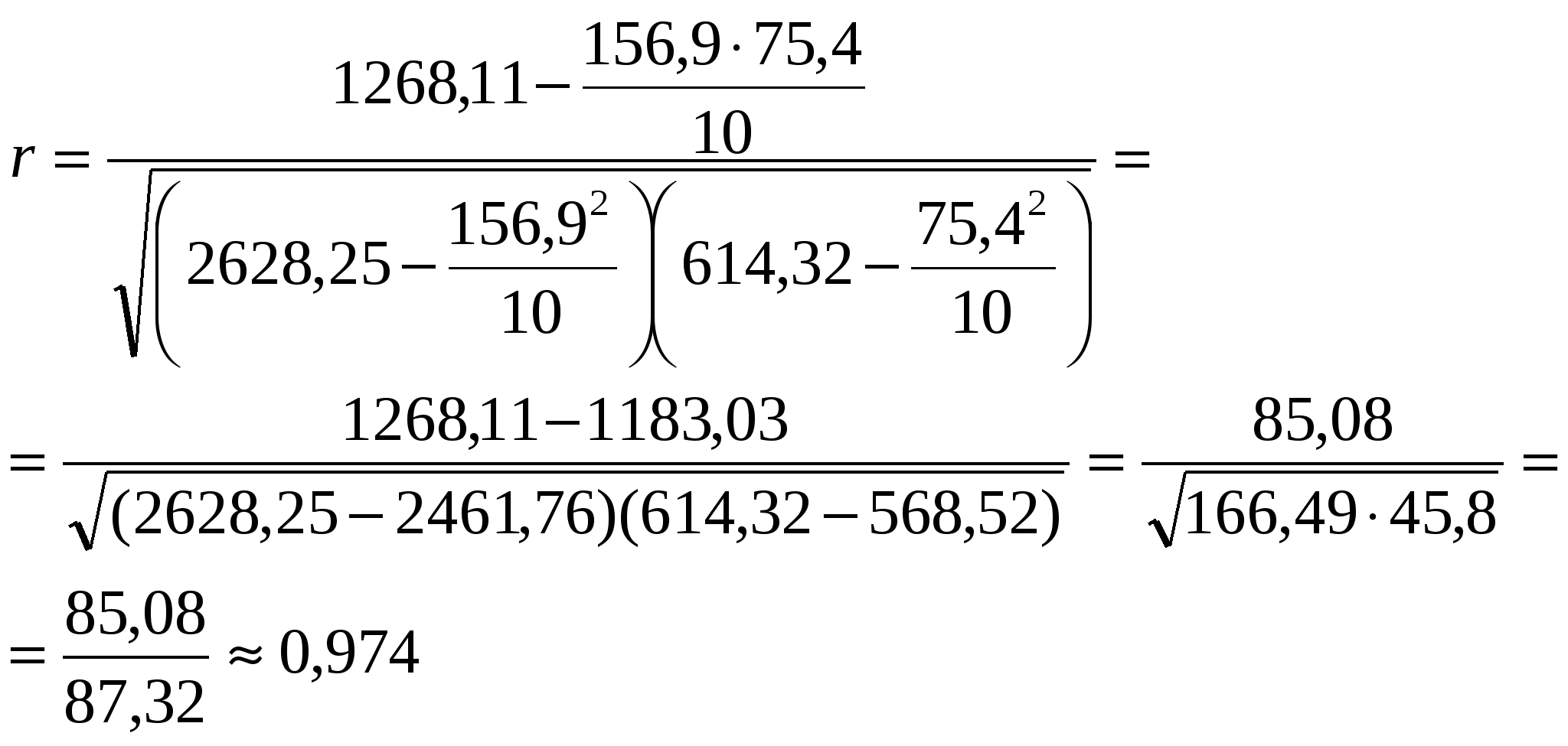 Полученная величина r = 0,974 означает, что в соответствии со шкалой Чеддока (стр. 147 данного пособия) установленная по уравнению регрессии связь между фондовооруженностью и производительностью труда весьма высокая. Оценка значимости коэффициента корреляции осуществляется по t – критерию. Фактическое значение этого критерия tr определяется по формуле При критическом значении tk =2,306 получается, что tr > tk. Поэтому вычисленный коэффициент корреляции признается существенным. Среднюю ошибку аппроксимации определили по формуле: Средняя ошибка аппроксимации составляет 6,6%. Из значения r2 = 0,9742 = 0,949 следует, что 94,9% общей вариации объясняется изменением факторного признака. Коэффициент эластичности определим по формуле: где ai - коэффициент регрессии при соответствующем факторном признаке. Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%. Таким образом, построенная нами модель зависимости У от Х
Пример 2. Используя данные таблицы 4, выявите характер связи между факторными и результативными признаками. Изобразите корреляционную связь графически. Измерьте тесноту связи с помощью коэффициента корреляции. Постройте адекватное уравнение регрессии, рассчитайте коэффициент Фишера и ошибку аппроксимации. Таблица 4 |
