Методичка по статистики. Статистическая сводка и группировка. Статистические таблицы
 Скачать 0.79 Mb.
|
 Таблица 14 Таблица исходных данных и расчетных данных (цифры условные)
Пояснения к таблице. Первые две графы - исходные уровни ряда динамики дополняются графой, в которой показана система отсчета времени "t". Причем эта система выбирается таким образом, чтобы  Если число уровней ряда четное, то вместо нуля в центре мы поставили бы единицы с противоположными знаками у двух уровней, находящихся в середине ряда. Тогда разница между годами составляла бы две единицы времени, и общий вид систем был бы таким (например, для ряда из 6 уровней): 1990 1991 1992 1993 1994 1995 -5 -3 -1 +1 +3 +5 В случае применения упрощенной системы отсчета времени параметры уравнения находятся по упрощенным формулам:   Таким образом, уравнение, выражающее тенденцию роста выплавки чугуна, имеет вид:  На основе этого уравнения находятся выравненные годовые уровни путем подстановки в него соответствующих значений "t" (они показаны в последней графе таблицы, причем общий объем выплавки чугуна остался неизменным). Вопросы для самопроверки 1. В чем состоит значение рядов динамики в экономико-статистическом исследовании? 2. Каковы принципы и правила построения рядов динамики? 3. Какие различают виды рядов динамики? 4. Как исчисляется средняя хронологическая интервальных и моментных рядов динамики? 5. Что такое абсолютный уровень ряда динамики, темп роста, абсолютный и относительный прирост, средний темп роста? 6. Какие Вы знаете методы выявления основной тенденции ряда динамики? 7. Какая разница между механическим сглаживанием и аналитическим выравниванием? 8. Что показывают индексы сезонности и как они исчисляются? Задания для самостоятельной работы Задача 1. Вычислите цепные и базисные абсолютное приросты, темпы роста и прироста, а также абсолютные значения 1% прироста по следующим данным:
Задача 2. По данным задачи N1 рассчитайте средние показатели ряда динамики за 1991-1996 гг.: средний валовой сбор, средний абсолютный прирост валового сбора, средний темп роста и прироста. Задача 3. По данным задачи N1 произведите аналитическое выравнивание ряда динамики по уравнению прямой и с помощью трехчленной скользящей средней. Задача 4. Темпы роста выпуска изделия "А" в отрасли составили: в 1994 г. - 101%, 1995 г. - 103%, 1996 г. - 84%. Определите средний годовой темп прироста за 1994-1996 гг. Ответ: 2,9%. Задача 5. Исчислите средние товарные запасы за I и II кварталы и за полугодие в целом по нижеследующим данным:
Ответ: 22,2; 24,6; 23,4 млн.руб. Задача 6. На основании приведенных данных сделайте анализ внутригодовой динамики о реализации картофеля на рынках города; выявите сезонность покупательского спроса на эти продукты, предварительно выравнив ряд по прямой (тыс. ц): (цифры условные)
Ответ: 108,3%; 101,5%; 96,1%; 99,1%; 87,9%; 83,8%; 88,3%; 96,9%; 99,9%; 107,9%; 115,1%; 123,2%. Задача 7. Произведите обработку ряда динамики закупок картофеля в области методом: а) укрупнения интервалов; б) скользящей средней:
ЭКОНОМИЧЕСКИЕ ИНДЕКСЫ Экономический индекс - это относительная величина, которая характеризует изменение исследуемого явления во времени, в пространстве, или по сравнению с некоторым эталоном (планируемым, нормативным уровнем и т.п.). Если в качестве базы сравнения используется уровень за какой-либо предшествующий период - получают динамический индекс, если же базой является уровень того же явления по другой территории - территориальный индекс. Индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или в пространстве две совокупности, элементы которых являются несоизмеримыми величинами. Изучение данной темы должно базироваться, на знании предшествующих разделов курса и, в особенности тем "Теория статистических показателей" и "Статистическое изучение динамики социально-экономических явлений". Индексы могут быть индивидуальными и сводными. Индивидуальные индексы характеризуют изменение исследуемого показателя по одному товару или виду продукции. Сводные индексы отражают общее изменение по товарной группе или продуктовому ряду предприятия. Сводный индекс цен может исчисляться в агрегатной, среднеарифметической или среднегармонической формах. Например для индекса цен имеем: агрегатный - 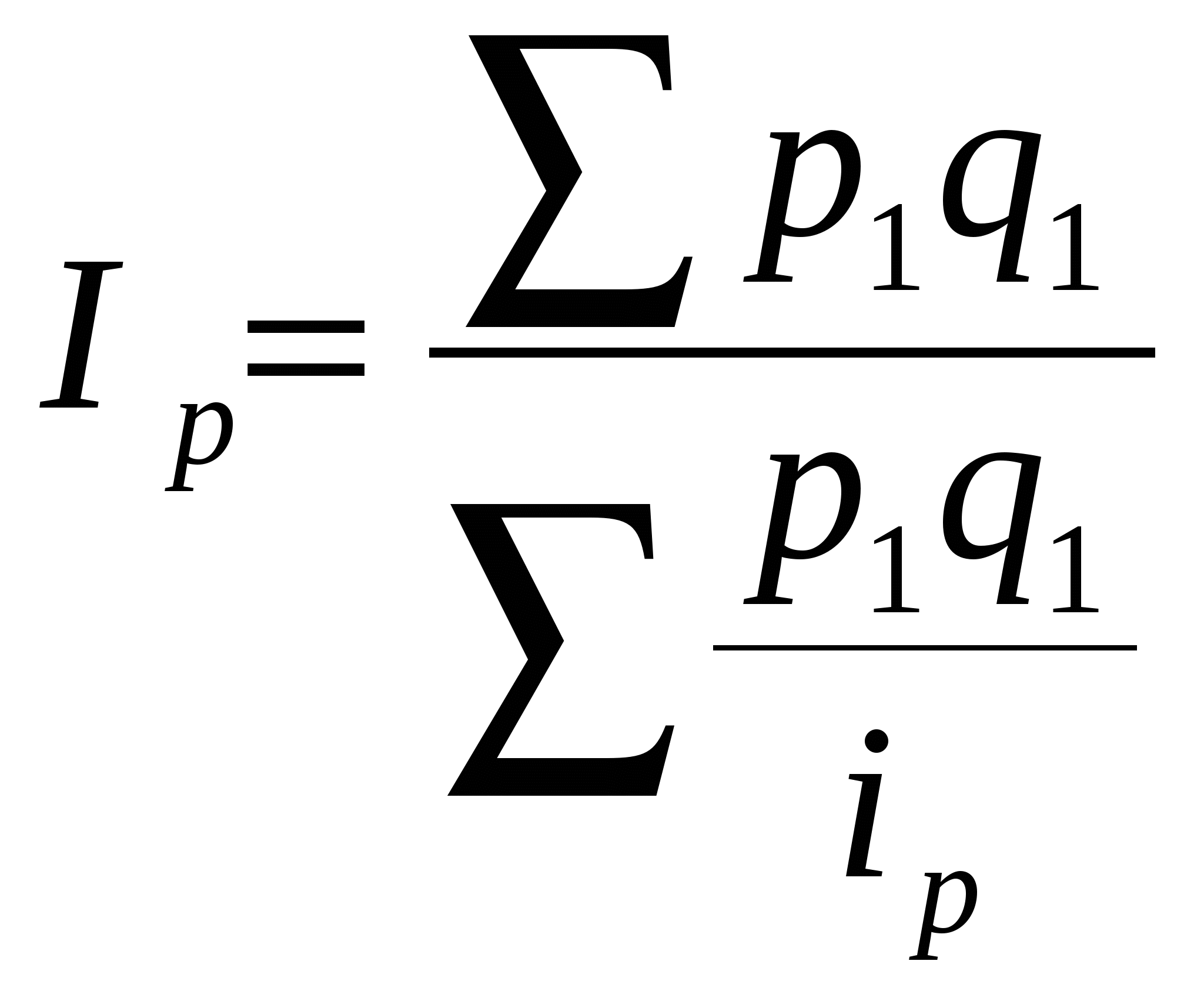 , (где  -цены,  - количество товара) среднеарифметический - , среднегармонический -  , Специфическим вопросом построения индексов является выбор весов. Так, при расчете сводного индекса цен, текущие и базисные цены на товары, в большинстве случаев «взвешиваются» по объему реализации текущего периода (как это сделано выше), но иногда могут использоваться и базисные веса. Необходимо уяснить, что выбор весов в одном индексе обуславливает их выбор во всех взаимосвязанных с ним индексах. Приведем примеры индексных расчетов. Пример1. Рассчитать индивидуальные и общие индексы товарооборота, физического объема проданных товаров и цен по следующим данным о ценах и реализации (товаров) за два месяца: Таблица 14
Индивидуальные индексы, характеризующие динамику показателей по каждому товару, помещены в графах 7, 8, 9 таблицы по строкам А, Б, В. Они легко получаются путем сравнения соответствующих показателей за январь и февраль (например, индекс цен по товару "А" равен  . Сводные индексы записаны по итоговой строке этих колонок. Они рассчитаны следующим образом:  Полученный результат указывает на то, что цены снизились на 12.3%.Из формулы следует, что индекс цен есть отношение стоимости товаров отчетного периода к стоимости тех же товаров, но по базисным (у нас январским) ценам. Снижение цен привело к удешевлению массы товаров, проданных в феврале в абсолютном выражении на сумму 1300 руб. (10600-9300). Индекс количества проданных товаров (физического объема товарооборота) рассчитывается как отношение товарооборота отчетного периода по базисным ценам к товарообороту базисного периода:  Следовательно, физический объем продажи возрос на 2,7%. Индекс товарооборота (стоимости проданных товаров) может быть получен двумя способами: 1 ) по формуле  2) на основе рассчитанных индексов  Если индексы рассчитываются за три и более периода, то в зависимости от задач исследования и имеющихся данных выбирают один из четырех возможных вариантов построения индексной системы: цепные индексы с переменными или постоянными весами, базисные индексы с переменными или постоянными весами. Для изучения динамики среднего уровня в статистике используют систему взаимосвязанных индексов, которая включает в себя индекс переменного состава, индекс фиксированного (постоянного) состава, индекс структурных сдвигов. Данные индексы позволяют определить, как изменится средняя величина за счет изменения индивидуальных значений признака и за счет изменения структуры производства или реализации. Индекс переменного состава определяется по формуле | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(млн.т)