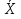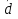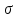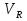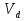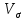СМ в УК.РГЗ. Статистические характеристики случайных величин
 Скачать 270.11 Kb. Скачать 270.11 Kb.
|
 Статистические характеристики случайных величин Статистические характеристики случайных величинЗадание 1 1.1 Построить вариационный ряд распределения непрерывной случайной величины в виде гистограммы по заданным в таблице значениям. Исходные данные:
Вариационный ряд распределения непрерывной случайной величины:
Представим вариационный ряд распределения непрерывной случайной величины в виде гистограммы: Рис.1 – Вариационный ряд распределения непрерывной случайной величины. 1.2 Определить: среднее арифметическое, моду, медиану; абсолютные и относительные показатели вариации: размах; среднее линейное отклонение; дисперсию; среднее квадратическое отклонение; коэффициент осцилляции; коэффициент вариации; линейный коэффициент вариации. Определим средневзвешанное значение:
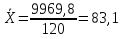 ; ;Определим моду: 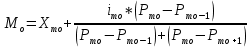 ; ;где 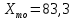 ; ;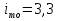 ; ;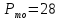 ; ;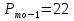 ; ;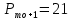 ; ;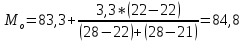 ; ;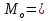 84,8; 84,8;Определим медиану: 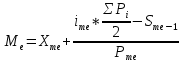 ; ;Где 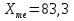 ; ;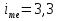 ; ;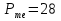 ; ;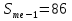 ; ;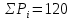 ; ;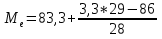 =76,6; =76,6;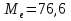 ; ;Найдем абсолютные и относительные показатели вариации: 1.Размах: R= Xmax- Xmin; R=36,3; 2.Среднее линейное отклонение: 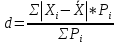 ; ;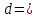 0,57; 0,57;3.Дисперсия: 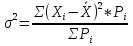 ; ;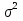 =338,6; =338,6;4.Среднеквадратическое отклонение: 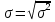 ; ;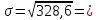 18,4; 18,4;5.Коэффициент осциляции: 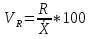 ; ;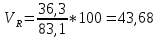 ; ;6.Коэффициент вариации: 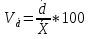 ; ;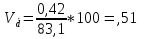 ; ;7.Линейный коэффициент вариации: 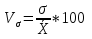 ; ;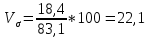 ; ;1.3 Произвести 20%-ную выборку из данной генеральной совокупности (колонки Х1–Х3, табл. А.1) с помощью таблицы случайных чисел. Для полученной выборки рассчитать среднее арифметическое значение, абсолютные и относительные показатели вариации. Произвели 20%-ную выборку:
Рассчитали среднее арифметическое значение, абсолютные и относительные показатели вариации:
R=99,8-74,3=25,5;
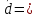 0,04; 0,04;
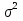 =0,2; =0,2;
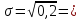 0,45; 0,45;
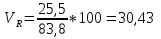 ; ;
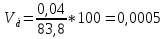 ; ;
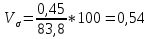 ; ;1.4 Результаты выполненной статистической обработки оформили в виде таблицы. Таблица 1 Результаты статистической обработки данных
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

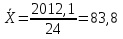 ;
;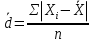 ;
;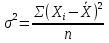 ;
;