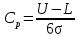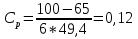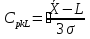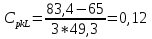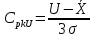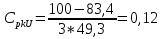СМ в УК.РГЗ. Статистические характеристики случайных величин
 Скачать 270.11 Kb. Скачать 270.11 Kb.
|
|
Интервальное оценивание Интервальное оценивание математического ожидания случайной величины выполняется в соответствии с алгоритмами, приведенными в п. 6.1 и 6.2 ГОСТ Р 50779.21. Исходные данные для выполнения задания приведены в Приложении А методических указаний (колонка Х2). Для нахождения промежуточных значений квантилей распределения Стьюдента необходимо применить метод линейной интерполяции (Приложение Б, ГОСТ Р 50779.21). Задание №2 2.1 Произвести точечное и интервальное оценивание математического ожидания генеральной совокупности:
Уровень доверия принять 0,95. Исходные данные:
При известном значении дисперсии: 1.Статистические и исходные данные: -объем выборки:n=40; -сумма значений наблюдаемых величин: 3305,1; -известное значение дисперсии 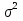 = 0,2; = 0,2;-выбранная доверительная вероятность: 1- 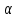 =0,95; =0,95;2. Табличные данные и вычисления: -квантиль стандартного нормального распределения уровня 1- 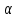 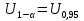 ; ;Для 0,95 по табл. Приложения А.1 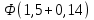 ; ;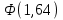 ; ;-квантиль стандартного нормального распределения уровня 1- 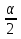 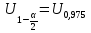 ; ;Для 0,975 по табл. Приложения А.1 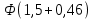 ; ;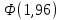 ; ;-вычислим среднее арифметическое 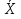 : :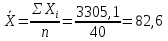 ; ;-вычислим 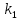 (для одностороннего интервала): (для одностороннего интервала):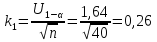 ; ;-вычислим 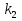 (для двухстороннего интервала): (для двухстороннего интервала):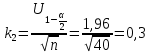 ; ;3.Результаты -точечная оценка математического ожидания, 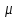 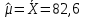 ; ;-двусторонний симметричный доверительный интервал для 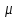 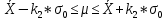 ; ;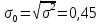 ; ;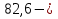 0,3*0,45 0,3*0,45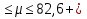 0,3*0,45; 0,3*0,45;82,5 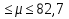 ; ;-односторонние доверительные интервалы для 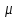
При неизвестном значении дисперсии: 1.Статистические и исходные данные: -объем выпорки: n=40; -сумма значений наблюдаемых величин: 3305,1; -сумма квадратов значений наблюдаемых величин 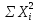 ; ;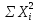 =247176,6; =247176,6;-степень свободы 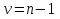 ; ;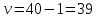 ; ;-выбранная доверительная вероятность: 1- 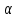 =0,95; =0,95;2. Табличные данные и вычисления: -квантиль распределения Стьюдент (t) уровня 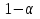 с с 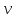 степенями свободы по табл.Приложения Б.1 ГОСТ Р 50779.21-2004 степенями свободы по табл.Приложения Б.1 ГОСТ Р 50779.21-2004Для нахождения промежуточных значений квантилей распределения Стьюдента необходимо применить метод линейной интерполяции:
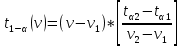 + +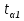 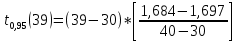 +1,697=-0,0117+1,697=1,685; +1,697=-0,0117+1,697=1,685;-квантиль распределения Стьюдента (t) уровня 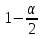 с с 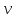 степенями свободы по табл.Приложения Б.1 ГОСТ Р 50779.21-2004 степенями свободы по табл.Приложения Б.1 ГОСТ Р 50779.21-2004Для нахождения промежуточных значений квантилей распределения Стьюдента необходимо применить метод линейной интерполяции:
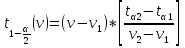 + +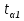 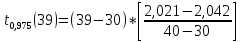 +2,042=-0,0189+2,042=2,023; +2,042=-0,0189+2,042=2,023;-вычислим среднее арифметическое 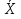 : :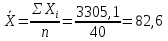 ; ;-вычислим дисперсию 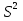 : :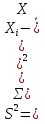 ; ;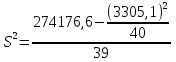 = =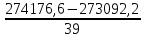 =27,8; =27,8;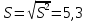 ; ;-вычислим коэффициент 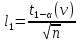 ; ;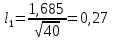 ; ;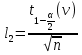 ; ;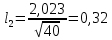 ; ;3. Результаты: -точечная оценка математического ожидания 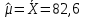 ; ;-точечная оценка генеральной совокупности 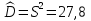 ; ;-двусторонний симметричный доверительный интервал 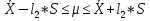 ; ;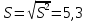 ; ;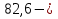 0,32*5,3 0,32*5,3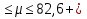 0,32*5,3; 0,32*5,3;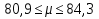 ; ;-односторонние доверительные интервалы для 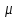
Законы распределения случайных величин Выполнение этого задания РГЗ заключается в решении задач по определению вероятности обнаружения несоответствующих единиц продукции в выборке с применением разных законов, описывающих распределение исследуемого параметра в генеральной совокупности. Задание №3 3.1 Определить вероятность обнаружения ноль, одного, двух и трех несоответствующих изделий в выборке, используя гипергеометрическое распределение, если заданы объем партии, число несоответствующих изделий в партии и объем выборки. Результаты представить графически – в виде зависимости рассчитанной вероятности обнаружения несоответствующих изделий в выборке Pот числа несоответствий m. Определить математическое ожидание и дисперсию. Исходные данные:
Формула гипергеометрического распределения: 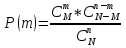 ,где ,где 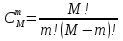 ; ;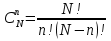 ; ;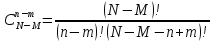 ; ;Для m=0 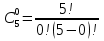 = =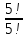 =1 =1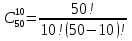 = =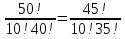 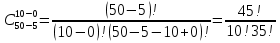 ; ;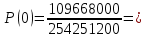 0,31; 0,31;Для m=1 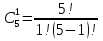 = =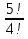 =5 =5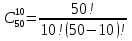 = =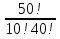 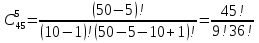 ; ;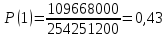 ; ;Для m=2 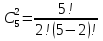 = =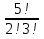 =10 =10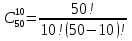 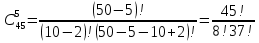 ; ;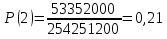 ; ;Для m=3 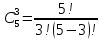 = =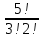 =10 =10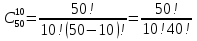 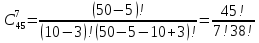 ; ;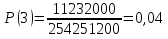 ; ;Полученные данные занесли в таблицу:
Рис.2. Зависимость вероятности обнаружения несоответствующих изделий. Определим математическое ожидание и дисперсию. Математическое ожидание: 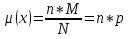 ; ;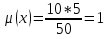 ; ;Дисперсию находим по формуле: 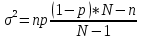 ; ;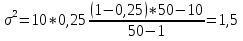 ; ;Среднее квадратическое отклонение: 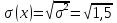 =1,2; =1,2;3.2 Используя биномиальное распределение, определить вероятность обнаружения ноль, одного и двух несоответствующих изделий, если заданы уровень несоответствий в партии (в виде процента несоответствующих изделий) и объем выборки. Результаты представить графически – в виде зависимости рассчитанной вероятности обнаружения несоответствующих изделий в выборке P от числа несоответствий m. Определить математическое ожидание и дисперсию. Исходные данные:
Формула биноминального распределения: 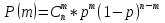 ; ;Где 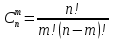 ; ;Для m=0 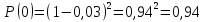 ; ;Для m=1 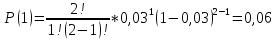 ; ;Для m=2 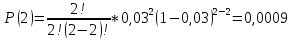 ; ;Полученные данные занесли в таблицу:
Рис.3. Зависимость вероятности обнаружения несоответствующих изделий. Определим математическое ожидание и дисперсию. Математическое ожидание: M(x) = n*p=2*0,03=0,06; Дисперсию находим по формуле: 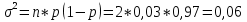 ; ;Среднее квадратическое отклонение: 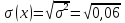 =0,24; =0,24;3.3 Используя распределение Пуассона, определить вероятность обнаружения ноль, одного, двух и трех несоответствующих изделий в выборке, если заданы объем партии, объем выборки и количество несоответствующих изделий в партии. Результаты представить графически – в виде зависимости рассчитанной вероятности обнаружения несоответствующих изделий в выборке P от числа несоответствий m. Определить математическое ожидание и дисперсию. Исходные данные:
Формула распределения Пуассона: 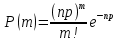 , где , где 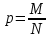 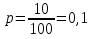 ; ;Для m=0 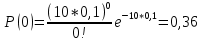 ; ;Для m=1 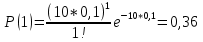 ; ;Для m=2 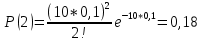 ; ;Для m=3 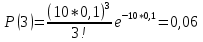 ; ;Полученные данные занесли в таблицу:
Рис.4. Зависимость вероятности обнаружения несоответствующих изделий. Определим математическое ожидание и дисперсию. M(x) = 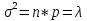 ; ;M(x) = 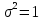 ; ;3.4 Проверить гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона Хи-квадрат. Исходные для выполнения задания приведены выше. Результаты расчетов (теоретические частоты) отразить на графике гистограммы распределения исходных данных.
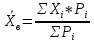 =81,4; =81,4;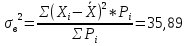 ; ;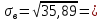 5,99; 5,99;По таблице критических точек распределения 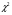 , по уровню значимости α=0,05 и числу степеней свободы k=s–3= 11-3=8 находим критическую точку правосторонней критической области. , по уровню значимости α=0,05 и числу степеней свободы k=s–3= 11-3=8 находим критическую точку правосторонней критической области.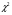 кр = 2,73; кр = 2,73;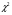 набл = 37,0. набл = 37,0.Так как 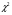 набл> набл>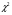 кр – гипотезу о нормальном распределении генеральной совокупности отвергаем. В результате нахождения двух величин видим, что эмпирические и теоретические частоты различаются значимо (рисунок 5). кр – гипотезу о нормальном распределении генеральной совокупности отвергаем. В результате нахождения двух величин видим, что эмпирические и теоретические частоты различаются значимо (рисунок 5).Рис.5. Гистограмма распределения исследуемой величины с эмпирическими и теоретическими частотами. Контрольные карты Задание 4 Задание 4.1
Ход решения
Таблица 18 – Расчетные данные для построения Карты средних и размахов
Вычисляются контрольные границы для контрольной карты средних значений 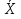 : :
Наносим на график контрольные границы и полученные точки. Контрольные карты средних значений и размахов представлены на рисунке и рисунке 6 и 7. Рис.5. Контрольная карта средних значений( 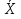 ) )Рис.6 – Контрольная карта размахов(R) Контрольная карта средних и размахов показала, что процесс находится в статистически-управляемом состоянии. Основываясь на типовых структурах особых причин, приведенных в ГОСТ Р ИСО 7870-2-2015, можно сказать, что процесс стабилен, так как значения показателей не выходят за пределы допустимых значений.
Доля несоответствующих единиц продукции была найдена по таблице 3 пункта 5.8 (ГОСТ Р 50779.46-2012). Для 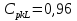 доля несоответствующих единиц равняется 0,3594. Такой результат очевиден, так как карты иллюстрируют стабильный процесс. доля несоответствующих единиц равняется 0,3594. Такой результат очевиден, так как карты иллюстрируют стабильный процесс.Задание 4.2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

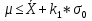 ;
;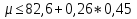 ;
;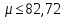 ;
;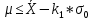 ;
;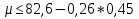 ;
;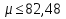 ;
;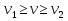
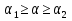
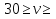 40
40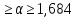
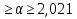
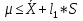 ;
;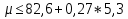 ;
;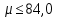 ;
;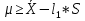 ;
;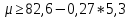 ;
;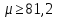 ;
;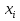
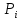
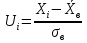
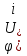
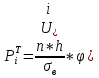
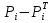
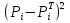
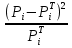
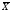 -R карту), по данным таблицы 1.2 (колонки Х1, Х2 и Х3, первые 30 значений). Выделить признаки действия особых причин (неуправляемого состояния процесса) по критериям ГОСТ Р 50779.42-99.
-R карту), по данным таблицы 1.2 (колонки Х1, Х2 и Х3, первые 30 значений). Выделить признаки действия особых причин (неуправляемого состояния процесса) по критериям ГОСТ Р 50779.42-99. 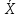
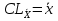
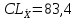
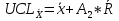
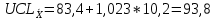
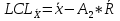
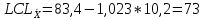
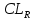
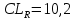
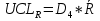
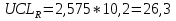
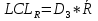
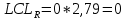
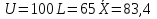
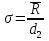 ;
; 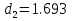 ;
;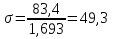 ;
;