Статистические методы регулирования технологических процессов
 Скачать 319.8 Kb. Скачать 319.8 Kb.
|
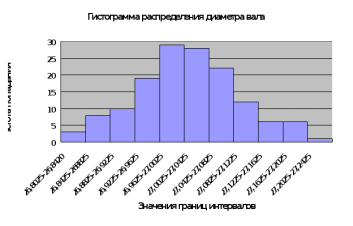 Рисунок 9. Анализ гистограммы. 1 Нашу гистограмму можно отнести к гистограмме обычного типа, что указывает на нормальный закон распределения случайной величины (закон Гаусса). 2. Параметры контролируемых деталей выходят за границы допуска распределения - это означает, что есть дефекты. 3. Настройка близка к нормальной, т.к. центр допуска и среднее значение очень близки по значению. 4.Воспроизводимость неудовлетворительная, т.к. допуск меньше рассеивания. 5.В нашем случае решением служит уменьшение разброса распределения. з) Строим график накопленных частот и определяем количество дефектов в процессе (Рисунок 6). е) Строим гистограмму накопленных частот (Рисунок 10). 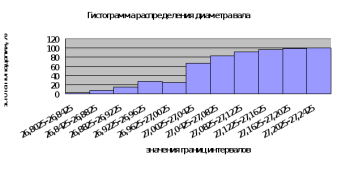  Рисунок 10. Анализ гистограмм. 1. Нашу гистограмму можно отнести к гистограмме обычного типа, что указывает на нормальный закон распределения случайной величины (закон Гаусса), 2. Есть дефекты, т. к. параметры контролируемых деталей выходят за границы допуска распределения. По графику накопительных частот определяем процент годных деталей 97%-7%=90%, соответственно процент дефектных деталей = 10 %. 3. Настройка близка к нормальной т.к. центр допуска и среднее значение очень близки по значению. 4.Воспроизводимость неудовлетворительная, т.к. допуск меньше рассеивания. 5.В нашем случае решением служит уменьшение разброса распределения. Вывод: в результате построения графика накопительных частот мы определили, что процент дефектных деталей составляет 10%. Резюме: в данном подразделе производился анализ процесса с использованием гистограмм в ходе которого определили, что тип гистограммы обычный, процент дефектных деталей равен 10%, настройка близка к нормальной, воспроизводимость неудовлетворительная. 3.3 УПРАВЛЕНИЕ ПРОЦЕССОМ ПО КОНТРОЛЬНЫМ КАРТАМ ШУХАРТА Задача: определить является ли процесс закономерным, стабильным и управляемым. Метод решения: построение х- S карт используя нормы Форда. Построение x – S карты первого дня, используя нормы Форда. Задача: определить является ли прочес закономерным, стабильным и управляемым; выходит ли размах за границы допуска. Основные параметры распределения занесены в таблицу (Таблица 6). Таблица 6.
Объём выборки n = 6. Количество выборок m = 8. Расчёт контрольных границ: UEGx, OEGx = x ± A3×s, где A3 = 1,287 (по табл.) OEGx = x + A3×s = 26,9917083333 + 1,287×0,09299964729= 27,1113988794 UEGx = x – A3×s = 26,9917083333 - 1,287×0,09299964729= 26,8720177872 OEGs = B4×s, где B4 = 1,97 (по табл.) OEGs = 1, 97×0,09299964729=0,18320930516 UEGs = B3×s, где B3 = 0,03 (по табл.) UEGs = 0, 03×0,09299964729=0,00278998941 Данные для построения x – S карты первого дня приведены в таблице (Таблица 7). Таблица 7.
Построение x – S карты первого дня (Приложение А). Вывод: Закономерности нет, процесс стабилен, управляем. Размах не выходит за границы процесса. Процесс можно продолжать. Построение x – S карты второго дня, используя нормы Форда. Задача: определить является ли прочес закономерным, стабильным и управляемым; выходит ли размах за границы допуска. При построении карт второго дня берём границы первого дня. Поэтому все расчёты совпадают с расчётами первого дня (Таблица 31). UEGx, OEGx = x ± A3×s, где A3 = 1,287 (по табл.) OEGx = x + A3×s = 26,9917083333 + 1,287×0,09299964729= 27,1113988794 UEGx = x – A3×s = 26,9917083333 - 1,287×0,09299964729= 26,8720177872 OEGs = B4×s, где B4 = 1,97 (по табл.) OEGs = 1, 97×0,09299964729=0,18320930516 UEGs = B3×s, где B3 = 0,03 (по табл.) UEGs = 0, 03×0,09299964729=0,00278998941 Данные для построения x – S карты второго дня приведены в таблице (Таблица 8). Таблица 8.
Построение x – S карты втторого дня (Приложение Б). Вывод: Закономерности нет, процесс стабилен, управляем. Размах не выходит за границы процесса. Процесс можно продолжать. Построение x – S карты третьего дня, используя нормы Форда. Задача: определить является ли прочес закономерным, стабильным и управляемым; выходит ли размах за границы допуска. При построении карт третьего дня берём границы второго дня. Поэтому все исходные данные для расчётов берём второго дня и заносим в таблицу (Таблица 9). Таблица 9.
Объём выборки n = 6. Количество выборок m = 8. Расчёт контрольных границ: UEGx, OEGx = x ± A3×s, где A3 = 1, 287 (по табл.) OEGx = x + A3×s = 27,036875+ 1, 283×0,10366324878= 27,1698749482 UEGx = x – A3×s = 27,036875- 1, 283×0,10366324878= 26,9038750518 OEGs = B4×s, где B4 = 1, 97 (по табл.) OEGs = 1, 97×0,10366324878=0,2042166 UEGs = B3×s, где B3 = 0, 03 (по табл.) UEGs = 0, 03 × 0,10366324878= 0,00310989746 Данные для построения x – S карты третьего дня приведены в таблице (Таблица 10). Таблица 10.
|
