Статистические методы регулирования технологических процессов
 Скачать 319.8 Kb. Скачать 319.8 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВПО «Уральский государственный экономический университет» Центр дистанционного образования Курсовая работа по дисциплине: Статистические методы в управлении качествомпо теме: Статистические методы регулирования технологических процессов Исполнитель: студент Губин М.В. Группа УК-13П Научный руководитель: Плиска О.В. г. Пермь 2014г. СОДЕРЖАНИЕ
ВВЕДЕНИЕ Любая продукция или услуга есть результат некоторого процесса. Под процессом подразумевают совокупность взаимосвязанных ресурсов и деятельности, которая преобразует входящие элементы в выходящие. Причем к ресурсам относятся персонал, оборудование, материалы, технология (методы и средства), окружающая среда, информация. По существу, процесс представляет собой взаимодействие людей, оборудования, материалов, методов и среды, в результате которого производится продукция или оказываются услуги. Все процессы и их результаты подвержены изменчивости – вариабельности. Поэтому при решении задач статистического управления процессами исходят из того, что как в производственных, так и в любых других процессах, всегда имеют место изменения или вариации, проявляющиеся в отклонении от целевых значений каких-либо параметров, характеризующих процесс. При естественном ходе процесса его изменчивость обычно обусловлена влиянием множества разнообразных случайных (обычных) неконтролируемых причин. Каждая из таких постоянно присущих причин составляет незначительную долю общей изменчивости, и ни одна из них не значима сама по себе. Тем не менее, сумма всех этих случайных причин изменчивости процесса измерима, и предполагается, что она внутренне присуща процессу. Исключение или уменьшение влияния обычных причин требует управленческих решений и выделения ресурсов на улучшение процесса и в ряде случаев оказывается экономически нецелесообразным или технически невозможным. Целью предложенной курсовой работы является практическое применение методов статистического регулирования технологических процессов на действующем серийном производстве. Задачи данной курсовой работы направлены на: закрепление теоретических знаний, полученных при изучении дисциплины; приобретение и закрепление навыков по практическому использованию статистических методов в управлении качеством; развитие навыков по обработке информации и принятию решений по управлению качеством на основе статистических законов. 1 СТАТИСТИЧЕСКОЕ РЕГУЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ. Статистическое регулирование технологических процессов – корректирование значений параметров технологического процесса по результатам выборочного контроля контролируемых параметров, осуществляемое для технологического обеспечения требуемого уровня качества. При этом технологический процесс должен быть статистически управляемым и стабильным . Принято считать, что процесс находится в “статистически управляемом состоянии” или “статистически управляем или контролируемым”, если источником его изменчивости являются только случайные (обычные) причины, которые имеют стабильное и повторяемое распределение во времени. Такую изменчивость процесса называют собственной. Любой процесс, находящийся в статистически управляемом состоянии, стабилен и характеризуется тем, что ход процесса предсказуем, его параметры со временем не отклоняются от целевых значений, а разброс параметров находится в прогнозируемых пределах. Однако естественный ход процесса может нарушаться из-за изменений, обусловленных неслучайными (особыми) причинами, внутренне не присущими процессу. Применительно к производственному процессу такими непредсказуемыми и нестабильными причинами могут быть поломка инструмента, неправильная настройка станка, его износ, недостаточная однородность обрабатываемого материала, нарушение рабочим требований документации из-за усталости или недомогания, ошибки контрольно-измерительного оборудования, колебания источников энергии, изменения окружающей среды и т.д. При воздействии на процесс неслучайных (особых) причин изменчивости он выходит из статистически управляемого состоянии, ход процесса становится непредсказуемым, его параметры могут существенно отклониться от целевых значений, разброс параметров может оказаться неприемлемым, а выход процесса нестабильным во времени. Когда процесс оказывается в “статистически неуправляемом состоянии”, необходимо возможно быстрее обнаружить неслучайные изменения процесса с тем, чтобы выявить их причину и своевременно внести необходимые корректировки в процесс. Тем самым предотвращаются существенные отклонения характеристик процесса от целевых значений, и обеспечивается поддержание процесса на приемлемом и стабильном уровне, гарантируя соответствие продукции и услуг установленным требованиям .[5, с.194-195] Статистическое регулирование технологических процессов заключается в том, что в определенные моменты времени или через определенное количество изготовленных единиц продукции отбирается мгновенная выборка установленного объема и производится измерение контролируемого параметра. По результатам измерений определяют статистическую характеристику контролируемого параметра, значение которой наносят на контрольную карту и, в зависимости от этого значения принимают решение о корректировке технологического процесса или о продолжении процесса баз корректировки, т.е. на основании данных о состоянии технологического процесса в предшествующие моменты времени прогнозируется его состояние в последующие моменты времени. Значение статистической характеристики контролируемого параметра качества продукции, при котором наступает разладка операции или процесса, должно определяться, исходя из выборочной характеристики .[6, с.99] 1.1 ОБЛАСТИ ПРИМЕНЕНИЯ СТАТИСТИЧЕСКОГО КОНТРОЛЯ Статистические методы контроля используют в машиностроении - химической, металлообрабатывающей, сталелитейной, электротехнической, радиотехнической, нефтяной промышленности, приборостроении, производстве красителей и пластических материалов, в производстве упаковочных материалов, оптических приборов и т. д., а так же в сферах лёгкой промышленности (пищевой, аптекарской, текстильной, обувной) и в области коммунальных услуг (в сфере гостиниц, транспорта, телефонной связи). [8, с.18] Роль статистических методов контроля высоко ценится многими специалистами. Статистические методы обеспечивают повышение качества выпускаемой продукции, повышение надёжности и снижение расходов на качество. 1.2 ПЯТЬ СЕКРЕТОВ ЭФФЕКТИВНОСТИ МЕТОДОВ СТАТИСТИЧЕСКОГО КОНТРОЛЯ 1. Статистический контроль качества (СКК) – это переход от тейлоровских механизмов управления качеством отдельных изделий к механизмам управления качеством совокупностей изделий, продукции (партий, протоколов). 2. СКК – это технология сбора, компактного хранения и научно обоснованной обработки информации о качестве продукции. 3. СКК – это экономия затрат на контроль в результате перехода от сплошного к выборочному контролю. 4. СКК – это информационная основа правовых производственных отношений между изготовителями и потребителями при оптовых поставках, при аттестации производств и технологических процессов, при сертификации продукции, при надзоре контролирующих государственных органов за соблюдением обязательных требований стандартов. 5. СКК – это повышенная ответственность и гарантии изготовителей. Правильное применение статистических методов контроля даёт потребителю гарантии, что дефектность продукции в партиях будет не выше установленных заранее величин. .[20, с.87] При внутризаводском применении статистический контроль повышает ответственность контролёров и исполнителей. При сплошном контроле, приняв продукцию, контролёры далее уже сами отвечают перед исполнителями следующих операций. Это порождает определённую психологию у рабочих – любой ценой «протолкнуть » продукцию через контролёров. При статистическом контроле участок и после контроля несёт ответственность и за каждое изделие, и за партию в целом. При этом на рабочие участке начинают следить за дефектностью продукции и стремятся её уменьшить. 1.3 ВИДЫ СТАТИСТИЧЕСКОГО РЕГУЛИРОВАНИЯ ТЕХНОЛОГИСЕСКИХ ПРОЦЕССОВ Задача статистического регулирования технологического процесса состоит в том, чтобы на основании результатов периодического контроля выборок малого объема приходить к заключению: "процесс налажен" или "процесс разлажен". Выявление разладки технологического процесса основано на результатах периодического контроля малых выборок, осуществляемого по количественному или альтернативному признакам. Для каждого из этих способов контроля используются свои статистические методы регулирования. Контроль по количественному признаку заключается в определении с требуемой точностью фактических значений контролируемого параметра у единиц продукции из выборки. Фактические значения контролируемого параметра необходимы для последующего вычисления статистических характеристик, по которым принимается решение о состоянии технологического процесса. Такими характеристиками являются медиана и выборочное среднее; квадратическое отклонение и размах. Первые две характеристики – характеристики положения, а последние две – характеристики рассеивания случайной величины Х. .[4, с.65-66] Контроль по альтернативному признаку заключается в определении соответствия контролируемого параметра или единицы продукции установленным требованиям. При этом каждое отдельное несоответствие установленным требованиям считается дефектом, а единица продукции, имеющая хотя бы один дефект, считается дефектной. При контроле по альтернативному признаку не требуется знать фактическое значение контролируемого параметра – достаточно установить факт соответствия или несоответствия его установленным требованиям. Поэтому можно использовать простейшие средства контроля: шаблоны, калибры, контроль по образцу и др. Решение о состоянии технологического процесса принимается в зависимости от числа дефектов или числа дефектных единиц продукции, обнаруженных в выборке. Каждый из перечисленных способов контроля имеет свои преимущества и свои недостатки. Преимущество контроля по количественному признаку состоит в том, что он более информативен (по сравнению с контролем по альтернативному признаку) и поэтому требует меньшего объема выборки. Однако такой контроль более дорогой, поскольку для него необходимы такие технические средства контроля, которые позволяют получать фактические значения контролируемого параметра. Кроме того, для статистического регулирования при контроле по количественному признаку необходимы вычисления, связанные с определением статистических характеристик. [13, с.93] Преимущество контроля по альтернативному признаку заключается в его простоте и относительной дешевизне, поскольку можно использовать простейшие средства контроля или визуальный контроль. К недостаткам такого контроля относится его меньшая информативность, что требует значительно большего объема выборки при равных исходных данных . 2. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАТИСТИЧЕСКОГО РЕГУЛИРОВАНИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ. 2.1 КОНТРОЛЬ ПО КОЛИЧЕСТВЕННОМУ ПРИЗНАКУ. Любой контролируемый параметр по своей природе является случайной величиной, поскольку он может принять то или иное значение, причем заранее неизвестное. Изучением случайных величин занимается теория вероятностей. Эта математическая наука позволяет получать вполне определенные количественные результаты и на их основе принимать достаточно обоснованные и в основном правильные решения. Все случайные величины подчиняются определенным закономерностям, называемым законами распределения. Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Сумма вероятностей всех возможных значений случайной величины равна единице. Эта суммарная вероятность каким-то образом распределена между отдельными значениями, что полностью определяется законом распределения. Законы распределения могут быть представлены в аналитической, табличной или графической формах. Законы распределения имеют большое прикладное значение в различных областях человеческой деятельности и, в частности, в области промышленного производства для решения задач, связанных с обеспечением качества продукции. Случайные величины могут быть либо дискретными, либо непрерывными, которые описываются различными законами распределения. Дискретными называются такие случайные величины, которые можно заранее перечислить. Например, число дефектных единиц продукции или число дефектов. Непрерывными называются случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток. Примером непрерывной случайной величины является любая измеряемая величина, например, размер детали. В теории вероятностей рассматривается достаточно большое количество разнообразных законов распределения. Для решения задач, связанных с построением контрольных карт, представляют интерес лишь некоторые ив них. Важнейшим из них является нормальный закон распределения, который применяется для построения контрольных карт, используемых при контроле по количественному признаку, т.е. когда мы имеем дело с непрерывной случайной величиной. Нормальный закон распределения занимает среди других законов распределения особое положение. Это объясняется тем, что, во-первых, наиболее часто встречается на практике, и, во-вторых, он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Что касается второго обстоятельства, то в теории вероятностей доказано, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, могут быть представлены как сумма весьма большего числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием отдельной причины, независящей от остальных. В графической форме нормальный закон распределения изображается колоколообразной кривой (рисунок1). 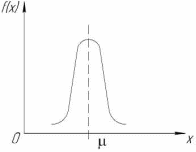 Рисунок 1 - Кривая нормального законно распределения Этой кривой определяется плотность вероятности f(х) значений случайной величины 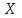 . .Форма этой кривой определяется выражением: 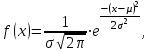 (1.1) (1.1) где 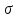 – среднее квадратичное отклонение случайной величины – среднее квадратичное отклонение случайной величины 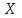 ; ; 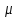 – математическое ожидание случайной величины – математическое ожидание случайной величины 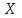 ; ; 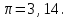 Максимальная ордината кривой равна 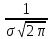 при при 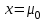 . (1.2) [10, с.121] . (1.2) [10, с.121]По мере удаления от точки 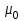 плотность распределения уменьшается, и при плотность распределения уменьшается, и при 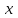 стремящимся к бесконечности кривая асимптотически приближается к оси абсцисс. стремящимся к бесконечности кривая асимптотически приближается к оси абсцисс.Кривая нормального распределения характеризуется двумя параметрами: 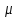 и и 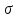 . Смысл этих параметров состоит в следующем. Значением определяется центр рассеивания – если изменять центр рассеивания, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рисунок 2). Таким образом, значением . Смысл этих параметров состоит в следующем. Значением определяется центр рассеивания – если изменять центр рассеивания, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рисунок 2). Таким образом, значением 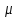 определяется положением кривой распределения на оси абсцисс. Размерность определяется положением кривой распределения на оси абсцисс. Размерность 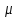 такая же, что и размерность случайной величины такая же, что и размерность случайной величины 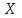 . .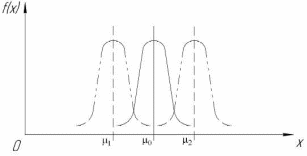 Рисунок 2. - Кривые распределения нормального распределения при изменении центра рассеивания Значением 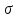 определяется форма кривой распределения. определяется форма кривой распределения. Поскольку площадь под кривой распределения должна всегда оставаться равной единице, то при увеличении 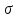 кривая распределения становится более плоской. На рисунке 3 показаны три кривые при разных кривая распределения становится более плоской. На рисунке 3 показаны три кривые при разных 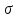 : : 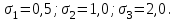  Рисунок 3. Кривые распределения при разных значениях 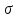 статистический метод управление качество Таким образом, значением 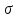 определяется форма кривой распределения –это есть характеристика рассеивания. Размерность параметра определяется форма кривой распределения –это есть характеристика рассеивания. Размерность параметра 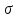 совпадает с размерностью случайной величины совпадает с размерностью случайной величины 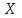 . .Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины  , подчиненной нормальному закону с параметрами м, у, на участок от А до В. Таким участком может быть, например, поле допуска от верхнего значения , подчиненной нормальному закону с параметрами м, у, на участок от А до В. Таким участком может быть, например, поле допуска от верхнего значения 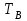 до нижнего – до нижнего – 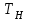 . .Эту задачу решают по формуле 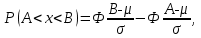 (1.3) [10, с.121] (1.3) [10, с.121]где 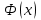 – есть нормальная функция распределения с параметрами – есть нормальная функция распределения с параметрами 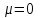 и и 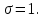 Значения 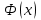 определяют по таблице . определяют по таблице .Для отрицательных значений 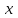 функцию определяют из соотношения функцию определяют из соотношения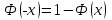 . (1.4) . (1.4)Это соотношение следует из симметричности нормального распределения относительно начала координат. По формуле 1.3. можно определись вероятность попадания контролируемого (по количественному признаку) параметра в поле допуска, ограниченного значениями 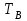 , ,  . Заменив в формуле 1.3. значения А и В на . Заменив в формуле 1.3. значения А и В на  и и 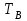 соответственно, получим формулу для решения нашей задачи: соответственно, получим формулу для решения нашей задачи: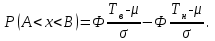 (1.5) [10, с.122] (1.5) [10, с.122]По сути этой вероятностью определяется вероятная доля годной продукции (по контролируемому параметру). Если из единицы вычесть вероятную долю годной продукции, то получим вероятную долю дефектной продукции, которую обозначим через 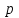 : :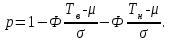 (1.6) (1.6)Граница регулирования для контрольных карт средних арифметических значений определяют также с помощью закона нормального распределения. В качестве случайной величины используют значение 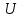 : :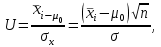 (1.7) (1.7)где 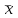 – выборочное среднее арифметическое значение случайной величины – выборочное среднее арифметическое значение случайной величины 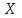 ; ; 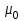 – математическое ожидание случайной величины – математическое ожидание случайной величины 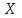 при налаженном состоянии технологического процесса (обычно за при налаженном состоянии технологического процесса (обычно за 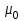 принимают середину поля допуска); принимают середину поля допуска); 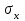 – среднее квадратическое отклонение выборочного среднего ( – среднее квадратическое отклонение выборочного среднего (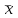 ), которое связано со средним квадратическим отклонением случайной величины соотношением ), которое связано со средним квадратическим отклонением случайной величины соотношением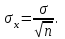 (1.8) (1.8)Случайная величина 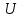 , как и случайная величина , как и случайная величина 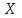 , распределена нормально, причем ее математическое ожидание равно нулю, а среднее квадратическое отклонение , распределена нормально, причем ее математическое ожидание равно нулю, а среднее квадратическое отклонение 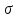 равно единице. равно единице.Поэтому, для решения задачи статистического регулирования можно использовать таблицу функции нормированного нормального распределения. Тогда условием налаженности технологического процесса является выполнение неравенства: 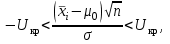 (1.9) (1.9)где 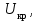 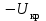 – критические значения, которые для статистического регулирования обычно устанавливают равными +3, -3. Отсюда получаем: – критические значения, которые для статистического регулирования обычно устанавливают равными +3, -3. Отсюда получаем: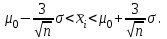 (1.10) [10, с.123] (1.10) [10, с.123]Таким образом, процесс будет признаваться налаженным до тех пор, пока выборочное среднее арифметическое 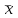 не превысит значение в левой или правой частях этого неравенства, которыми определяется положение границ регулирования на контрольной карте средних арифметических значений. Обозначим их не превысит значение в левой или правой частях этого неравенства, которыми определяется положение границ регулирования на контрольной карте средних арифметических значений. Обозначим их 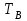 – для верхней границы регулирования и – для верхней границы регулирования и 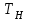 – для нижней границы регулирования . [7, с.18] – для нижней границы регулирования . [7, с.18]2.2 КОНТРОЛЬ ПО АЛЬТЕРНАТИВНОМУ ПРИЗНАКУ. При контроле по альтернативному признаку мы имеем дело с дискретными случайными величинами – это число дефектных единиц продукции или число дефектов. При статистическом регулировании возникает задача выбора критерия для оценки состояния технологического процесса. Здесь могут быть разные подходы. Рассмотрим один из них, на основе которого строятся контрольные карты. По периодически отбираемым выборкам объема 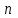 требуется оценить состояние технологического процесса – процесс налажен или он разлажен. требуется оценить состояние технологического процесса – процесс налажен или он разлажен. Оценка проводиться на основе подсчета числа дефектных единиц продукции или числа дефектов в выборке. Необходимо определить, какое число считается допустимым. Видимо это число должно быть таким, при котором хорошие партии будут приниматься с большой вероятностью, что и будет свидетельствовать о налаженном состоянии технологического процесса. Эту вероятность вычисляют по известной в теории вероятностей формуле, которую называют функцией гипергеометрического распределения: 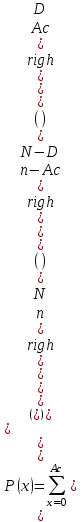 (1.11) (1.11)где 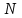 – объем партии, определяемый как количество изделий изготовляемых за время – объем партии, определяемый как количество изделий изготовляемых за время 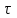 ; ; 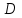 – допустимое количество дефектных изделий или допустимое число дефектов в партии объема – допустимое количество дефектных изделий или допустимое число дефектов в партии объема 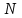 , определяемое значением AQL; , определяемое значением AQL; 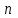 – объем выборки; – объем выборки; 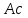 – допустимое количество дефектных изделий или допустимое число дефектов в выборке объема – допустимое количество дефектных изделий или допустимое число дефектов в выборке объема 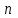 . .Выражение в скобках в формуле 1.11. и есть биноминальные коэффициенты, например, 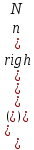 (1.12) (1.12)где 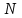 – объем партии, определяемый как количество изделий изготовляемых за время – объем партии, определяемый как количество изделий изготовляемых за время 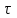 ; ; 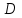 – допустимое количество дефектных изделий или допустимое число дефектов в партии объема – допустимое количество дефектных изделий или допустимое число дефектов в партии объема 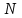 , определяемое значением AQL; , определяемое значением AQL; 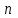 – объем выборки; – объем выборки; 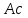 – допустимое количество дефектных изделий или допустимое число дефектов в выборке объема – допустимое количество дефектных изделий или допустимое число дефектов в выборке объема 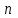 . [15] . [15]2.3 КОНТРОЛЬНЫЕ КАРТЫ. Контрольные карты являются основным инструментом статистического управления качеством. Контрольные карты применяют для сравнения получаемой по выборкам информации о текущем состоянии процесса с контрольными границами, представляющими пределы собственной изменчивости (разброса) процесса. [2, с.16] Собственный разброс характерен для всех процессов из-за большого числа незначительных случайных воздействий. Вследствие этого результаты измерений, полученные в ходе нормального течения процесса, непостоянны. Непостоянны и отслеживаемые статистические характеристики, например выборочное среднее, медиана и т.п. Поэтому необходимо ввести статистически обоснованные границы для данной отслеживаемой характеристики с целью минимизировать ошибочные решения при управлении процессом . Цель контрольных карт – обнаружить неестественные изменения в данных из повторяющихся процессов и дать критерии для обнаружения отсутствия статистической управляемости . Контрольная карта – это карта, на которой для наглядности отображения состояния процесса отмечают значения соответствующей выборочной характеристики смежных выборок во временной последовательности. В качестве выборочной характеристики могут использоваться индивидуальные значения какого-либо параметра продукции, среднее арифметическое значение, медиана, среднее квадратическое (стандартное) отклонение, размах, доля или число несоответствующих единиц продукции, число несоответствий и др. По существу, контрольная карта представляет собой графическое отображение состояния процесса, его уровня и изменчивости. [9, с.266-267] Контрольные карты строят в произвольном масштабе на листе бумаги или экране дисплея компьютера. По оси абсцисс откладывают моменты взятия выборок или их текущие номера, а по оси ординат – реализации выборочной характеристики. Для наглядности точки значений выборочной характеристики, соответствующее двум последовательным выборкам, соединяют отрезками прямых линий и получают линейный график, показывающий динамику поведения процесса. В качества ориентира на контрольной карте проводится центральная линия (ЦЛ) – прямая, параллельная оси абсцисс и определяющая среднее процесса. Ее расстояние от оси абсцисс соответствует заданному в нормативной или технической документации номинальному значению контролируемого параметра, например, центру поля допуска, математическому ожиданию значений выборочной характеристики, или же оценочному значению, прогнозируемому по результатам изучения предыстории процесса. Параллельно ЦЛ на контрольной карте наносятся две линии – верхняя (ВКГ) и нижняя (НКГ) контрольные границы, называемые иногда границами регулирования. По существу, контрольные границы, указывающие момент разладки процесса, ограничивают диапазон неизбежного разброса значений выборочной характеристики, т.е. разброса, обусловленного неустранимыми в настоящее время обычными причинами, и позволяют судить, находится ли процесс в статистически управляемом состоянии или он подвергнут влиянию особых причин. Кроме того, на контрольную карту в ряде случаев наносятся еще две дополнительные линии – верхняя (ВПГ) и нижняя (НВГ) предупреждающие границы, которые располагаются ближе друг к другу, чем ВКГ и НКГ. Если значениям выборочной характеристики присуще одностороннее отклонение от ЦЛ, то используют контрольные карты с односторонними (верхними или нижними) границами . Пример контрольной карты представлен на рисунке 4. 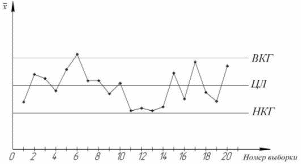 Рисунок 4 - Контрольная карта средних арифметических значений На контрольной карте показаны средние арифметические значения ( 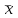 ) для 20 последовательных выборок по 5 изделий каждая. Выборки берутся примерно через один час. Большинство точек на карте расположены около средней линии и находятся между двумя пунктирными линиями, ) для 20 последовательных выборок по 5 изделий каждая. Выборки берутся примерно через один час. Большинство точек на карте расположены около средней линии и находятся между двумя пунктирными линиями, которые называются контрольными пределами. Сигналом о возможной разладке технологического процесса могут служить: — выход точки за контрольные пределы (выборка №6); — расположение группы последовательных точек около одной контрольной границы, но не выход за нее (выборка №11-14), что свидетельствует о нарушении уровня настройки оборудования; — сильное рассеяние точек на контрольной карте относительно средней линии (выборки №15-20), что свидетельствует о снижении точности технологического процесса. При наличии сигнала о нарушении производственного процесса должна быть выявлена и устранена причина нарушения. Ввиду того что границы статистического регулирования (контрольные пределы) определяются статистическими методами, то возможны ошибки двух видов: поступает сигнал о нарушении технологического процесса, в то время как в действительности нарушение отсутствует (ошибка первого рода); сигнал о нарушении технологического процесса не поступает, в то время как нарушение имеет место (ошибка второго рода). Очевидно, на практике эти ошибки должны встречаться достаточно редко. Поэтому контрольные пределы стараются выбирать таким образом, чтобы минимизировать вероятности появления ошибок как первого, так и второго рода. Эти требования противоречивые, и уменьшение вероятности одной ошибки ведет к увеличению вероятности другой . Преимущество контрольно карты – простота ее построения и применения. Она служит своевременным индикатором статистически управляемого процесса. Однако контрольная карта – только часть полной системы анализа процесса. С ее помощью можно предсказать момент, когда определенная причина изменит течение процесса, но для установления ее природы и корректировки процесса необходимо проводить независимое исследование. [17, с.22] 3 ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ КОНТРОЛЯ НА ОАО «ПМЗ». 3.1 ОБЩИЕ СВЕДЕНИЯ О ПРЕДПРИЯТИИ В 1930 году принято решение Совета Труда и Обороны СССР о строительстве в г. Пермь моторостроительного завода «М» (в последствии, завод назван именем И.В. Сталина и ему присвоен №19). Директором строительства назначен П.И. Чубуков. Техническим директором и Главным конструктором будущего завода назначен Аркадий Дмитриевич Швецов (в 1927 году А.Д. Швецов создал первый отечественный авиационный мотор М-11, установленный на легендарный самолет-биплан У-2 (По-2) конструкции Н.Н. Поликарпова). С 1930 по 1932 год ведется строительство вспомогательных помещений и производств. К строительству самого завода приступили в 1932 году. Производственные мощности завода были рассчитаны на выпуск 600 моторов в год. Изначально, завод №19 ориентирован на выпуск моторов воздушного охлаждения. Завод был запущен в 1934 году и в 1934 конструкторские подразделения завода №19 выделены в опытно-конструкторский отдел. Директором завода назначен И.И. Побережский. В 1939 году, под руководством Швецова, для самолетов И-16 и И-153 создается новый мотор М-63 (1100 л.с.). В том же году принято Постановление Правительства №2032-569 об образовании Опытно-конструкторского бюро №19 (ОКБ-19) как самостоятельного предприятия (в 1966 году ОКБ-19 переименовано в МКБ, в 1989 году МКБ переименовано в НПО «Авиадвигатель», а в 1992 на базе НПО «Авиадвигатель» создано акционерное общество). В 1942 году завод возглавил А.Г. Солдатов. Его имя в настоящее время носит Муниципальный Дворец Культуры и одна из улиц Перми. В 1943 году, под руководством Швецова, создан мотор М-82ФН (1850 л.с.) для истребителей Ла-5ФН и Ла-7 и для бомбардировщика Ту-2. Этот мотор представляет собой форсированный, с непосредственным впрыском топлива, вариант мотора М-82. К 1948 году, на заводе №19 освоено серийное изготовление двигателя АШ-73ТК для стратегического бомбардировщика Ту-4. Для увеличения высотности работы, этот мотор оснащен двумя турбокомпрессорами ТК-19. С 1952 года пермский завод №19 им. Сталина серийно выпускает вертолетные моторы АШ-82В, созданные коллективом ОКБ-19 на основе мотора М-82ФН и предназначенные для установки на вертолеты Ми-4 и Як-24. На вертолете Ми-24 установлен мировой рекорд высоты, на Як-24 – грузоподъемности. С 1955 по 1957 завод выпускает реактивные двигатели АМ-3 конструктора А.Д. Микулина для бомбардировщика Ту-16. С 1957 по 1959 завод изготавливает двигатели РД-3М для первого в мире реактивного пассажирского лайнера Ту-104. С 1958 года завод выпускает турбовинтовой двигатель АИ-20 который устанавливается на пассажирский самолет Ил-18 и транспортные самолеты Ан-10 и Ан-12. С 1958 года завод выпускает двигатель Д-20П конструктора П.А. Соловьева тягой 5400 кгс. Двигатель устанавливался на пассажирский самолет Ту-124. С 1959 года завод выпускает вертолетные турбовальные двигатели Д-25В конструктора П.А. Соловьева. Этот двигатель устанавливался на вертолеты Ми-6, Ми-10 и Ми-10К. Модификация двигателя Д-25В устанавливалась на вертолет-винтокрыл Ми-12. С 1966 года пермский завод, переименованный к тому времени в завод им. Я.М. Свердлова, выпускает двухконтурный турбореактивный двигатель Д-30 тягой 6800 кгс конструкции П.А. Соловьева для самолета Ту-134 31 декабря 1970 года завод им. Свердлова награжден орденом Ленина. В 1979 году Соловьевым создан двухконтурный турбореактивный двигатель Д-30Ф6 с форсажной камерой (тяга без форсажа 9500 кгс, на форсаже 15500 кгс). Д-30Ф6 устанавливается на перехватчик МиГ-31. Двигатель не имеет аналогов в мире. А самолет МиГ-31 представляет собой уникальный, не имеющий себе равных, обладающий современным радиоэлектронным оборудованием и вооружением, комплекс. В 1979 году завод им. Свердлова преобразован в Пермское Производственное Объединение «Моторостроитель» им. Свердлова. В 1984 году ППО «Моторостроитель» им. Свердлова начинает выпуск двигателя Д-30КУ-154 (тягой 11000 кгс) конструктора Соловьева для самолета Ту-15423 мая 1984 года ППО «Моторостроитель» им. Свердлова награждено орденом Ленина. В 1988 году ППО «Моторостроитель» начинает выпуск двигателя ПС-90А (тягой 16000 кгс) конструкции Соловьева. Это первый в России двигатель получивший сертификат типа. Двигатель устанавливается на коммерческие самолеты Ил-96-300, Ту-204, Ту-214. Двигатели ПС-90А установлены на самолет Ил-96 Президента России. В 90-е годы предприятия раздробилось на ряд акционерных обществ по специфике производств (кроме авиационных двигателей завод выпускал и продолжает выпускать вертолетные редукторы, ракетные двигатели, мотоблоки). Так появились АО «Редуктор», АО «Протон», АО «Металлист» и др. Однако, самым крупным остается ОАО «Пермский Моторный Завод», В настоящее время ОАО «Пермский Моторный Завод» изготавливает и ремонтирует авиационные двигатели Д-30 и ПС-90А, а так же изготавливает и ремонтирует наземные ГТУ различной мощности. 15.04.2008 года Советом директоров ОАО «ПМЗ» была разработана и внедрена система менеджмента качества, действующая почти четыре года с момента издания. Контроль и внесение изменений в руководство предписаны подразделению по управлению документацией. Технологические процессы организованные на предприятии включают в себя весь спектр самых разнообразных процессов, необходимых для производства двигателей – от заготовительных (штамповка, поковка, литьё и т.д.) до сборочных и испытательных. 3.2 ИСПОЛЬЗОВАНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ КОНТРОЛЯ На предприятии статистические методы контроля используют различные службы, например, представитель заказчика. Он проводит контроль для того, чтобы воздействовать на нас (производителей), а так же защитить производство от партий, засоренных большим количеством дефектных изделий. В основном такой контроль происходит при сборке двигателей специального назначения (т.е. на самолёты для президента и его команды). При таком контроле от каждой партии деталей произвольно выбирают несколько деталей. Представитель заказчика лично меряет некоторые размеры на своё усмотрение. По результатам этих обмеров заказчик сам принимает решение о соответствии всей партии деталей установленным требованиям и решает можно ли отправлять эту партию на сборку. Кроме этого выборочный контроль используется на нашем предприятии для контроля работы отделов технического контроля. При этом один раз в год делается выборка из партии деталей уже проверенных контролёром ОТК. Её отправляют для измерения в центральную измерительную лабораторию (ЦИЛ). Как правило, выбирают наиболее сложные и ответственные детали, с точными размерами и посадочными диаметрами. По результатам измерения делается заключение, соответствует ли партия установленным требованиям и делают вывод относительно приёмки партии продукции контролёром, проверявшим эти детали в цехе. Ещё статистические методы контроля на нашем предприятии применяют для своевременного обнаружения разлада технологического процесса и для обеспечения качества продукции в процессе её производства. Технологический процесс состоит из ряда технологических операций. На некоторые из них вводят контрольные операции (межоперационный контроль) с целью предупреждения появления дефектной продукции. Здесь сплошной контроль заменён статистическим регулированием технологических процессов. По результатам контроля выборки небольшого объёма делают выводы о качестве продукции в процессе её производства. Постановка задачи. На машиностроительном предприятии происходит процесс изготовления детали вал. В течение трёх дней через каждый час (3 × 8) необходимо брать выборку по одной детали с каждого из 6 рабочих мест (объёмом 6 деталей). В результате у нас получились результаты контроля выборок в виде 144 количественных значений. В течение всего процесса измерения обеспечивалось поддержание нормальных условий в рабочем пространстве. Выдержаны нормальные значения основных влияющих величин: температура окружающей среды, относительная влажность окружающего воздуха и скорость движения воздуха. В работе мы даём оценку нашему техпроцессу на основе методики управления Деминга. Анализируя данные процесса, мы должны выяснить использовать данный процесс или необходимо остановить его и улучшить. Основная часть. 1. Организация сбора данных. Для выполнения сбора данных необходимо выполнить следующие этапы: Разработка контрольного листка (бланка). Сбор данных. Для этого необходимо измерить и зафиксировать в контрольном листе диаметр 27±0,15 деталей изготовленных на шести станках в течение восьмичасовой рабочей смены. Замеры велись 3 дня.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
