СТАТИСТИКА (ответы). Статистика общественная наука, исследующая количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной. Предмет статистики
 Скачать 281.01 Kb. Скачать 281.01 Kb.
|
|
Относительная величина структуры (ОВС) характеризует структуру совокупности, определяет долю (удельный вес) части в общем объеме совокупности. ОВС рассчитывают как отношение объема части совокупности к абсолютной величине всей совокупности, определяя тем самым удельный вес части в общем объеме совокупности (%): Относительная величина координации (ОВК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнения (%): Относительная величина планового задания (ОВПЗ) используется для расчета в процентном отношении увеличения (уменьшения) величины показателя плана по сравнению с его базовым уровнем в предшествующем периоде, для чего используется формула Относительная величина уровня выполнения плана (ОВУВП) характеризует степень выполнения планового задания за отчетный период (%) и рассчитывается по формуле 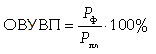 где Рф - величина выполнения плана за отчетный период; Рпл - величина плана за отчетный период. где Рф - величина выполнения плана за отчетный период; Рпл - величина плана за отчетный период.Относительная величина динамики (ОВД) характеризует изменение объема одного и того же явления во времени в зависимости от принятого базового уровня. ОВД рассчитывают как отношение уровня анализируемого явления или процесса в текущий момент времени к уровню этого явления или процесса за прошедший период времени. При исчислении этой величины в процентах получаем темп роста. Темпы роста можно просчитывать как с постоянным базовым уровнем (базисные темпы роста - ОВДб ), так и с переменным базовым уровнем (цепные темпы роста - ОВДц ): Относительная величина сравнения (ОВСр) - соотношение одноименных абсолютных показателей, относящихся к разным объектам, но к одному и тому же времени: Относительные величины интенсивности (ОВИ) применяются при исследовании степени объемности явления по отношению к объему среды, в которой происходит распространение этого явления. ОВИ здесь показывает, сколько единиц одной совокупности (числитель) приходится на одну, на десять, на сто единиц другой совокупности (знаменатель). ОВИ рассчитывается по формуле Билет №11. Средняя величина как обобщающая характеристика совокупности. Научные принципы расчета средних величин. Средняя величина – обобщающая характеристика качественно однородной совокупности однотипных явлений по какому-то одному качественно варьирующемуся признаку. Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы. Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Характеристики:
На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой. Расчет средней величины включает две операции: суммирование данных по всем единицам (обобщение данных) и деление на число единиц (приведение обобщенной характеристики к единице совокупности). Используются две категории средних величин: степенные средние; структурные средние. Первая категория степенных средних включает: среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую. Вторая категория (структурные средние) - это мода и медиана. Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Билет №12. Средняя арифметическая: простая и взвешенная; особенности применения. Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности. Формула средней арифметической (простой) имеет вид 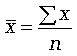 где n - численность совокупности. где n - численность совокупности.При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид 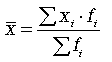 Можно выделить три основных свойства: 1) Свойство первое (нулевое): сумма отклонений индивидуальных значений признака от его среднего значения равна 0; 2) Свойство второе (минимальное): сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа (а), т.е. есть число минимальное; 3) Свойство третье: средняя арифметическая постоянной величины равна этой постоянной: Кроме этих трех важнейших свойств средней арифметической существуют расчетные свойства: 4) если индивидуальное значение признака каждой единицы умножить или разделить на постоянное число, то средняя арифметическая увеличится или уменьшится во столько же раз; 5) средняя арифметическая не изменится, если вес (частоту) каждого значения признака разделить на постоянное число; 6) если индивидуальные значения признака каждой единицы уменьшить или увеличить на одну и ту же величину, то средняя арифметическая уменьшится или увеличится на ту же самую величину. Билет №13. Средняя гармоническая: простая и взвешенная; особенности применения В средней гармонической, в отличии от средней арифметической, весами являются не прямые частоты признака, а их произведение на величину признака. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы: 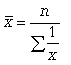 К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость: 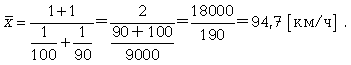 В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид 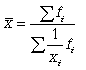 Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель. Билет №14. Показатели отклонений от средней величины: методика расчета и особенности применения. Для того, чтобы судить о типичности средней для данной совокупности, ее следует дополнить показателями, характеризующими вариацию величины изучаемого признака. Для измерения степени вариации единиц совокупности по изучаемому признаку используют абсолютные и относительные показатели вариации. Абсолютные: 1) Размах вариации (R) =хmax-хmin 2) Среднее линейное отклонение (d) = (∑|xi-xср|)/n (для сгруппированных (∑|xi-xср|*fi)/∑fi 3) Дисперсия (σ2) = (∑(xi-xср)2)/n (для сгруппированных (∑(xi-xср)2*fi)/∑fi 4) Среднее квадратическое отклонение (σ) = корень из дисперсии Относительные: 1) Относительный размах вариации (KR) = (R/хср)*100(%) 2) Относительное линейное отклонение (Kd) = (d/хср)*100(%) 3) Коэффициент вариации (υ) = (σ/хср)*100(%) При нормальном распределении в пределах хср+- σ располагается 0,683 кол-ва наблюдений, в пределах хср+- 2σ располагается 0,954, в пределах хср+- 3σ располагается 0,997 (максимально возможное отклонение). Билет №15. Виды динамических рядов и правила их построения. Ряд динамики – ряд показателей, характеризующий изменение изучаемых явлений во времени. Каждый динамический ряд содержит две составляющие: 1) показатели периодов времени (“t” - годы, кварталы, месяцы, дни или даты); 2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда (“y”). Уровни ряда выражаются как абсолютными, так и средними или относительными величинами. В зависимости от характера показателей строят динамические ряды абсолютных, относительных и средних величин. Ряды динамики из относительных и средних величин строят на основе производных рядов абсолютных величин. Различают интервальные и моментные ряды динамики. Динамический интервальный ряд содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объем явления за более длительный период, или так называемые накопленные итоги. Динамический моментный ряд отражает значения показателей на определенный момент времени (дату времени). В моментных рядах исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. Накопленные итоги здесь не рассчитываются. Моментные ряды делятся на ряды с равными промежутками времени и с неравными промежутками времени. Правила построения динамического ряда: 1) Все показатели одного динамического ряда должны относиться к равнозначным периодам времени; 2) Показатели динамического ряда должны быть однородны по состав, т.е. иметь одну и ту же полноту охвата объектов наблюдения; 3) Показатели должны быть рассчитаны по одной методологии; 4) При построении динамического ряда должна соблюдаться последовательности и непрерывность ряда (при разрыве – интерполяция + экстраполяция). Для того чтобы избежать искажения реальной динамики, в статистическом исследовании проводятся предварительные расчеты (смыкание рядов динамики), которые предшествуют статистическому анализу динамических рядов. Под смыканием рядов динамики понимается объединение в один ряд двух и более рядов, уровни которых рассчитаны по разной методологии или не соответствуют территориальным границам. Смыкание рядов динамики может предполагать также приведение абсолютных уровней рядов динамики к общему основанию. Билет №16. Средняя хронологическая: ее значение, методики расчета. Исходным, при построении любого динамического ряда, является уровень динамики, но для общей характеристики за весь охватываемый период рассчитывают средний уровень ряда, т.е. среднюю величину из всех совокупностей ряда. В рядах динамики средняя из уровней называется хронологической средней. Средний уровень дает общее представление и развитие явления не за определенные моменты, а за весь процесс. В интервальных рядах средний уровень рассчитывается по формуле средней арифметической простой: В моментных рядах динамики с равными промежутками времени между моментами: В моментных рядах с неравностоящими друг от друга уровнями: Билет №17. Производные абсолютные показатели динамического ряда. Анализ скорости и интенсивности развития явления во времени осуществляется с помощью аналитических показателей, которые получаются в результате сравнения уровней ряда динамики между собой. К таким показателям относятся абсолютный прирост, темп роста и прироста, абсолютное значение 1% прироста. При этом принято сравниваемый уровень называть отчетным, а уровень, с которым сравнивают, - базисным. К абсолютным аналитическим показателям относятся абсолютный прирост и абсолютное значение 1% прироста.
Абсолютный прирост ( 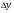 ) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста: ) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста: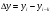 , где , где 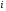 =1, 2, 3, …, =1, 2, 3, …, 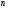 . . Если 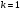 , то уровень , то уровень  является предыдущим для данного ряда, а абсолютные приросты изменения будут цепными. Если же является предыдущим для данного ряда, а абсолютные приросты изменения будут цепными. Если же 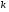 постоянно для данного ряда, то абсолютные приросты будут базисными. постоянно для данного ряда, то абсолютные приросты будут базисными.
Абсолютное значение 1% прироста представляет собой одну сотую часть базисного уровня и в то же время – отношение абсолютного прироста к соответствующему темпу прироста: 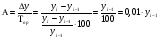 , где , где 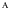 - обозначение абсолютного значения 1% прироста. - обозначение абсолютного значения 1% прироста.Абсолютное значение 1% прироста служит косвенной мерой базисного уровня и вместе с темпом прироста позволяет рассчитать абсолютный прирост уровня за рассматриваемый период, т.е. показывает, сколько абсолютных единиц приходится на 1% прироста. Билет №18. Производные относительные показатели динамического ряда. Коэффициент роста Ki определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста (Ti). Коэффициент роста базисный Коэффициент роста цепной Темп роста Темп прироста ТП определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному. Темп прироста базисный Темп прироста цепной Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей):
Билет №19. Среднегодовые показатели роста и прироста (абсолютные и относительные). Для характеристики динамики изучаемого явления за продолжительный период рассчитывают группу средних показателей динамики. Можно выделить две категории показателей в этой группе: а) средние уровни ряда; б) средние показатели изменения уровней ряда. Средние уровни ряда рассчитываются в зависимости от вида временного ряда. Для интервального ряда динамики абсолютных показателей средний уровень ряда рассчитывается по формуле простой средней арифметической: Для моментного динамического ряда средний уровень определяется следующим образом. Средний уровень моментного ряда с равными интервалами рассчитывается по формуле средней хронологической: 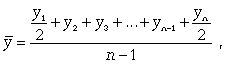 где n - число дат. где n - число дат.Средний уровень моментного ряда с неравными интервалами рассчитывается по формуле средней арифметической взвешенной, где в качестве весов берется продолжительность промежутков времени между временными моментами изменений в уровнях динамического ряда: Средний абсолютный прирост (средняя скорость роста) определяется как средняя арифметическая из показателей скорости роста за отдельные периоды времени: Средний коэффициент роста ( Средний коэффициент роста можно определить иначе: 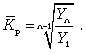 Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах: Средний темп прироста Среднее абсолютное значение 1% прироста можно рассчитать по формуле 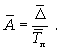 Билет №20. Способы обработки динамических рядов. Выделяют 3 основных способа обработки динамического ряда: а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала; б) метод скользящей средней; в) аналитическое выравнивание. Укрупнение интервалов - наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней. По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев расcчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической. Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Первую рассчитанную центрированную относят ко второму периоду, вторую - к третьему, третью - к четвертому и т.д. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом: Аналитическое выравнивание – построение аналитической функции. Билет №21. Интерполяция и экстраполяция в динамических рядах. Исследование динамики соц.эк. явлений создает базу для прогнозирования т.е. для определения ориентированных размеров уровней явления в будущем. Интерполяция: определение отсутствующего уровня внутри динамического ряда .Возможные методы определения неизвестных значений:1) полусумма уровней, расположенных рядом с интерполируемыми;2)определение по среднему абсолютному приросту; определение по коэффициенту роста. Экстраполяция: определение уровней, выходящих за пределы ряда. Перенесение основной тенденции развития или тренда на будущие периоды. Экстраполирование используется для прогнозирования факторов, способных влиять на развитие явления в будущем. Интерполяция 1) Ср. арифм. 2х соседних уровней.Y2000 = (Y2001 + Y1999)/2 2) Среднегодовой абсолютный прирост.Δy=(Y2006 -Y1999)/N-1а) Y2000 = Y1999 + Δyб) Y2000 = Y 2001 – Δy 3) Среднегодовой коэффициент роста 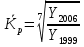 а) Y2000 = Y1999 * Kpб) Y2000 = Y 2001 / Kp. а) Y2000 = Y1999 * Kpб) Y2000 = Y 2001 / Kp.Экстраполяция 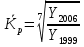 1) Y2007 = Y2006 + Δy , Y2007 = Y2006 * Kp 1) Y2007 = Y2006 + Δy , Y2007 = Y2006 * KpБилет №22. Значение экономических индексов и их классификация. Индекс – особый статистический относительный показатель, характеризующий соотношение во времени или пространстве различных социально-экономических явлений. Например: Ip = 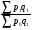 - агрегатный индекс цен с весами текущего периода (формула Пааше); - агрегатный индекс цен с весами текущего периода (формула Пааше);Iq = 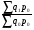 - агрегатный индекс физического объема с весами базисного (предыдущего) периода (формула Ласпейреса). - агрегатный индекс физического объема с весами базисного (предыдущего) периода (формула Ласпейреса).Классификация индексов 1) по степени охвата По степени охвата различают индивидуальные, сводные (общие) и групповые индексы. А) Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления, например изменения объема производства отдельных видов продукции. Б) Сводные индексы рассчитываются для измерения динамики сложного явления, составные части которого непосредственно несоизмеримы, например изменения физического объема продукции, включающей разноименные товары. В) Групповые индексы охватывают не все элементы сложного явления, а только часть их, например физический объем продукции по отдельным отраслям промышленности. Групповые индексы отражают закономерности в развитии отдельных частей изучаемых явлений. 2) по базе сравнения По базе сравнения все индексы делятся на динамические и территориальные. А) Динамические индексы отражают изменение явления во времени. Например, индекс цен на продукцию в 2007г. по сравнению с предыдущим годом. При исчислении динамических индексов происходит сравнение значения показателя в отчетный период со значением этого же показателя за предыдущий (базисный) период. Динамические индексы, как и ряды динамики, бывают базисными и цепными. Базисные динамические индексы – результат сравнения текущих уровней с одним фиксированным уровнем, принятым за базу. Например, Iq = 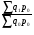 ; I’q = ; I’q = 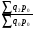 ; ; I’’q = 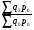 - базисные индексы Ласпейреса. - базисные индексы Ласпейреса.Цепные динамические индексы – результат сравнения текущих уровней с непосредственно предшествующими. Например, Ip = 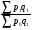 ; I’p = ; I’p =  ; ; I’’p = 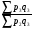 - цепные индексы Пааше. - цепные индексы Пааше. Б) Территориальные индексы применяются для межрегиональных сравнений. Эти индексы имеют большое значение в международной статистике при сопоставлении показателей социально-экономического развития разных стран. Например, индекс цен на автомобили в США по сравнению с Японией. 3) по виду весов Вес индекса – величина постоянная, одинаковая в числителе и знаменателе, служит для соизмерения индексируемых величин. По виду весов индексы бывают с постоянными и переменными весами. А) Постоянный вес – вес базисного периода. С постоянными весами рассчитываются индексы физического объема продукции (индекс Ласпейреса, где p0 – постоянный вес). Б) Переменный вес – вес текущего периода. С переменными весами рассчитываются индексы цен (индекс Пааше, где q1 – переменный вес). 4) В зависимости от формы построения В зависимости от формы построения различаются индексы агрегатные и средние. А) Агрегатный индекс – сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина – признак, изменение которого изучается), а другая остается неизменной в числителе и знаменателе (вес индекса). Агрегатные индексы – основная форма общих индексов. Пример: Ip = 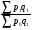 - агрегатный индекс цен с весами текущего периода (формула Пааше). - агрегатный индекс цен с весами текущего периода (формула Пааше).Б) Средние индексы – производные, они получаются в результате преобразования агрегатных индексов, а следовательно, тождественны им. Средний индекс вычисляется как средняя величина из индивидуальных индексов. Средние индексы делятся наарифметические и гармонические. a) Средний арифметический индекс тождествен агрегатному индексу, только если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Например, Iq = 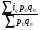 - средний арифметический индекс физического объема продукции, где весом является стоимость продукции базисного периода, также как и в формуле Iq = - средний арифметический индекс физического объема продукции, где весом является стоимость продукции базисного периода, также как и в формуле Iq = 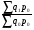 . Так как iq . Так как iq q0 = q1, то обе формулы могут быть преобразованы друг в друга. q0 = q1, то обе формулы могут быть преобразованы друг в друга.b) Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса. Например, Ip = 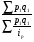 - средний гармонический индекс цен, где весом является стоимость продукции текущего периода, также как и в формуле Ip = - средний гармонический индекс цен, где весом является стоимость продукции текущего периода, также как и в формуле Ip = 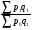 . . Так как 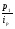 = p0, то обе формулы могут быть преобразованы друг в друга. = p0, то обе формулы могут быть преобразованы друг в друга.5) по характеру объекта исследования По характеру объекта исследования общие индексы подразделяются на индексы количественных и качественных показателей. В основе такого деления лежит вид индексируемой величины. К первой группе, например, относятся индексы объема продаж долларов США на ММВБ, а ко второй – индекс курса немецкой марки. 6) по объекту исследования по объекту исследования индексы бывают: производительности труда, себестоимости, физического объема продукции, стоимости продукции и т.д. 7) по составу явления По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава и переменного состава. А) Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Индекс переменного состава отражает изменение не только индексируемой величины, но и структуры совокупности (весов). Например: Iпс = 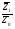 = = 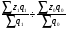 - индекс переменного состава себестоимости продукции. - индекс переменного состава себестоимости продукции.Б) Индекс постоянного состава – индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Индекс фиксируемого состава определяется как агрегатный индекс. Например: Iфс =  = =  - индекс фиксированного состава себестоимости продукции. - индекс фиксированного состава себестоимости продукции.8) по периоду исчисления По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные. Билет №23. Индивидуальные индексы стоимости (товарооборота), цен, физического объема. Индивидуальные индексы получают в результате сравнения однотоварных явлений. Например, индекс цен на растительное масло определяется как отношение цены на этот товар в текущем периоде к цене базисного периода. В зависимости от экономического значения индивидуальные индексы бывают физического объема продукции, цен, товарооборота и т.д. 1) Индивидуальный индекс физического объема продукции Индивидуальный индекс физического объема продукции iq рассчитывается по формуле: iq =  , где q1 – физический объем данного товара в текущем периоде, а q0 – физический объем данного товара в базисном периоде. , где q1 – физический объем данного товара в текущем периоде, а q0 – физический объем данного товара в базисном периоде.Этот индекс показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько процентов составляет рост (снижение) выпуска товара. Если из значения индекса, выраженного в процентах, вычесть 100%, то полученная величина покажет, на сколько процентов возрос (уменьшился) выпуск продукции. 2) Индивидуальный индекс цен Индивидуальный индекс цен ip рассчитывается по формуле ip = 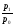 , где p1 – цена на данный товар в текущем периоде, а p0 – цена на данный товар в базисном периоде. Таким образом, этот индекс характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным. , где p1 – цена на данный товар в текущем периоде, а p0 – цена на данный товар в базисном периоде. Таким образом, этот индекс характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным.3) Индивидуальный индекс стоимости продукции Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на ее цену (p). Индивидуальный индекс стоимости продукции ipq рассчитывается по формуле ipq = 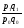 , где p1q1 – стоимость данного товара в текущем периоде, а p0q0 – стоимость данного товара в базисном периоде. , где p1q1 – стоимость данного товара в текущем периоде, а p0q0 – стоимость данного товара в базисном периоде.Этот индекс отражает, во сколько раз изменилась стоимость какого-либо товара в текущем периоде по сравнению с базисным или сколько процентов составляет рост (снижение) стоимости товара. При этом: ip  iq= ipq iq= ipqБилет №24. Построение индексов в агрегатной форме. Индексируемая величина и статистический вес. Агрегатный индекс – сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Особенность этой формы индекса состоит в том, что в агрегатной форме непосредственно сравниваются две суммы одноименных показателей. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной в числителе и знаменателе (вес индекса). Агрегатные индексы – основная форма общих индексов. Индексируемая величина – признак, изменение которого изучается (цена товаров, курс акций и т.д.) Вес индекса – величина постоянная, одинаковая в числителе и знаменателе, служит для соизмерения индексируемых величин. Методика построения агрегатного индекса предусматривает ответ на три вопроса: А) какая величина будет индексируемой; Б) по какому составу разнородных элементов явления необходимо исчислить индекс; В) что будет служить весом при расчете индекса. При этом, если строится индекс количественного показателя, то веса берутся за базисный период; при построении индекса качественного показателя используются веса отчетного периода. 1) Агрегатный индекс стоимости продукции Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на ее цену (p). Индекс стоимости продукции, или товарооборота (Ipq) представляет собой отношение стоимости продукции текущего периода (  ) к стоимости продукции в базисном периоде ( ) к стоимости продукции в базисном периоде (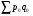 ) и определяется по формуле: Ipq = ) и определяется по формуле: Ipq =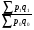 . .Такой индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции. Если из значения индекса стоимости вычесть 100% (Ipq – 100%), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. Разность числителя и знаменателя (  - -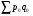 ) показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. ) показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. 2) Агрегатный индекс физического объема продукции Индекс физического объема продукции – это индекс количественного показателя. Здесь индексируемая величина – количество продукции в натуральном выражении, а вес – цена. Только умножив несоизмеримые между собой количества разнородной продукции на их цены, можно перейти к стоимостям продукции, которые будут уже величинами соизмеримыми. Так как индекс физического объема – индекс количественного показателя, то весами будут цены базисного периода. Тогда формула индекса примет следующий вид: Iq = 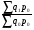 , где в числителе дроби – условная стоимость произведенных в текущем периоде товаров в ценах базисного периода, а в знаменателе – фактическая стоимость товаров, произведенных в базисном периоде. , где в числителе дроби – условная стоимость произведенных в текущем периоде товаров в ценах базисного периода, а в знаменателе – фактическая стоимость товаров, произведенных в базисном периоде.Данный индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема ее производства или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения физического объема ее производства. Если из значения этого индекса вычесть 100% (Iq – 100%), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным из-за роста (снижения) объема ее производства. Разность числителя и знаменателя ( 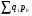 - - 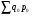 ) показывает, на сколько рублей изменилась стоимость продукции в результате роста (уменьшения) ее объема. ) показывает, на сколько рублей изменилась стоимость продукции в результате роста (уменьшения) ее объема.3) Агрегатный индекс цен Индекс цен является наиболее широко распространенным показателем инфляции. Индекс цен – индекс качественного показателя. Индексируемая величина – цена товара, вес – количество произведенных товаров. Умножив цену товара на его количество, получаем величину, которую можно суммировать и которая представляет собой показатель, соизмеримый с другими подобными ему величинами. Так как индекс цен – индекс качественного показателя, то весом будет количество произведенной продукции текущего периода. Тогда индекс цен определяется по следующей формуле: Ip= 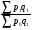 , где в числителе дроби – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров в ценах базисного периода. , где в числителе дроби – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров в ценах базисного периода.Индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен. Если из значения данного индекса вычесть 100% (Ip - 100%), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции из-за изменения цен, а разность числителя и знаменателя (  - -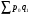 ) – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен. ) – на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен.При этом: Ip  Iq= Ipq Iq= IpqБилет №25. Средние индексы, тождественные агрегатным. Кроме агрегатных, индексов в статистике применяются и средневзвешенные. Их рассчитывают, если имеющейся информации недостаточно, чтобы рассчитать общий агрегатный индекс. Например, если нет данных о ценах, но есть – о стоимости продукции в текущем периоде и об индивидуальных индексах цен по каждому товару, то общий индекс цен как агрегатный определить нельзя, но можно вычислить его как средний из индивидуальных. Если же не известны количества произведенных отдельных видов продукции, но известны индивидуальные индексы и стоимость продукции базисного периода, то можно определить общий индекс физического объема как средневзвешенную величину. Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. Средний индекс производный, он получается в результате преобразования агрегатного, а следовательно тождествен ему. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая. Средний арифметический индекс тождествен агрегатному, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Средний арифметический индекс физического объема вычисляется по формуле: 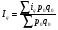 . Весами в формуле является стоимость продукции базисного периода. Так как . Весами в формуле является стоимость продукции базисного периода. Так как  , то формула этого индекса легко преобразуется в формулу: , то формула этого индекса легко преобразуется в формулу:  . . Средние арифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей. Индексы качественных показателей обычно определяются по формуле средней гармонической взвешенной величины. Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса. Например, индекс цен можно вычислить по формуле: 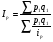 , где весами является стоимость продукции текущего периода. Так как , где весами является стоимость продукции текущего периода. Так как 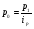 , то формула может быть легко преобразована в формулу , то формула может быть легко преобразована в формулу 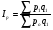 . . Средние индексы также широко применяются для анализа рынка ценных бумаг. Наиболее известным является индекс Доу-Джонса, который определяется как средний арифметический индекс значений курсов акций, котирующихся на Нью-йоркской фондовой бирже. Билет №26. Выбор базы и весов при построении индексов. Системы индексов (цепных и базисных). Системой индексов называется ряд последовательно построенных индексов. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение исследуемого периода времени. В зависимости от базы сравнения системы индексов бывают базисными и цепными. Система базисных индексов – это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения, т.е. в знаменателе всех индексов находится индексируемая величина базисного периода. Система цепных индексов – это ряд индексов одного и того же явления, вычисленных с меняющейся от индекса к индексу базой сравнения. В экономико-статистических исследованиях выбор системы индексов (базисные или цепные) проводится в зависимости от цели анализа. Базисные индексы дают более наглядную характеристику общей тенденции развития исследуемого явления, а цепные – четче отражают последовательность изменения уровней во времени. Системы цепных и базисных индексов могут быть построены для индивидуальных и общих индексов. Между цепными и базисными индексами существуют различные виды связи. Если известны цепные индексы, то путем их последовательного перемножения можно получить базисные индексы. Например, 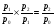 или или 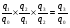 . .Зная последовательные значения базисных индексов, легко рассчитать на их основе цепные индексы. Например, 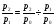 или или 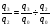 . .Системы базисных и цепных индексов могут быть построены для агрегатных индексов. Например, цепные индексы стоимости: 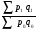 ; ; 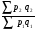 ;…; ;…;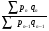 или базисные индексы стоимости: или базисные индексы стоимости: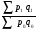 ; ;  ;…; ;…;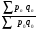 . .Формирование системы индексов цен и физического объема отличаются от рассмотренных выше, т.к. при построении систем этих индексов можно использовать постоянные или переменные веса. Система индексов с постоянными весами – система сводных индексов одного и того же явления, вычисленных с весами, не меняющимися при переходе от одного индекса к другому. Постоянные веса позволяют исключить влияние изменения структуры на величину индекса. Например, система базисных индексов физического объема продукции с постоянными весами ( 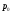 ): ):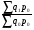 ; ;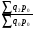 ;…; ;…; - и система цепных индексов физического объема с постоянными весами: - и система цепных индексов физического объема с постоянными весами: 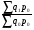 ; ; 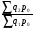 ;…; ;…; . . При этом между цепными и базисными индексами с постоянными весами также существует связь. Например, перемножая цепные индексы получаем соответствующий базисный: 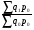  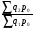 = =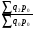 , а при деление базисных индексов получаем соответствующий цепной: , а при деление базисных индексов получаем соответствующий цепной: 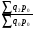  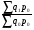 = =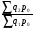 . .Система индексов с переменными весами – система сводных индексов одного и того же явления, вычисленных с весами, последовательно меняющимися от одного индекса к другому. Переменные веса – веса отчетного периода. Например, система базисных индексов цен с переменными весами: 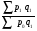 ; ; 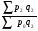 ;…; ;…; 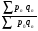 - и система цепных индексов цен с переменными весами: - и система цепных индексов цен с переменными весами: 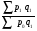 ; ;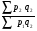 ;…; ;…; . . Для общих индексов рассчитанных с переменными весами взаимосвязь между цепными и базисными индексами отсутствует. Билет №27. Предмет и метод статистики населения, ее задачи. |
