Статистика понятие, ее предмет и метод, основные категории
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
14. Непараметрические методы оценки взаимосвязей. Непараметрическиеметоды не накладывают ограничений на закон распределения изучаемых величин и обычно более просты в вычислениях. Поэтому их применяют и для оценки корреляционных связей, и особенно широко для оценки связи атрибутивных (качественных) признаков. Непараметрические методы оценки связи В методах корреляционного и регрессионного анализа взаимосвязей используются основные характеристики (параметры) распределения – средние значения и дисперсии. Эти методы получили название параметрических. Статистической наукой разработаны и такие методы, с помощью которых можно измерить связь между явлениями, не используя количественные значения признака, а, значит, и параметры распределения. Такие методы получили название непараметрических. При оценке взаимосвязи двух качественных признаков используют представление единиц совокупности в форме так называемых таблиц взаимной сопряженности. Значения коэффициентов показывают наличие заметной связи между изучаемыми признаками. Коэффициент К Чупрова обычно дает более осторожную оценку связи. Взаимосвязь между двумя альтернативными признаками измеряется с помощью 4-х клеточных таблиц. В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить, т.е. ранжировать. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д. При ранжировании каждой единице совокупности присваивается ранг, т.е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Так, если 5-я и 6-я единица совокупности одинаковы, обе единицы получат ранг равный (5+6)/2=5,5. Для измерения связи между ранжированными признаками определяют ранговые коэффициенты корреляции Спирмена () и Кендэлла (). Сущность метода Спирмена в следующем: 1) располагают варианты факторного признака по возрастанию, т.е. ранжируют единицы по значению признака X; 2) для каждой единицы совокупности указывают ранг с точки зрения результативного признака Y. Если связь прямая, то с увеличением ранга признака Х, будет возрастать и ранг Y; при тесной прямой связи ранги признаков Х и Y в основном совпадут. При обратной связи возрастанию рангов признака Х будет соответствовать общее убывание рангов признака Y. Теснота связи между признаками оценивается ранговым коэффициентом корреляции Спирмена: 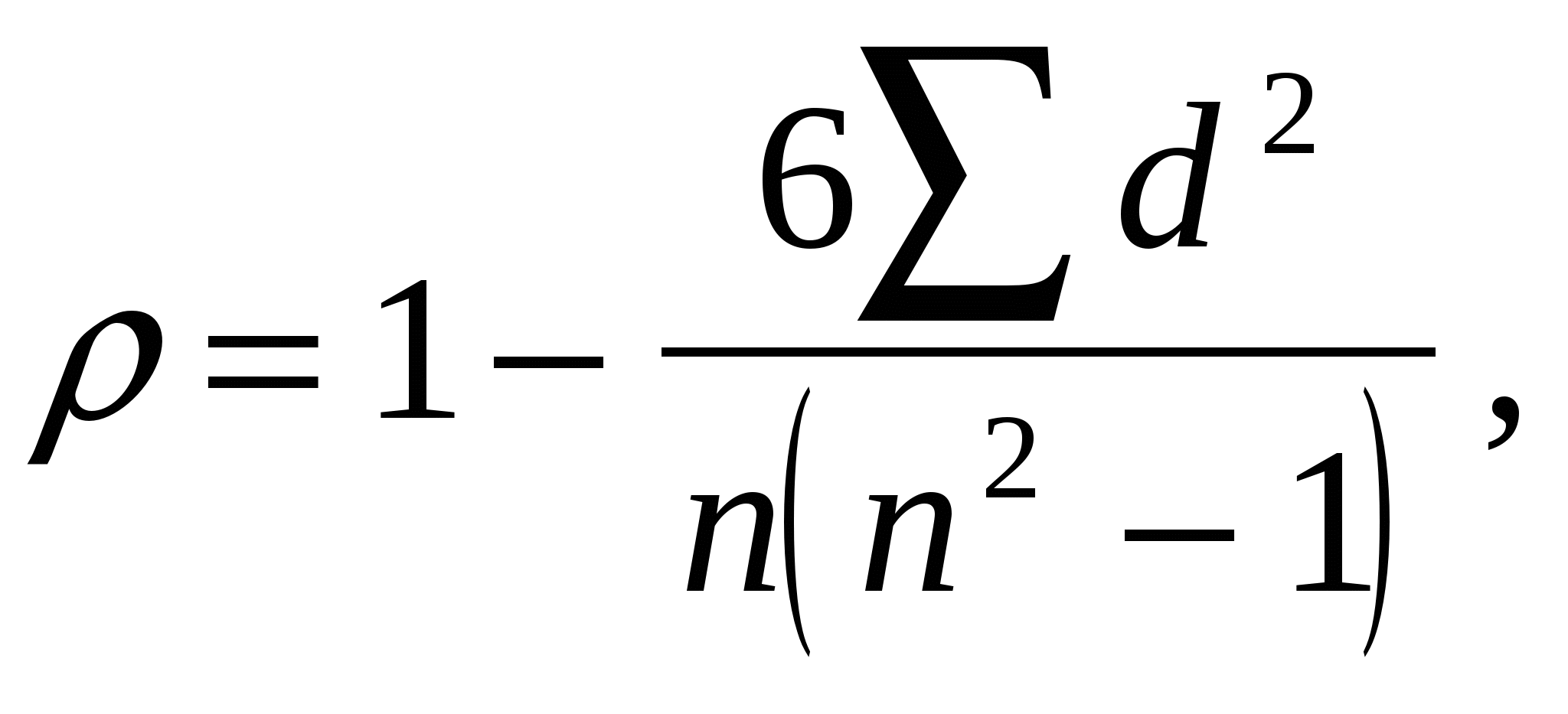 где d – разность рангов признаков Х и Y; n – число наблюдаемых единиц. Кендэллом предложен другой показатель также с использованием рангов: 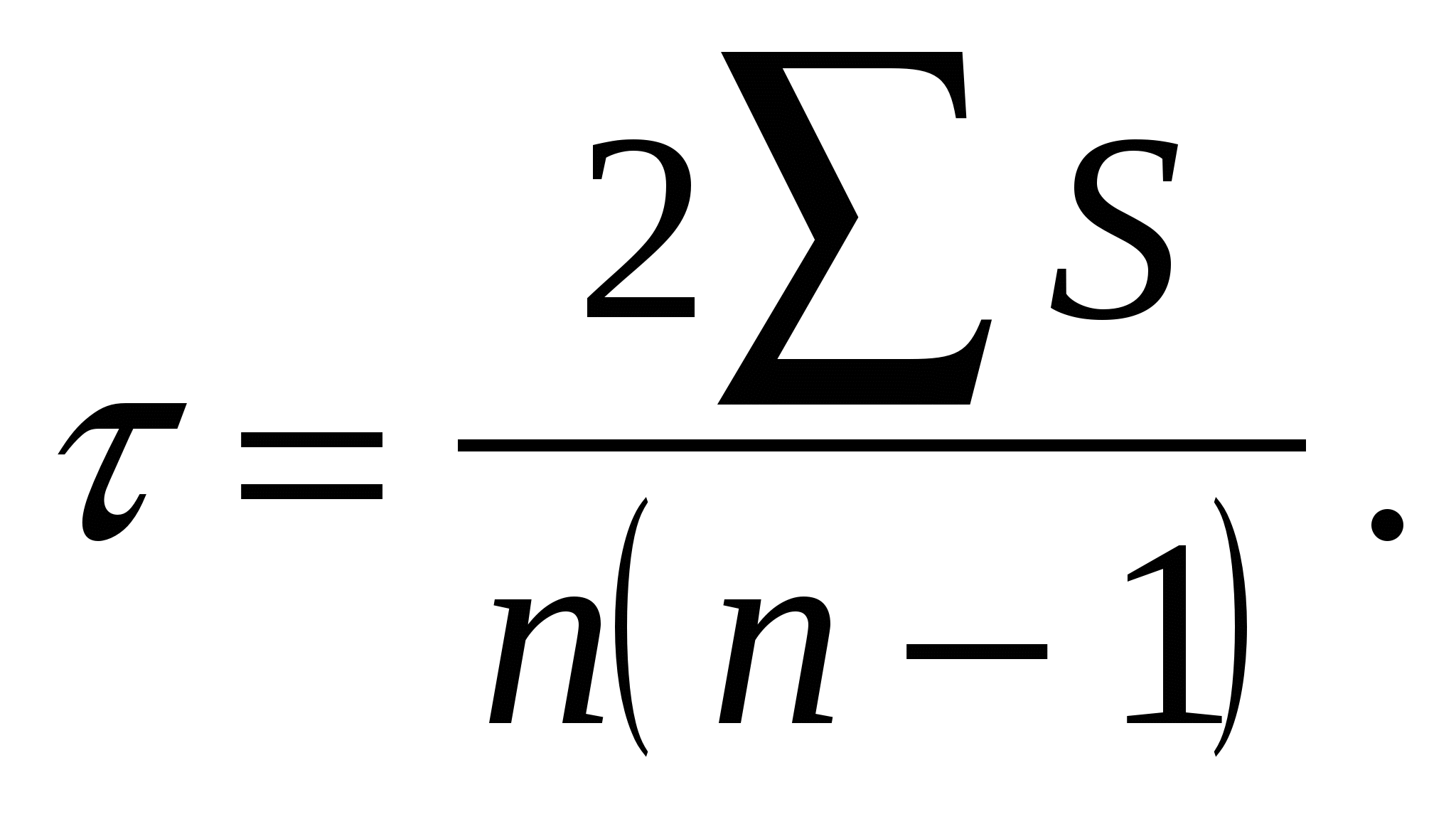 Расчет коэффициента Кендэлла выполняется в следующем порядке. 1. Ряд наблюдений располагается в возрастающем порядке по признаку Х с указанием соответствующих рангов по признаку Y. 2. Упорядоченная таким образом последовательность берется как исходная для построения квадратной матрицы (aij) размерностью (n×n). Далее потребуются только элементы, расположенные выше главной диагонали. По каждой паре наблюдений (i,j) сравниваем ранги признака Y: 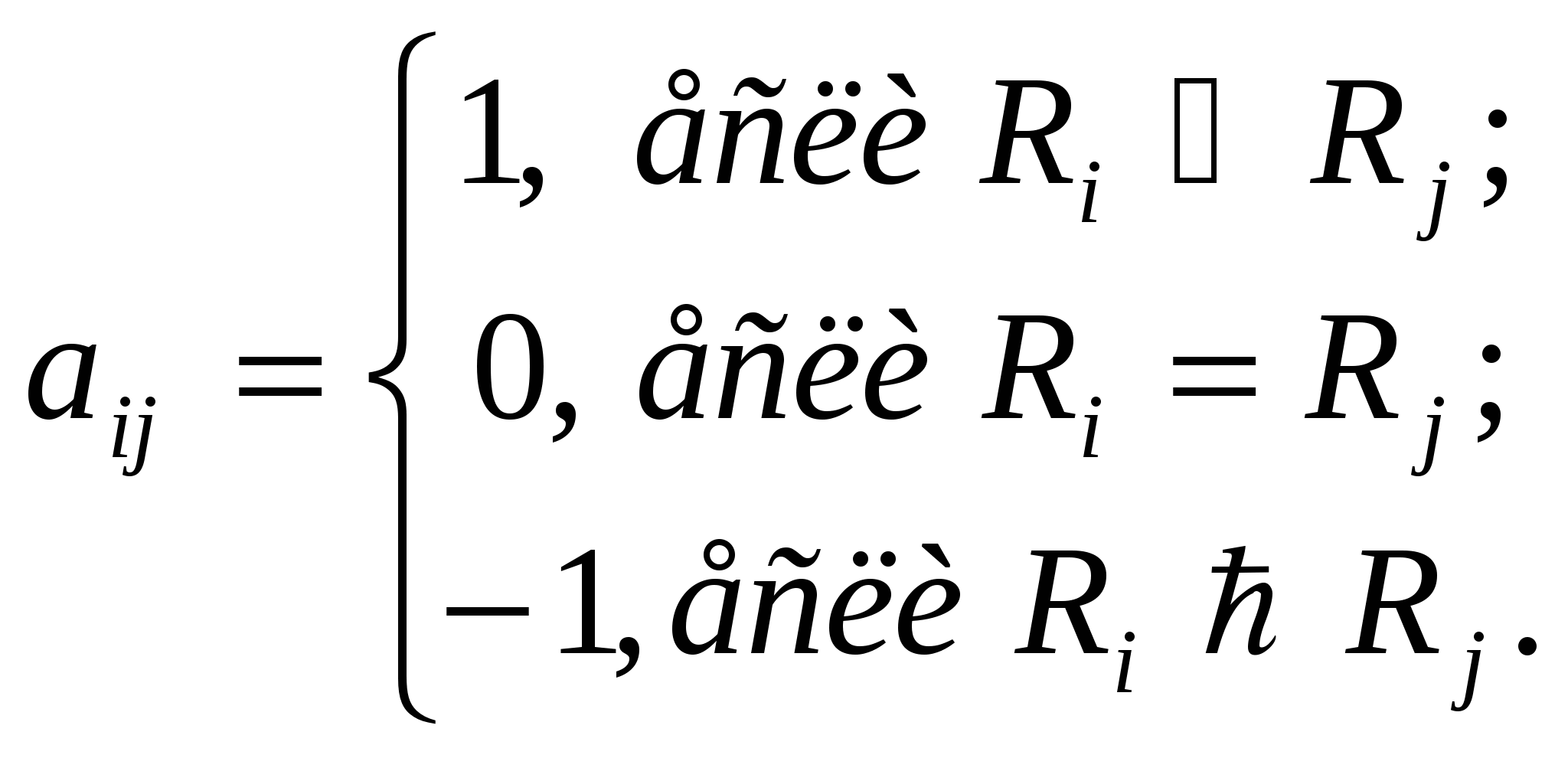 Сумма элементов aij, расположенных выше главной диагонали, и есть искомое значение S в формуле коэффициента Кендэлла. При некотором навыке расчет величины S можно выполнить, непосредственно сравнивая ранг Yданного наблюдения с рангами Y последующих наблюдений. Для каждого наблюдения подсчитываются Р – число случаев, когда ранг признака Y следующих наблюдений меньше, чем у данного, и Q – число случаев, когда у следующих наблюдений ранг признака Y больше, чем у данного. Искомое значение 15. Ранговая корреляция, понятие, методы ее измерения. Метод ранговой корреляции Спирмена позволяет определить силу и направление корреляционной связи между двумя признаками или двумя иерархиями признаков. Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы. Такими рядами могут быть: А) Два признака, измеренные в одной и той же группе переменных (наиболее часто в этом качестве выступает группа людей, которых принято тогда именовать испытуемыми или респондентами. Естественно, под переменными подразумеваются не сами люди, а данные ими ответы на те или иные вопросы.) Б) две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков (скажем, по ответам на пункты анкеты или теста). В) Две групповые иерархии признаков (например, соответствие каких-либо выборов, сделанных одной группой людей выборам другой группы). Г) Индивидуальная и групповая иерархии признаков (например, сопоставление индивидуальной иерархии жизненных ценностей сотрудника усредненному мнению группы на этот же счет; сопоставление последовательности товаров, которые приобрели бы (в среднем) жители города А и города Б при условии получения премии, на которую заранее не рассчитывали.) 9. Ограничения метода ранговой корреляции. По каждой переменной должно быть представлено не менее 5 наблюдений. Верхняя граница выборки – меньше или равна 40. Коэффициент ранговой корреляции Спирмена rs при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленные значения. В идеале оба коррелируемых ряда должны представлять собой две последовательности несовпадающих значений. В случае несоблюдения такого условия вносится поправка на одинаковые ранги (будет дано ниже). Помимо этих ограничений, следует так же помнить об ограничениях корреляционного метода вообще – невозможность обнаружения причинной связи между явлениями. 16. Ряды динамики: понятие, виды, правила построения, элементарные показатели анализа. Ряд динамики (хронологический, динамический, временной) представляет собой последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Классификация:
- моментные – показывает фактическое наличие изучаемого явления в конкретный момент времени; - интервальный – последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. 2. По форме представления уровней – ряды абсолютных, относительных и средних величин. 3. По расстоянию или интервалам времени между датами выделяют полные или неполные хронологические ряды. В полных рядах дата регистрации или момент времени следуют друг за другом через равные интервалы. Неполные – когда принцип равных интервалов не соблюдается. 4. По числу показателей: - изолированные, если ведется анализ во времени одного показателя; - комплексные (многомерные), когда в хронологической последовательности дается система показателей, связанных между собой единством процесса, явления. Правила построения рядов динамики:
а) Исторический метод. Периодизация осуществляется на основе «узаконенной» структуры динамики, при этом обращают внимание на значимые даты и события. б) Метод параллельной периодизации. в) Методы многомерного статистического анализа. 2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. 3. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. 4. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями. Показатели анализа рядов динамики:
Когда за основу сравнения берется начальный уровень ряда, получают базисные показатели. Если же сравнение производится с предыдущим уровнем, то цепные.
17. Средние показатели ряда динамики. 1. Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню: где п или (п+1) – общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень. Если в интервальном временном ряду отрезки времени имеют неравную длительность, то средний уровень рассчитывается по формуле средней арифметической: 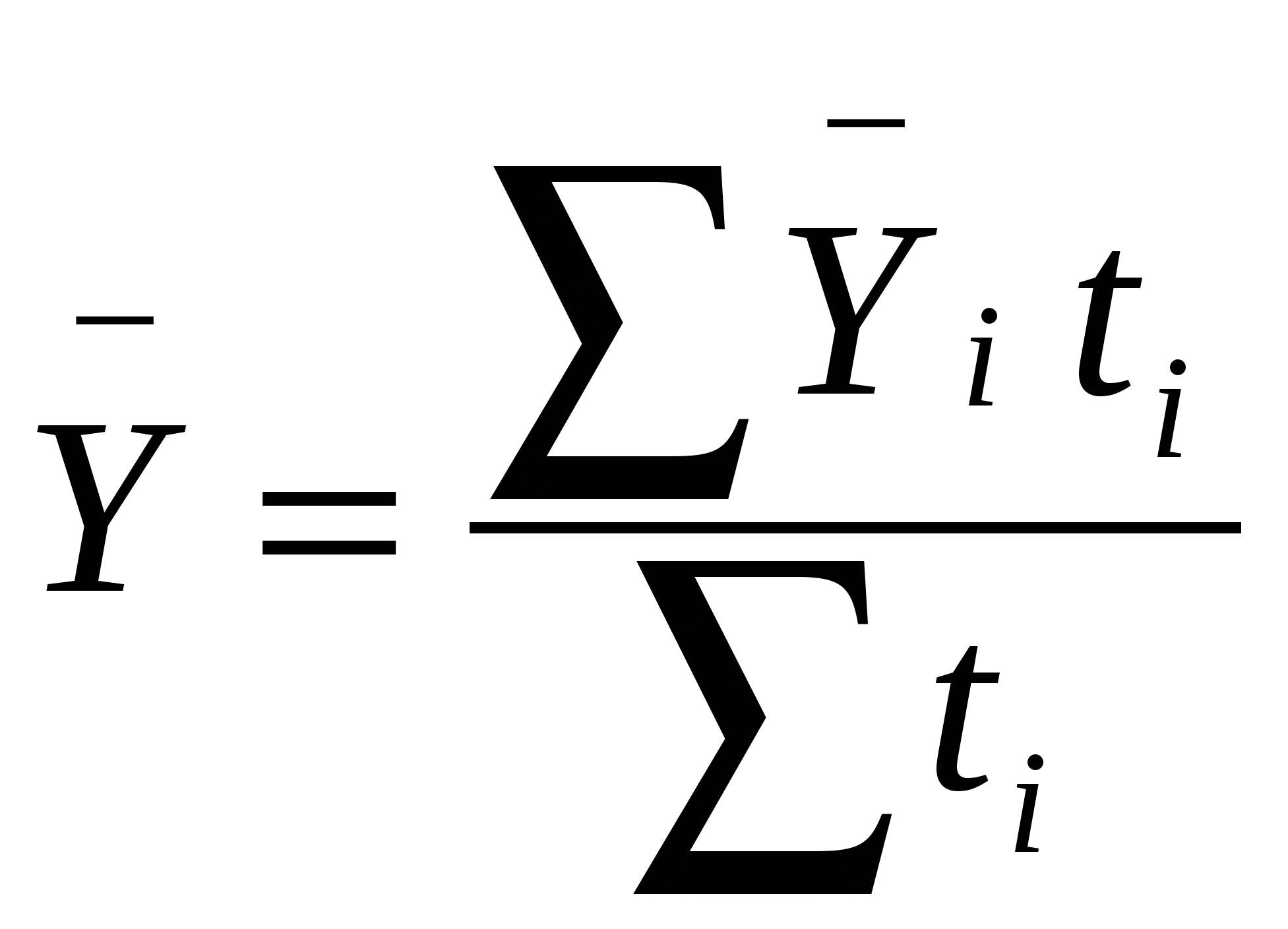 или или Для моментного ряда с равноотстоящими моментами используется формула средней хронологической. Вид формулы определяется способом нумерации уровней. Если уровни нумеруются начиная с нуля, то средняя хронологическая имеет вид 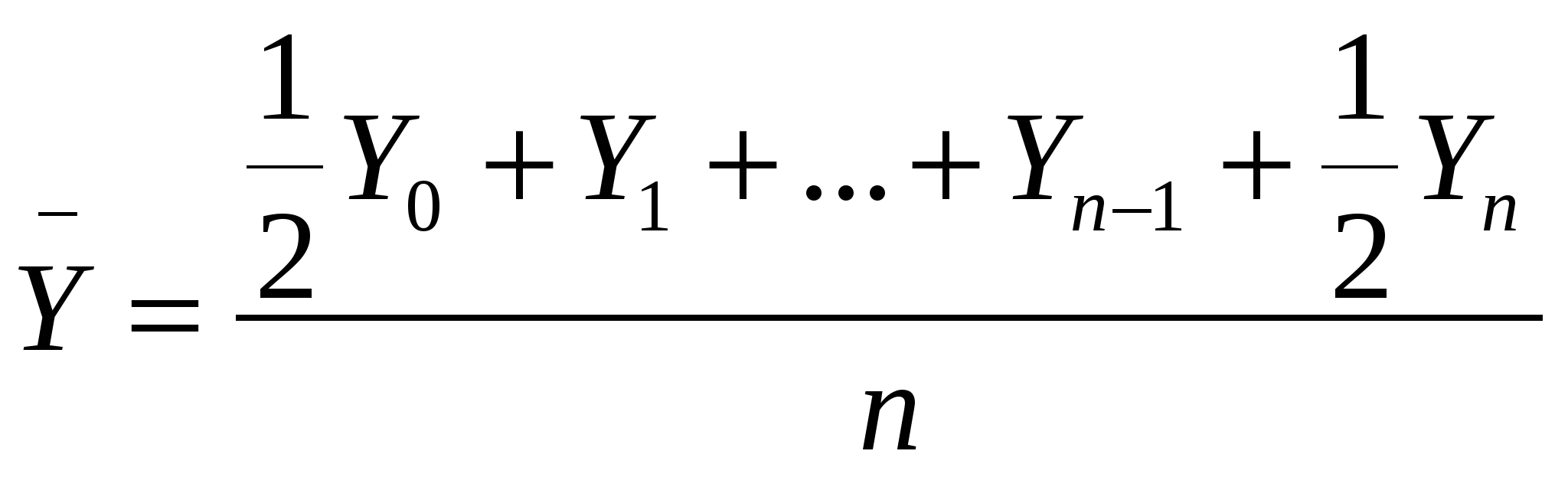 . .Если же уровни обозначены 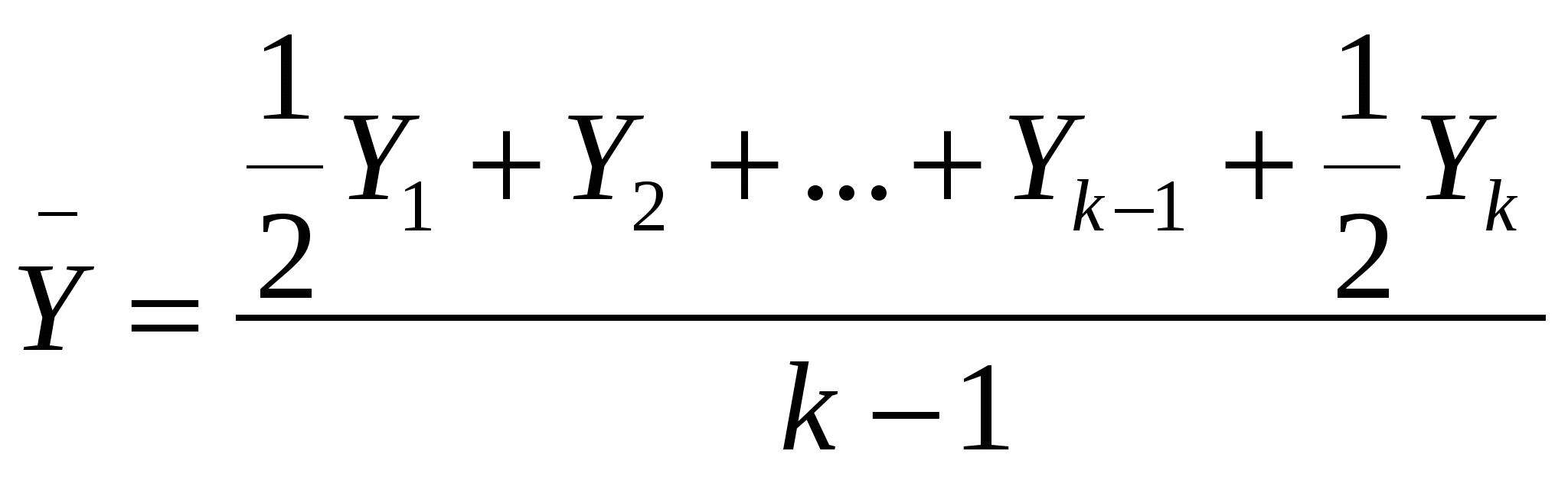 . .Для моментного ряда с неравными интервалами предварительно находятся значения уровней в серединах интервалов: а затем определяется общий средний уровень ряда: 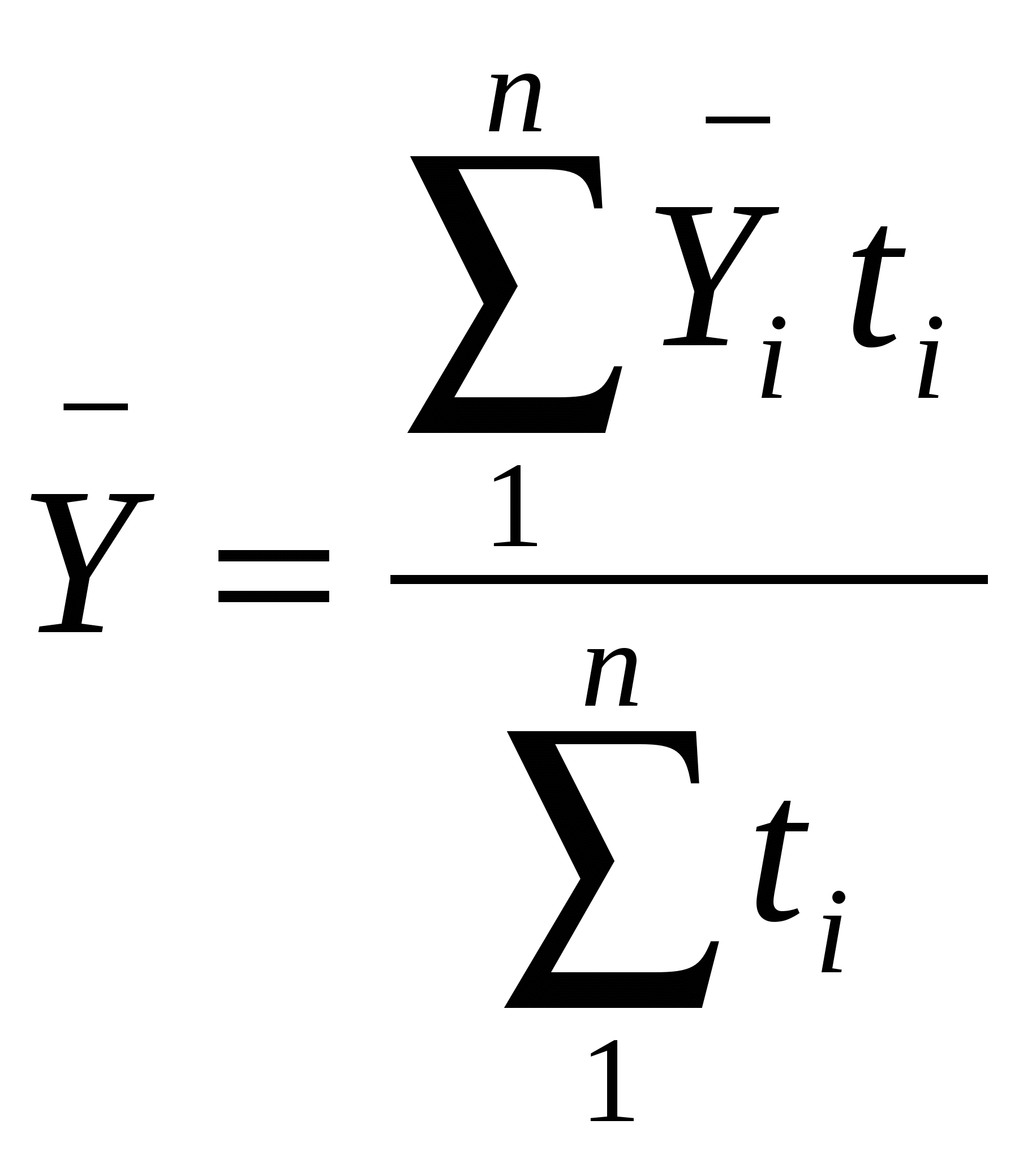 . .2. Средний абсолютный прирост рассчитывается в зависимости от способа нумерации интервалов: 3. Средний темп роста: Если уровни ряда нумеруются от 0 до п, то формула среднего коэффициента роста Если уровни ряда нумеруются от 1 до п, то формула среднего коэффициента роста Здесь Кцеп – цепные коэффициенты роста; Кбаз – базисный коэффициент роста. 4. Средний темп прироста (%): 18. Взаимосвязанные ряды динамики, методы их статистического анализа. Анализ взаимосвязанных рядов динамики Под взаимосвязанными рядами динамики понимают такие, в которых уровни одного ряда в какой-то степени определяют уровни другого. Например, ряд, отражающий внесение удобрений на 1 га, связан с временным рядом урожайности; ряд уровней средней выработки связан с рядом динамики средней заработной платы; ряд среднегодового поголовья молочного стада определяет годовые надои молока и т.д. В простейших случаях анализа исчисляют коэффициенты опережения по темпам роста или прироста. Коэффициенты опережения по темпам роста – это отношение темпов роста (цепных или базисных) одного ряда к соответствующим по времени темпам роста (также цепным или базисным) другого ряда. Аналогично находятся и коэффициенты опережения по темпам прироста Отклонения проверяются и на наличие автокорреляции. Под автокорреляцией понимается зависимость последующих уровней ряда от предыдущих. Для проверки наличия автокорреляции используется критерий Дарбина-Уотсона: 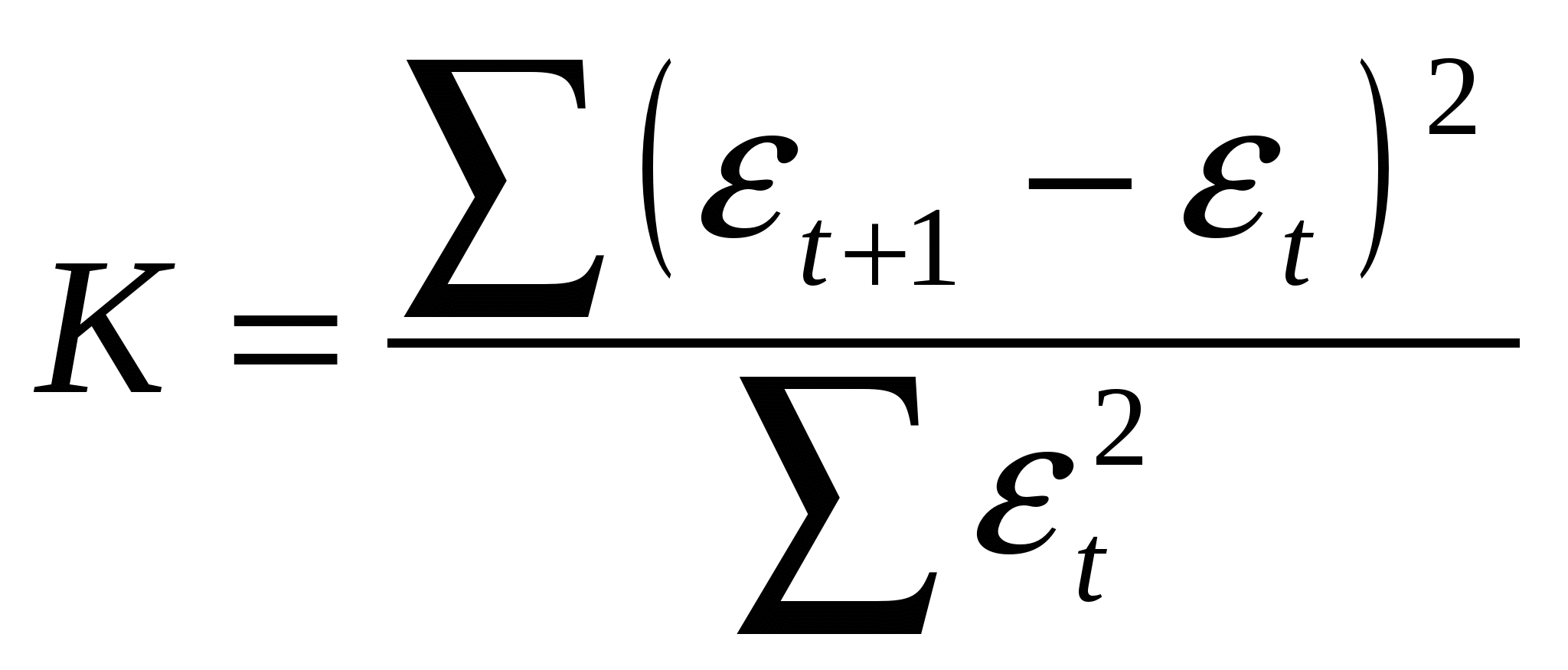 , ,где t – отклонение фактического уровня ряда в точке t от теоретического (выровненного) значения. При К=0 имеется полная положительная автокорреляция, при К=2 автокорреляция отсутствует, при К=4 – полная отрицательная автокорреляция. Если в отклонениях от тенденции подтверждается наличие автокорреляции (положительной или отрицательной), её исключают. Это можно сделать тремя способами. 1. Для каждого из взаимосвязанных рядов динамики Х и Y получают уравнение тренда и рассчитывают отклонения: Для каждой последовательности (t) и (t) выполняется проверка на автокорреляцию по критерию Дарбина-Уотсона. Если значение К близко к 2, то данный ряд отклонений оставляют без изменений. Если же К заметно отличается от 2, то находят параметры уравнения авторегрессии1. Подсчитываются новые остатки: 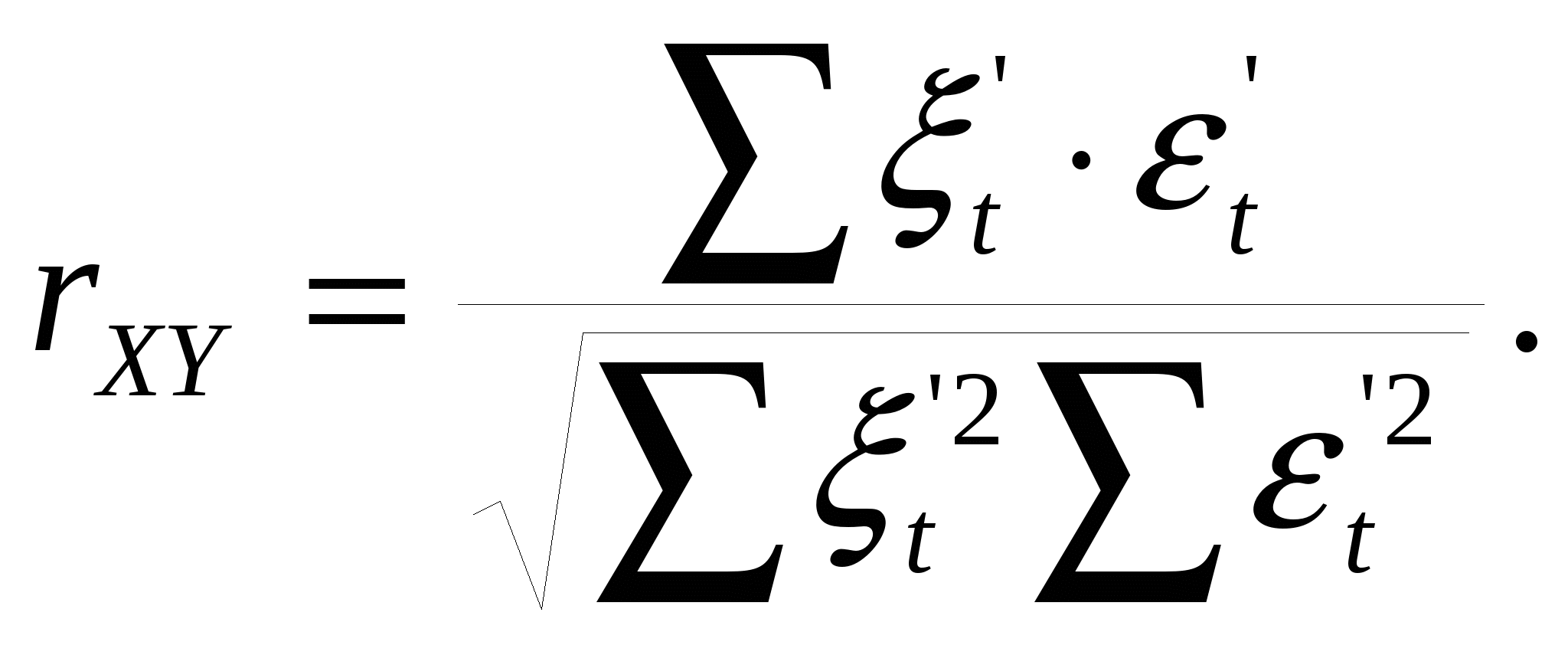 2. Корреляция первых разностей. От исходных рядов динамики Х и Y переходят к новым, построенным по первым разностям: 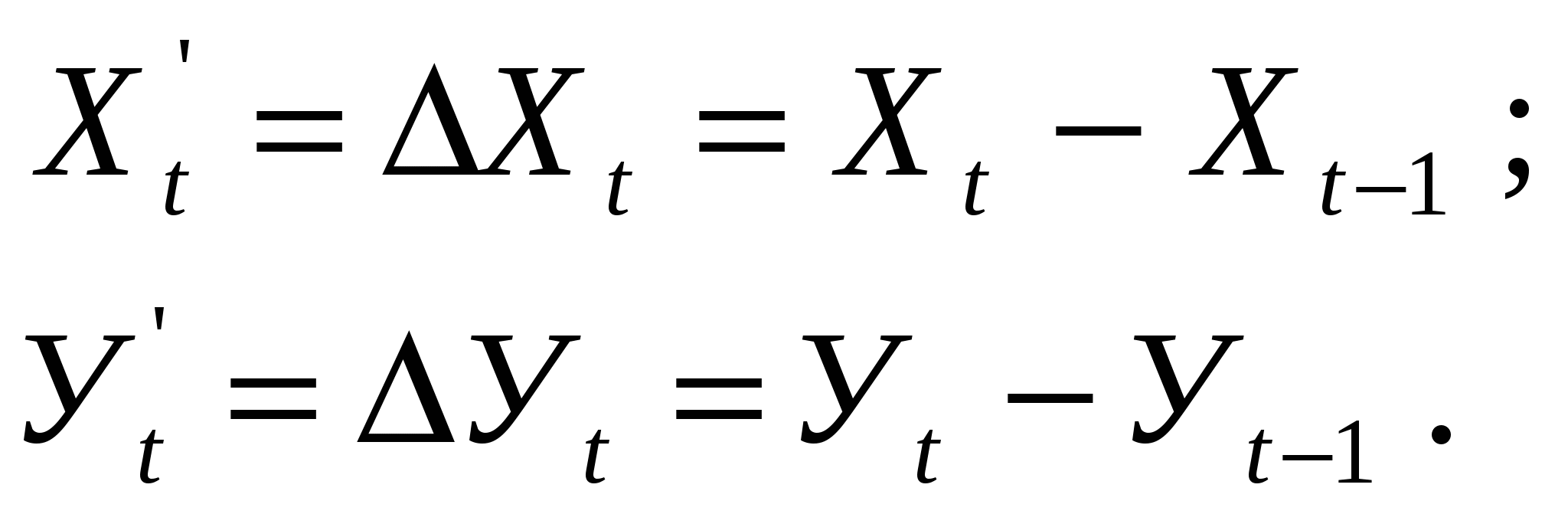 По Х и У определяют направление и силу связи в регрессии: У = f(X) = С0 + С1·Х. 3. Включение времени в уравнение связи. Уt = f(Xt, t). В простейших случаях уравнение выглядит следующим образом: Yt = а0 + а1·Xt + a2∙t. 19. Методы выявления тенденций развития в рядах динамики. Проверка ряда на наличие тренда может выполняться несколькими методами. 1. Метод средних. Изучаемый ряд динамики разбивается на несколько интервалов (обычно на два), для каждого из которых определяется средняя величина. Выдвигается гипотеза о существенном различии средних. Если эта гипотеза принимается, то признается наличие тренда. В более мощном критерии Кокса и Стюарта весь анализируемый ряд динамики разбивают на три группы и сравнивают между собой уровни первой и последней групп. 2. Метод серий. По этому способу каждый конкретный уровень временного ряда считается принадлежащим к одному из двух типов 3. Графический метод. Для подтверждения наличия или отсутствия тренда часто достаточно представить уровни временного ряда на графике (см. тему «Статистические графики»). Графическая иллюстрация развития во времени считается достаточно убедительной. |
