Статистика понятие, ее предмет и метод, основные категории
 Скачать 0.83 Mb.
|
|
Непосредственное выделение тренда может быть выполнено тремя методами. 1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету средних уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов). 2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Количество уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек). При нечетном сглаживании каждое полученное среднее арифметическое значение закрепляют за серединой интервала. При обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только по 50 %; полученное среднее арифметическое значение также закрепляют за серединой каждого расчетного интервала. Последовательно передвигая интервал сглаживания получают последовательность средних (скользящих) значений. 3. Аналитическое выравнивание. Под этим понимается определение аналитического выражения, формулы – f(t) для основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает как бы в зависимости только от течения времени t. Отклонения конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. Трендовая модель имеет вид Уt = f(t) + t , где f(t) – уровень, определяемый тенденцией развития (трендовая составляющая); t – случайное и циклическое отклонение от тенденции В процессе аналитического выравнивания определяется конкретный вид и параметры аналитической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. 20. Сезонные колебания в рядах динамики: понятие, статистические методы их изучения. Если в анализируемой временной последовательности наблюдаются устойчивые систематические отклонения от тенденции, то можно предположить наличие в этом ряду некоторых (одного или нескольких) колебательных процессов. Это особенно заметно, когда изучаемые явления имеют сезонный характер, – возрастание или убывание уровней повторяется регулярно с интервалом в один год (например, производство молока и мяса по месяцам года, потребление топлива и электроэнергии для бытовых нужд, сезонная продажа товаров и т.д.). Уровень сезонности оценивается с помощью индексов сезонности и гармонического анализа Индексы сезонности показывают, во сколько раз фактический уровень ряда в момент или интервал времени t больше среднего уровня либо уровня, вычисляемого по уравнению тенденции f(t). При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет. Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов нескольких лет. Индексы сезонности – это, по существу, относительные величины координации, когда за базу сравнения принят либо средний уровень ряда, либо уровень тенденции. Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции. Если тренда нет или он незначителен, то для каждого месяца (квартала)  ,где Уt – уровень показателя за месяц (квартал) t; Уср – общий средний уровень показателя. Для обеспечения устойчивости показателей можно взять больший промежуток времени. В этом случае за Т лет рассчитывают: 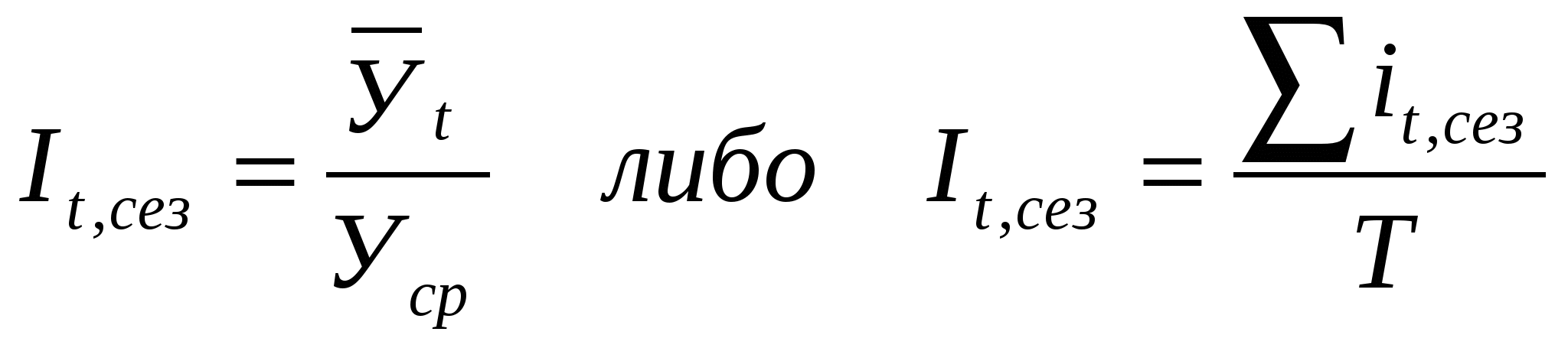  ,где  – средний уровень показателя по одноименным месяцам за ряд лет.Другим методом изучения уровня сезонности является гармонический анализ. Его выполняют, представляя временной ряд как сумму гармонических колебательных процессов. Для каждой точки этого ряда справедливо выражение  , t=1, 2, .... Т.Здесь Yt – фактический уровень ряда в момент (интервал) времени t; f(t) – выровненный уровень ряда в тот же момент (интервал) t; an, bn – параметры колебательного процесса (гармоники) с номером n. Эти параметры в совокупности оценивают размах (амплитуду) отклонений от общей тенденции и сдвиг колебаний относительно начальной точки. Общее число колебательных процессов, которые можно выделить для ряда, состоящего из Т уровней, равно Т/2. Обычно ограничиваются меньшим числом наиболее важных гармоник. Расчеты параметров гармоники достаточно трудоемки и выполняются в настоящее время на компьютерах по известным формулам математического анализа. Аппарат гармонического анализа позволяет оценить роль каждого колебательного процесса в общей вариации уровней временного ряда. Удельный вес гармоники с номером n определяется как dn = Дn / Д, где Д – дисперсия ряда, рассчитанная обычным способом; Дn–дисперсия, вносимая колебательным процессом (гармоникой) с номером n:  21. Агрегатный индекс как основная форма общих индексов. Индекс – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Если известно, что изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, анализ выполняют посредством так называемых общих индексов. Индекс выступает как общий, когда в расчетной формуле показывается неоднородность изучаемой совокупности. Примером неоднородной совокупности является общая масса проданных товаров всех или нескольких видов. Тогда сумму выручки можно записать в виде агрегата (суммы произведений взвешивающего показателя на объемный), например:  .Отношение агрегатов, построенных для различных условий, дает общий индекс показателя в агрегатной форме. Так, например, индекс динамики общего объема товарооборота в агрегатной форме:  .Прирост товарооборота объясняется изменением уровня цен и количества проданных товаров. Влияние на прирост товарооборота общего изменения цен выражается агрегатным индексом цен  , который в предположении первичности изменения количественного показателя (q) и вторичности- качественного (p) имеет вид .Влияние на прирост товарооборота изменения количества проданных товаров отражается агрегатным индексом физического объема  , который строится в положении первичности изменения количественных показателей (q) и вторичности влияния качественных (p): .22. Общие индексы как средние из индивидуальных индексов. Общий индекс можно получить как среднее значение соответствующих индивидуальных индексов. В этом смысле общим индексом отражаются результаты изменения уровня явления у отдельных единиц совокупности. При расчете общего индекса как средней величины веса индивидуальных индексов подбираются так, чтобы был возможен алгебраический переход от общего индекса в форме средней величины к общему индексу в агрегатной форме. Например, индекс общего объема товарооборота можно представить средней арифметической величиной:  .Тот же индекс может быть записан в форме средней гармонической величины: 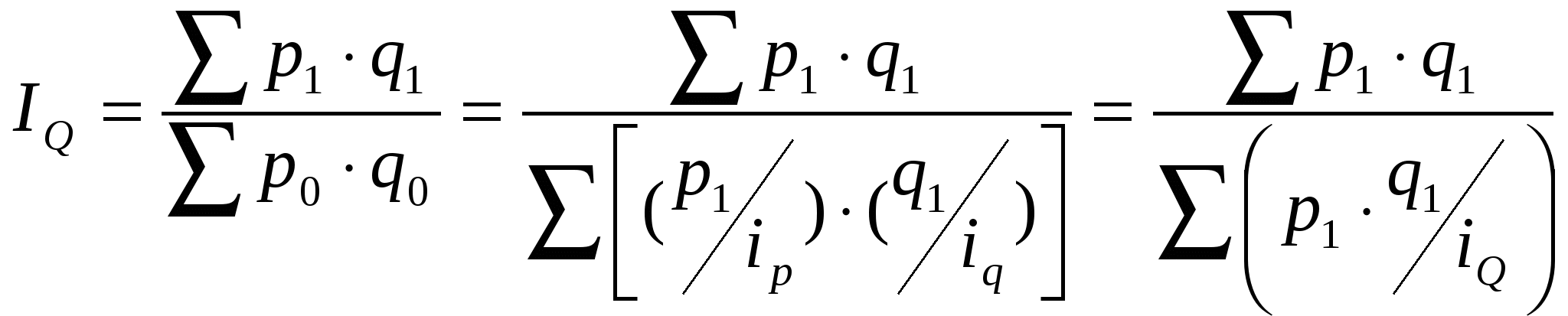 .23. Индексы средних величин: индексы переменного, постоянного составов, влияние структурных сдвигов. Отношение средник величин называется в статистике индексом переменного состава: 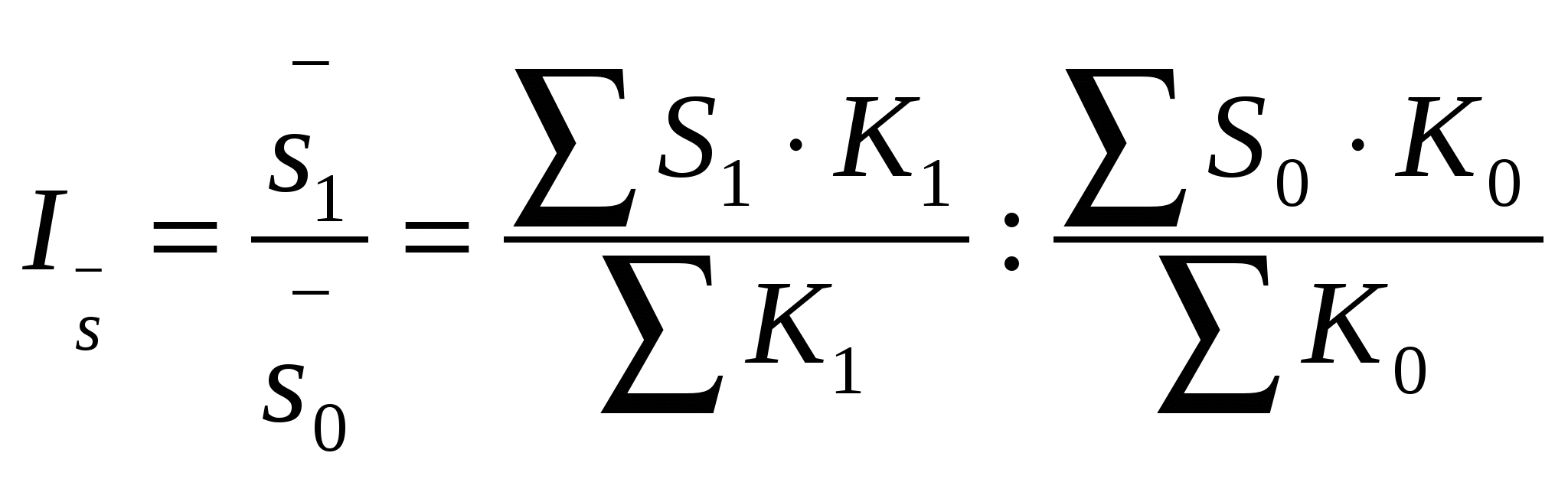 .В индекс переменного состава учитываются одновременно и влияние структурных изменений в составе совокупности, и изменение уровня качественного признака отдельных объектов. В этом смысле показанные ранее индексы, полученные по типу индекса цен:  ,являются индексами постоянного, или фиксированного, состава. Формула индекса структурных изменений для нашего примера:  , так как  и  .Таким образом, индекс переменного состава выражается произведением индекса структурных изменений на индекс постоянного состава:  24. Основы индексного факторного анализа. Методы разложения абсолютного прироста по факторам. статистике, планировании и анализе хозяйственной деятельности основой для количественной оценки роли отдельных факторов в динамике изменений обобщающих показателей являются индексные модели. Индексный метод – один из приемов элиминирования. Основывается на относительных показателях динамики, пространственных сравнений, выполнении плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому, или по другому объекту). Любой индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений – групповыми, или тотальными. Статистика оперирует различными формами индексов (агрегатная, арифметическая, гармоническая и др.), используемыми в аналитической работе. Агрегатный индекс является основной формой любого общего индекса; его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях. Корректность определения размера каждого фактора зависит от:
Принципы построения индексов: изменение одного фактора при неизменном значении всех остальных, при этом если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода. Пусть Y = а*b*с*d. Тогда:  При этом: I Y=I a*I b*I c*I d. Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя. В этом случае влияние отдельных факторов определяется с помощью разности между числителем и знаменателем соответствующих индексов, т. е. также при расчете влияния одного фактора элиминируется влияние другого: Пусть Y = а*b, где а – количественный фактор, a b – качественный. Тогда: a 1*b 0—a 0*b 0– абсолютный прирост результирующего показателя за счет фактора а; a 1*b 1—a 1*b 0– абсолютный прирост результирующего показателя за счет фактора b; a 1*b 1—a 0*b 0– абсолютный прирост результирующего показателя за счет влияния всех факторов. Данный принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой – качественный), а анализируемый показатель представлен как их произведение. Теория индексов не дает общего метода разложения абсолютных отклонений обобщающего показателя по факторам при числе факторов более двух. Для решения этой задачи используется метод цепных подстановок. 25. Территориальные индексы: понятие, способы расчета. Территориальные индексы – это разновидность относительных величин сравнения, сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, но к разным территориям (городам, районам, областям). На основе территориальных индексов выполняются международные сопоставления. Построение простейших территориальных индексов рассмотрим на примере показателя товарооборота для двух районов. Территориальный индекс товарооборота – это отношение суммы выручки от продажи в одном из районов (А) к аналогичному показателю в другом (Б).  .Различие объемов товарооборота вызвано различием ассортимента и количества проданных товаров, а также различием цен. Территориальный индекс физического объема товарооборота рассчитывается как 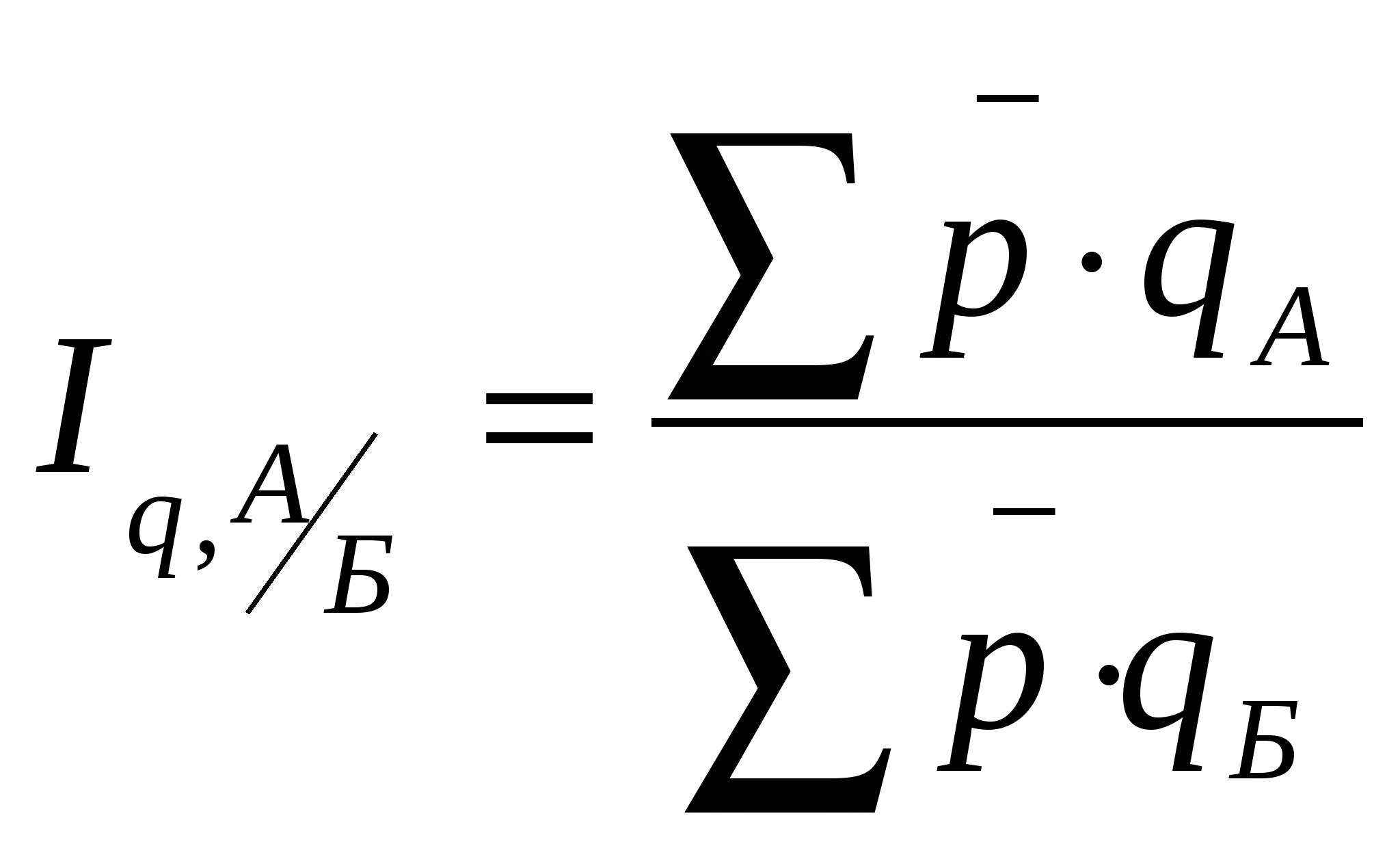 .Территориальный индекс цен  .В этих формулах  - средняя межрайонная цена товара каждого вида,   - суммарный по двум районам объем продаж каждого вида товара. 26. Макроэкономическая статистика: предмет, задачи, основные категории. Предметом изучения макроэкономической статистики является количественная характеристика массовых явлений и процессов в экономике страны с учетом их качественных различий. Макроэкономическая статистика решает следующие задачи: - информационное обеспечение разработки экономической политики правительства, оценки ее результатов, разработки различных государственных программ и мер по их реализации, составления экономических прогнозов; - информационное обеспечение двухсторонних и многосторонних экономических отношений; - информационное обеспечение предпринимательской деятельности, информирование о развитии экономики и социальной сферы руководителей предприятий и компаний, менеджеров производства и бизнесменов с целью лучшего понимания макроэкономического климата, в котором функционируют их предприятия; - информирование широких слоев общественности и научных кругов об основных итогах и тенденциях социально-экономического развития страны; - предоставление информации о состоянии и развитии экономики страны в международные экономические организации: ООН, МВФ, ВБ и другие. Международная экономическая практика использует две системы макроэкономических расчетов: - Баланс народного хозяйства (БНХ) – используется странами социалистической ориентации с централизованным планированием и командно-административной системой. - Система национальных счетов (СНС) – характерна для стран с рыночной экономикой. Представляет собой экономико-статистическую модель, которая отражает движение национального продукта и национального дохода, а также основные взаимосвязи в экономике. Основными категориями СНС являются: - продукты, услуги; - трансферты; - экономическая территория; - институциональная единица; - институциональный сектор; - резидент, нерезидент экономики; - корпорация, квазикорпорация, заведение. 27. Основные макроэкономические показатели, их взаимосвязь. Основные макроэкономические показатели:
Показатели взаимосвязаны между собой, что позволяет использовать эту взаимосвязь для расчетов: А. Валовой внутренний продукт (ВВП); Б. Потребление основного капитала (ПОК); В. Чистый внутрений продукт (ЧВП = А – Б); Г. Сальдо первичных доходов из-за границы; Д. Валовой национальный доход (ВНД = А + Г); Е. Чистый национальный доход (ЧНД = Д – Б); Ж. Сальдо текущих трансфертов, полученных из-за границы. З. Валовой национальный располагаемый доход (ВНРД = Д + Ж). И. Конечное потребление (КП). К. Валовое национальное сбережение (ВНС = З – И). |