Статистика понятие, ее предмет и метод, основные категории

• Название: Статистика понятие, ее предмет и метод, основные категории
• Анкор: Statistika.doc
• Дата: 26.04.2017
• Размер: 0.83 Mb.
• Имя файла: Statistika.doc
• Тип: Документы; #5726
• страница: 2 из 8

8. Виды дисперсий. Правило сложения дисперсий.

Виды дисперсий:

1. 
   Межгрупповая дисперсия – оценивает вариацию средних значений в каждой группе относительно общего среднего уровня:
   

,

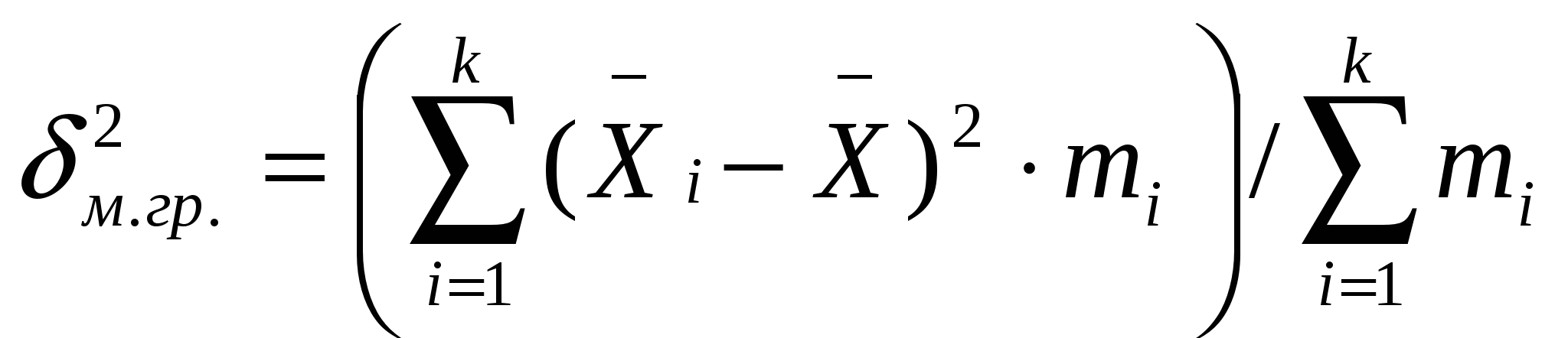где k – количество групп, на которые разбита вся совокупность;

m_i – количество объектов, наблюдений, включенных в группу i;

- среднее значение признака по группе i;

- общее среднее значение признака.

2. 
   Внутригрупповая
   

.

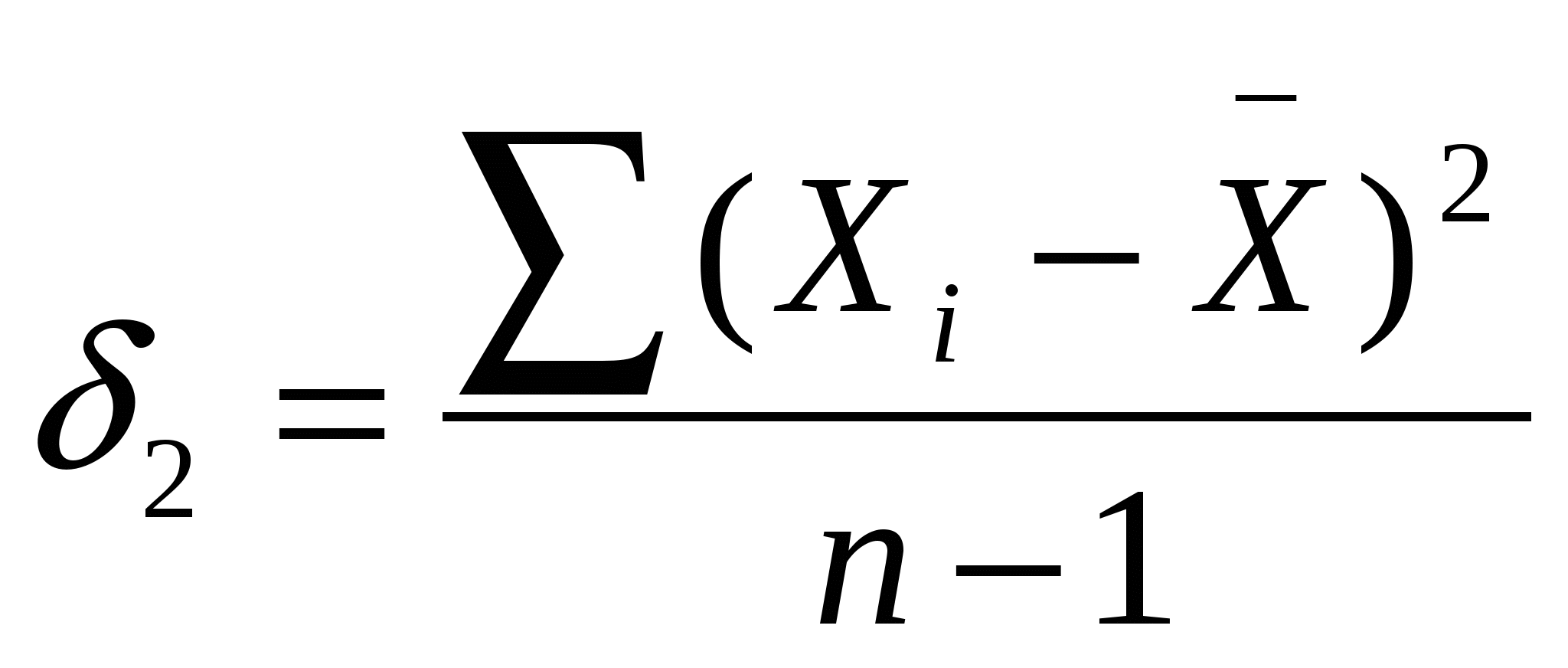Если первичные данные по признаку Х разделить на группы, то дисперсия признака может быть определена как традиционным способом по первичным данным , так и как сумма межгрупповой дисперсии и средней величины внутригрупповых. Среднее значение внутригрупповых дисперсий рассчитывается по формул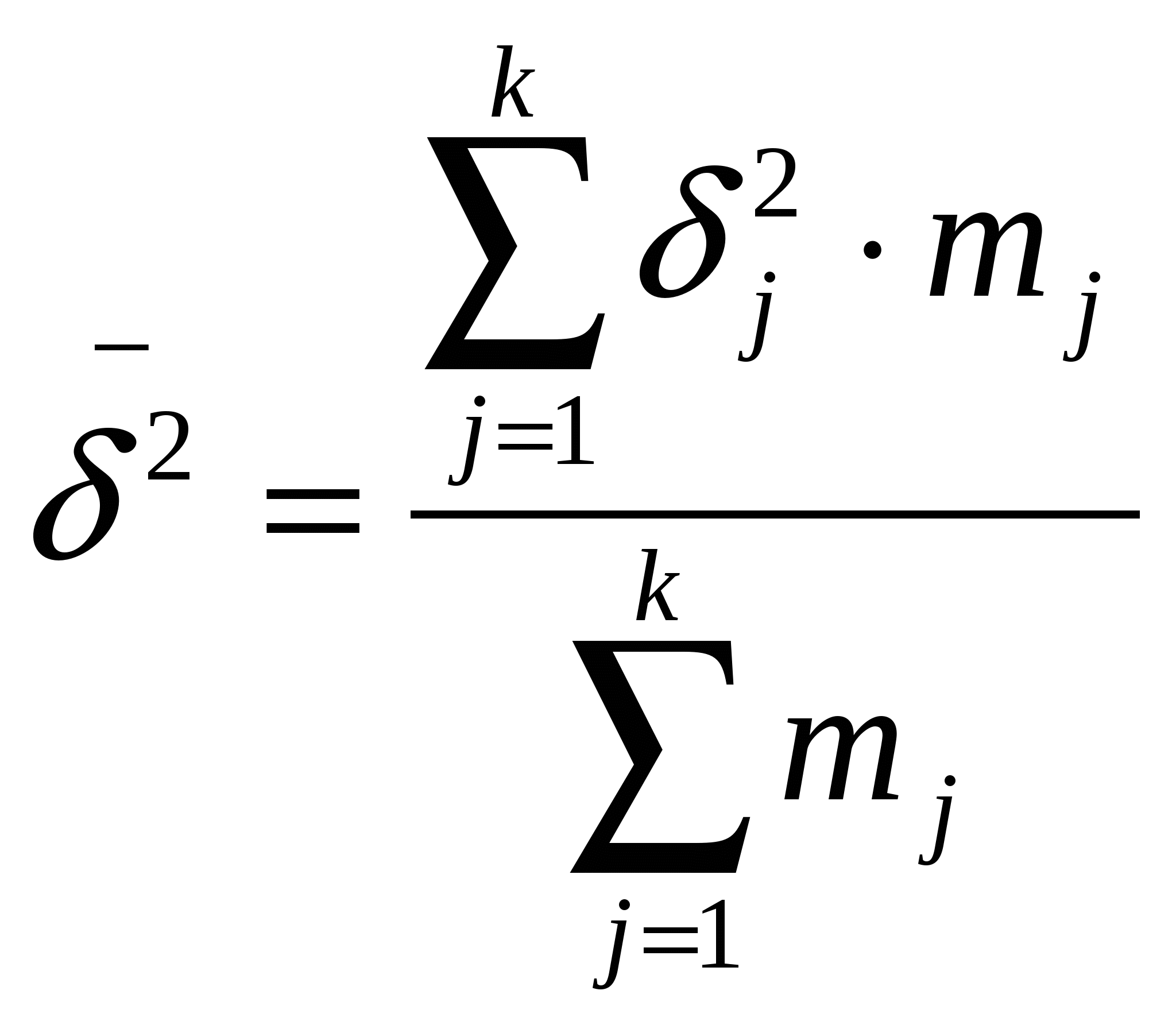е:

; где .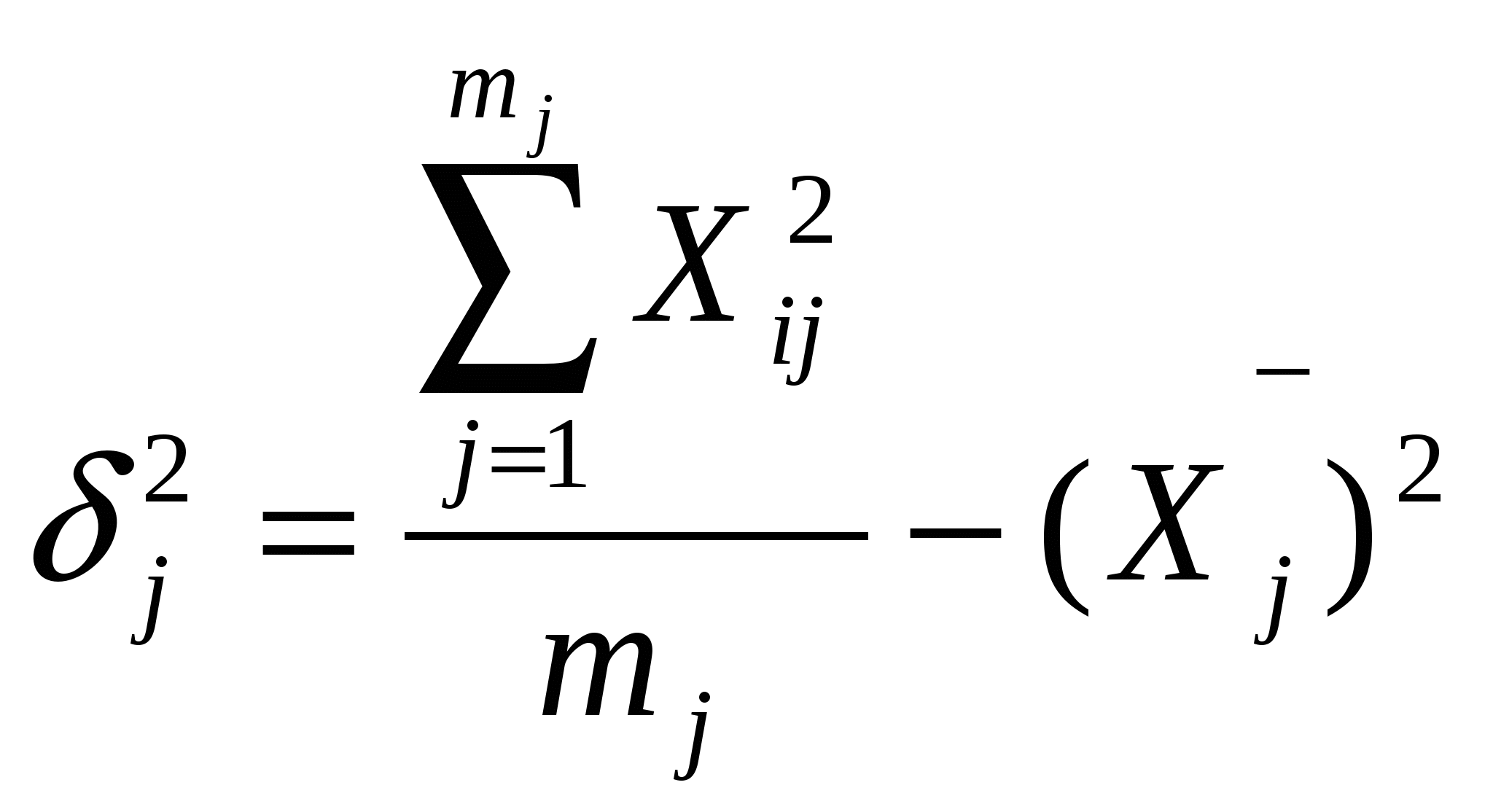

9. Выборочный метод как основной вид несплошного статистического наблюдения. Виды, методы и способы отбора, обеспечивающие репрезентативность выборки.

Выборочный метод применяется, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. Единицы, которые отобраны для наблюдения, принято называть выборочной совокупностью, а всю совокупность, из которой производится отбор, - генеральной. Качество выборочного наблюдения зависит от того, насколько выборка репрезентативна, т.е. насколько состав выборки представляет генеральную совокупность. Для репрезентативности необходимо соблюдение принципа случайности отбора единиц.

Способы формирования выборочной совокупности:

1. 
   Случайный отбор, осуществляется с помощью жеребьевки либо по таблице случайных чисел.
   
2. 
   Механический отбор – отбирается каждый n-й элемент генеральной совокупности.
   
3. 
   Стратифицированный отбор – используется для отбора единиц из неоднородной совокупности.
   
4. 
   Серийный (гнездовой) отбор – это такая форма отбора, при которой в случайном или механическом порядке выбирают не единицы, а определенные районы, серии (гнезда), внутри которых производится сплошное наблюдение.
   

Особенности обследуемых объектов определяют две методики отбора единиц – повторная и бесповторная. При повтором отборе каждая попавшая в выборку единица или серия возвращается в генеральную совокупность и может попасть в выборку вторично. При этом вероятность попадания в выборочную совокупность всех единиц генеральной совокупности остается одинаковой. Бесповторный отбор означает, что каждая отобранная единица в генеральную совокупность не возвращается.
10. Ошибки выборочного наблюдения, понятие, виды, способы расчета. Распространение данных выборочного наблюдения на генеральную совокупность.

Разность между показателями в выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности. Ошибки регистрации возникают из-за неправильных или неточных сведений. Среди ошибок регистрации выделяются систематические, обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (округление цифр), и случайные, проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.

Ошибки репрезентативности также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки – принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между характеристиками выборочной и генеральной совокупности.

Выборочная средняя и выборочная доля являются величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Размер их отклонений от генеральных значений случаен и оценивается посредством так называемой средней(μ) и предельной ошибки выборки (Р).

Распространение выборочных оценок на генеральную совокупность состоит в определении характеристик генеральной совокупности на основе характеристик выборочной. Применяются два способа распространения выборочных данных:

1. 
   способ прямого пересчета;
   
2. 
   способ поправочных коэффициентов.
   

11. Статистические методы изучения взаимосвязей. Меры тесноты взаимосвязи.

Для изучения взаимосвязей в статистике используются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. Иногда эти методы объединяют в один корреляционно-регресионный анализ (КРА).

Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причин связей и оценке факторов, оказывающих наибольшее влияние на вариацию результативного признака. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования управления для оценки неизвестных значений зависимой переменной.

Методы оценки тесноты связи распределяются на параметрические (корреляционные) и непараметрические. Параметрические методы основаны на использовании оценок параметров распределения вероятностей изучаемых величин: математического ожидания, дисперсии и т.д.

Непараметрические методы применяют для оценки связи атрибутивных (качественных) признаков и для оценки корреляционных связей.

12.​ Этапы корреляционно–регрессионного анализа. Расчет параметров уравнения регрессии, их экономический смысл.

Дли изучения взаимосвязи в статистике используются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. Иногда эти методы объединяют в один корреляционно-регрессионный анализ (КРА), что имеет под собой определенные основания: наличие целого ряда общих вычислительных процедур,

Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на вариацию результативного признака. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.

Методы анализа корреляции и регрессии широко представлены в современных системах обработки статистических данных на ПЭВМ (например, STATISTICA, SPSS). Исследователь должен подготовить исходную информацию и быть готовым к интерпретации полученных результатов. В настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов является обязательным условием исследования.

Методы оценки тесноты связи разделяются на параметрические (корреляционные) и непараметрические. Параметрические методы основаны на использовании оценок параметров распределения вероятностей изучаемых величин: математического ожидания, дисперсии и т.д., и, следовательно, применяются в случаях, когда эти параметры можно предварительно вычислить. На практике в начале исследования обычно считают, что первичные данные подчиняются закону нормального распределения вероятностей.

Непараметрическиеметоды не накладывают ограничений на закон распределения изучаемых величин и обычно более просты в вычислениях. Поэтому их применяют и для оценки корреляционных связей, и особенно широко для оценки связи атрибутивных (качественных) признаков.
7.2. Парная корреляция и парная линейная регрессия
Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы. В основу таблицы положена группировка двух изучаемых во взаимосвязи признаков – X и Y. Частоты f_ij показывают количество соответствующих сочетаний X и Y. Если f_ij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания f_ij допустимо утверждать о связи между X и Y. При этом, если f_ij концентрируются около одной из двух диагоналей, имеет место прямая или обратная линейная связь.

Уровни признака X	Уровни признака Y
	Y1	Y2	…	Ym	Итого
X1	f11	f12	…	f1m
X2	f21	f22	…	f2m
…	…	…	…	…	…	…
Xk	fk1	fk2	…	fkm
Всего			…		n
			…			–

Рисунок 7.1. Схема корреляционной таблицы
Наглядным отображением корреляционной таблицы служит корреляционное поле. Оно представляет график, где на оси абсцисс откладываются значения X, по оси ординат – Y, а точками показывается сочетание первичных наблюдений X и Y. По расположению точек, их концентрации в определенном направлении можно судить о наличии и форме связи.

В итогах корреляционной таблицы по строкам и столбцам приводятся два распределения – одно по X, другое по Y. Рассчитаем для каждого X_i среднее значение Y и для Y_jсреднее значение X.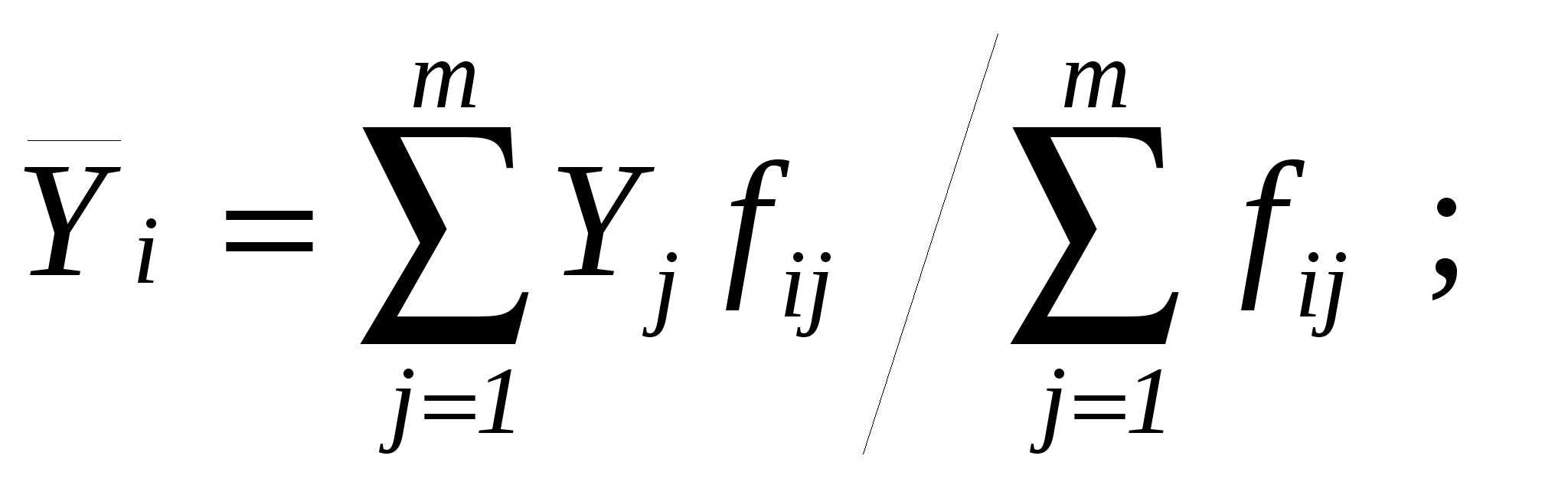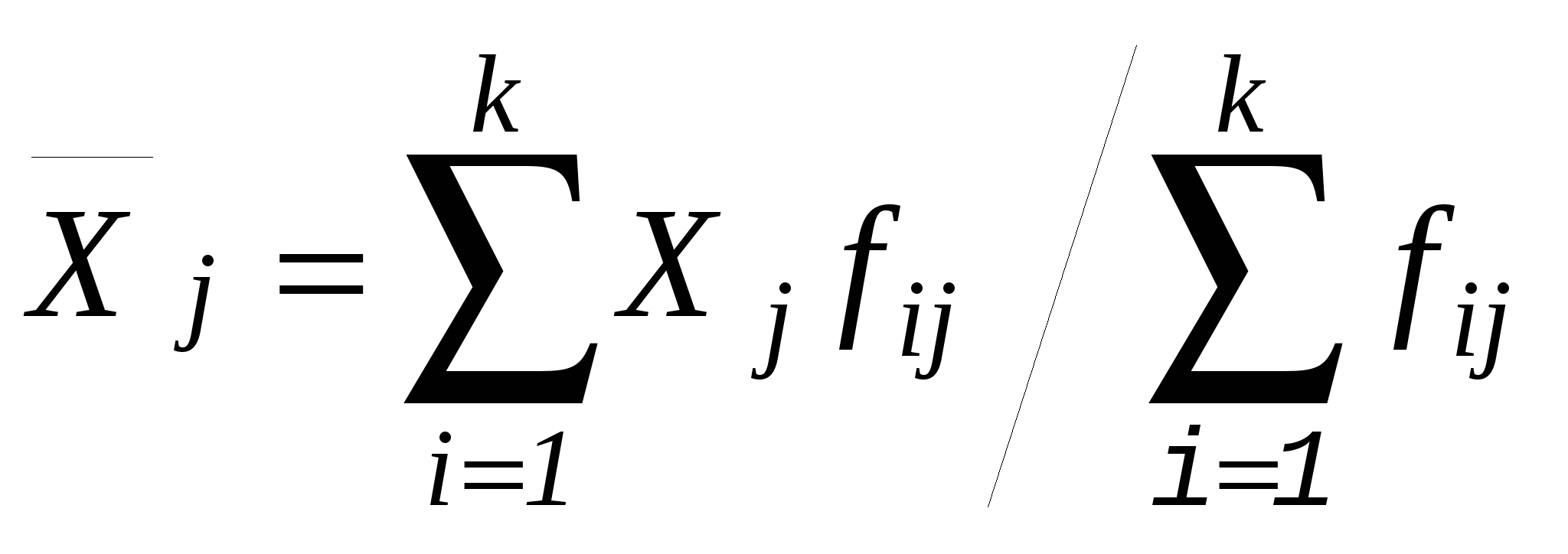

; i = 1, 2, …, k; j = 1, 2, …, m.

Последовательность точек на графике иллюстрирует зависимость среднего значения результативного признака Y от факторного X; соединяя точки линиями, получаем эмпирическую линию регрессии, наглядно показывающую, как изменяется Y по мере изменения X. Аналогичным образом, последовательность точек на графике иллюстрирует зависимость среднего значения факторного признака X от результативного Y; соединяя точки линиями, также получаем эмпирическую линию регрессии, наглядно показывающую, как изменяется X по мере изменения Y. Таким образом, на одном графическом поле можно расположить две линии регрессии
13.​ Понятие о множественной регрессии и корреляции. Меры тесноты связей в многофакторной системе.
Множественная корреляция
Если имеется система статистических показателей: Y, X₁, X₂, …, X_m, то представляет интерес оценка корреляции между всеми парами показателей этой системы. Все парные коэффициенты корреляции могут быть представлены в одной квадратной матрице R размерностью (m+1)×(m+1), котораяназывается матрицей парных линейных коэффициентов корреляции. На основе матрицей R, можно определить так называемые коэффициенты множественной линейной корреляции признаков и коэффициенты парной линейной частной корреляции.

Коэффициент множественной линейной корреляции оценивает степень линейной связи одного из признаков системы с совокупностью прочих признаков этой же системы. В общем случае для измерения множественной линейной корреляции определяются параметры множественного уравнения регрессии и теоретические уровни признака-результата (например,Y). На основе фактических и рассчитанных по уравнению (теоретических) значений признака Y вычисляется коэффициент множественной корреляции R_y: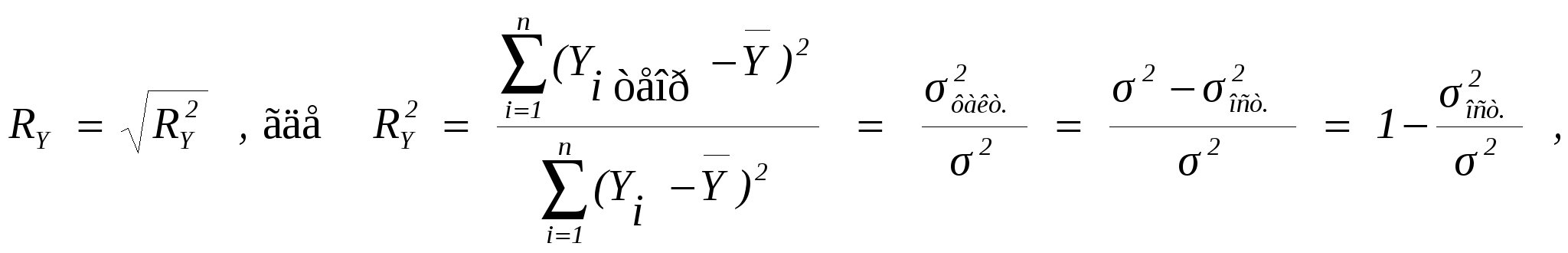



где ² – общая (фактическая) дисперсия уровней результативного признака (дисперсия Y); σ²_факт.– факторная дисперсия или дисперсия теоретических значений признака результата относительно среднего уровня; σ²_ост.– остаточная дисперсия, характеризующая вариацию Y за счет факторов, не учтенных уравнением регрессии. Известно, что общая дисперсия признака результата Yскладывается из факторной и остаточной составляющих.

Коэффициент множественной корреляции изменяется от 0 до 1. Чем ближе R_Y к 1, тем более сильная связь между Y и множеством X. Если коэффициент R_Y незначителен по величине (как правило, R_Y0,3), то можно утверждать, что или не все важнейшие факторы взаимосвязи учтены, или выбрана неподходящая форма уравнения. В последнем случае пересматривается список переменных модели и возможно, её вид.

Для нелинейной множественной связи рассчитывают индекс корреляции. Методика его вычисления аналогична, но взаимодействие факторов и функция регрессии рассматриваются как нелинейные. Индекс корреляции изменяется в пределах от 0 до 1. Квадрат R равен так называемому коэффициенту детерминации (D или R²). Он показывает, какая часть вариации зависимого признака объясняется включенными в модель факторов.

Показатели множественной корреляции рассчитываются по приведенной выше схеме не часто. Если признак-результат Y включен в общую систему признаков, то на основе общей матрицы парных линейных коэффициентов R можно получить всю совокупность коэффициентов множественной корреляции, так как любой из признаков этой системы может, в принципе, претендовать на роль признака-результата. Коэффициент множественной корреляции, оценивающий степень линейной зависимости любого признака j от всех прочих в этой системе, определяется по формуле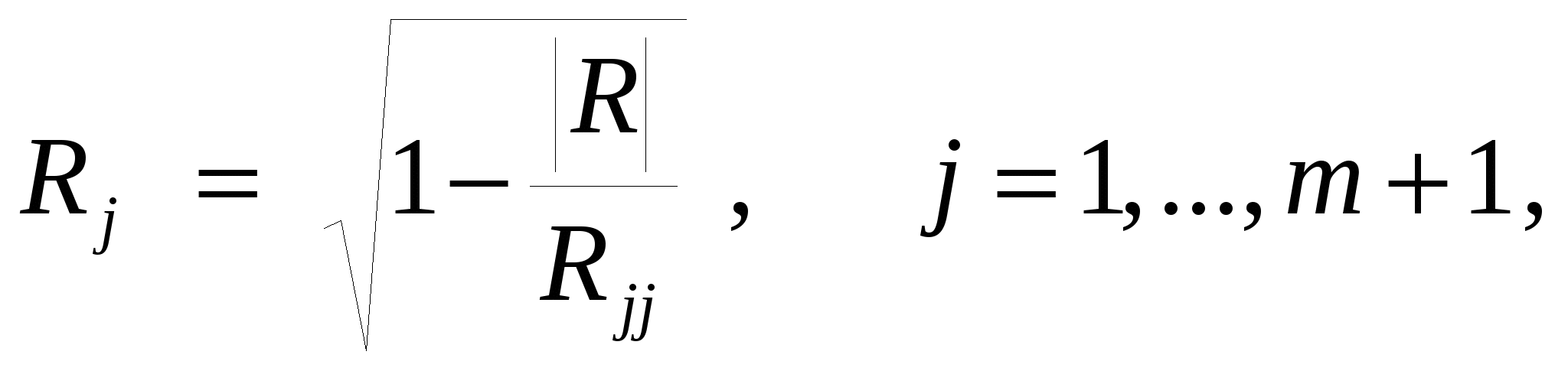



где (m+1) – число всех признаков в системе; |R| –определитель матрицы R парных линейных коэффициентов корреляции; R_ii – алгебраическое дополнение элемента (jj) для этой же матрицы.