Статистика. Статистика Предмет и задачи статистики
 Скачать 1.24 Mb.
|
|
Способы распространения характеристик выборки на генеральную совокупность. Выборочный метод чаще всего применяется для получения характеристик генеральной совокупности по соответствующим показателям выборки. В зависимости от целей исследований это осуществляется или прямым пересчётом показателей выборки для генеральной совокупности, или посредством расчёта поправочных коэффициентов. Способ прямого пересчёта. Он состоит в том, что показатели выборочной доли  или средней  распространяется на генеральную совокупность с учётом ошибки выборки.Так, в торговле определяется количество поступивших в партии товара нестандартных изделий. Для этого (с учётом принятой степени вероятности) показатели доли нестандартных изделий в выборке умножаются на численность изделий во всей партии товара. Способ поправочных коэффициентов. Применяется в случаях, когда целью выборочного метода является уточнение результатов сплошного учета. В статистической практике этот способ используется при уточнении данных ежегодных переписей скота, находящегося у населения. Для этого после обобщения данных сплошного учета практикуется 10%-ное выборочное обследование с определением так называемого “процента недоучета”. Способы отбора единиц из генеральной совокупности. В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения. Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности. Существуют следующие способы отбора единиц из генеральной совокупности: 1) индивидуальный отбор — в выборку отбираются отдельные единицы; 2) групповой отбор — в выборку попадают качественно однородные группы или серии изучаемых единиц; 3) комбинированный отбор — это комбинация индивидуального и группового отбора. Способы отбора определяются правилами формирования выборочной совокупности. Выборка может быть: — собственно-случайная; — механическая; — типическая; — серийная; — комбинированная. Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.  .Так, при 5%-ной выборке из партии товара в 2 000 ед. численность выборки n составляет 100 ед. (5*2000:100), а при 20%-ной выборке она составит 400 ед. (20*2000:100) и т.д. Механическая выборка состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица. Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осуществить, не прибегая к составлению списков. На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или поточной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т.д. Типическая выборка. При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность. Для определения средней ошибки типической выборки используются формулы: повторный отбор  ,  бесповторный отбор 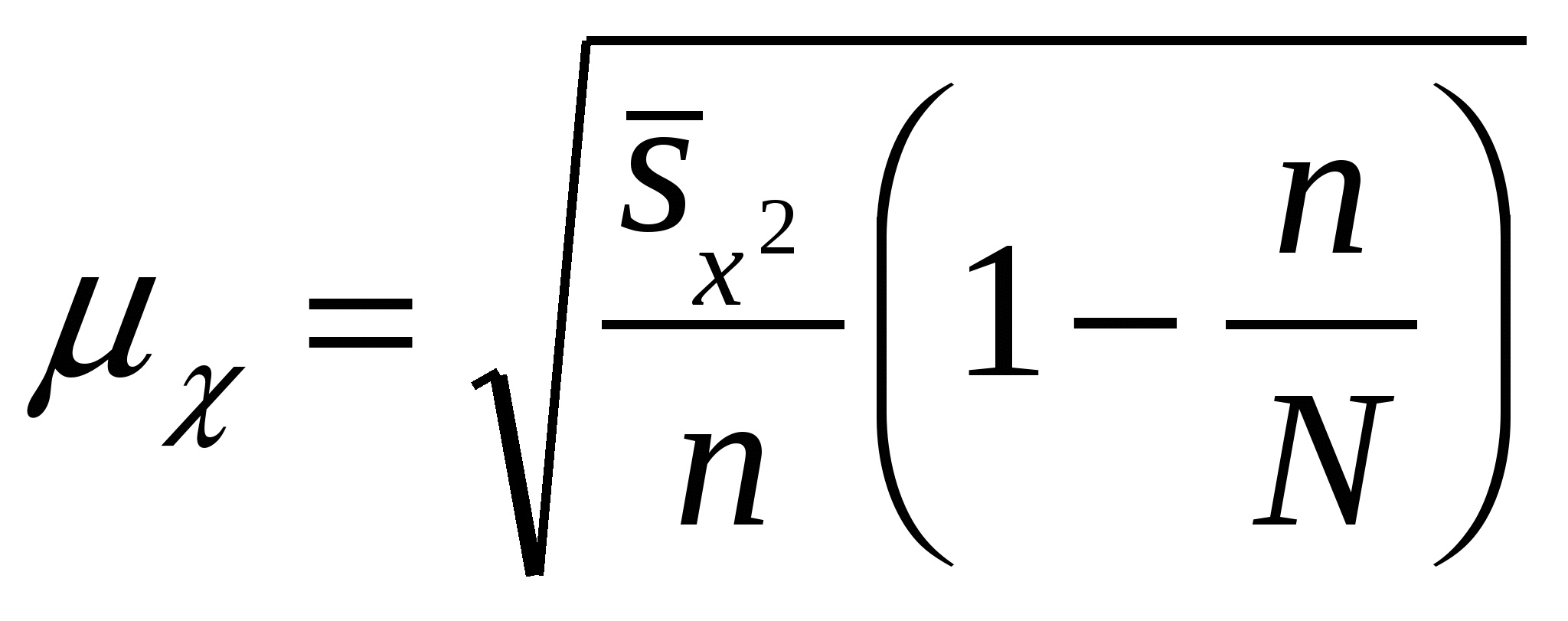 ,  Дисперсия определяется по следующим формулам:  ,  При одноступенчатой выборке каждая отобранная единица сразу же подвергается изучению по заданному признаку. Так обстоит дело при собственно-случайной и серийной выборке. При многоступенчатой выборке производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы. Так производится типическая выборка с механическим способом отбора единиц в выборочную совокупность. Комбинированная выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц. 17. Средняя и предельная ошибки выборки. Расчет доверительного интервала. ОПРЕДЕЛЕНИЕ ОШИБКИ ВЫБОРКИ Ошибка выборки — это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования. Определение ошибки выборочной средней. При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:  где  — средняя ошибка выборочной средней; — дисперсия выборочной совокупности;n — численность выборки. При бесповторном отборе она рассчитывается по формуле:  где N — численность генеральной совокупности. Определение ошибки выборочной доли. При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:  где  — выборочная доля единиц, обладающих изучаемым признаком; — число единиц, обладающих изучаемым признаком;  — численность выборки.При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:  Предельная ошибка выборки  связана со средней ошибкой выборки отношением:  При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки. Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам: 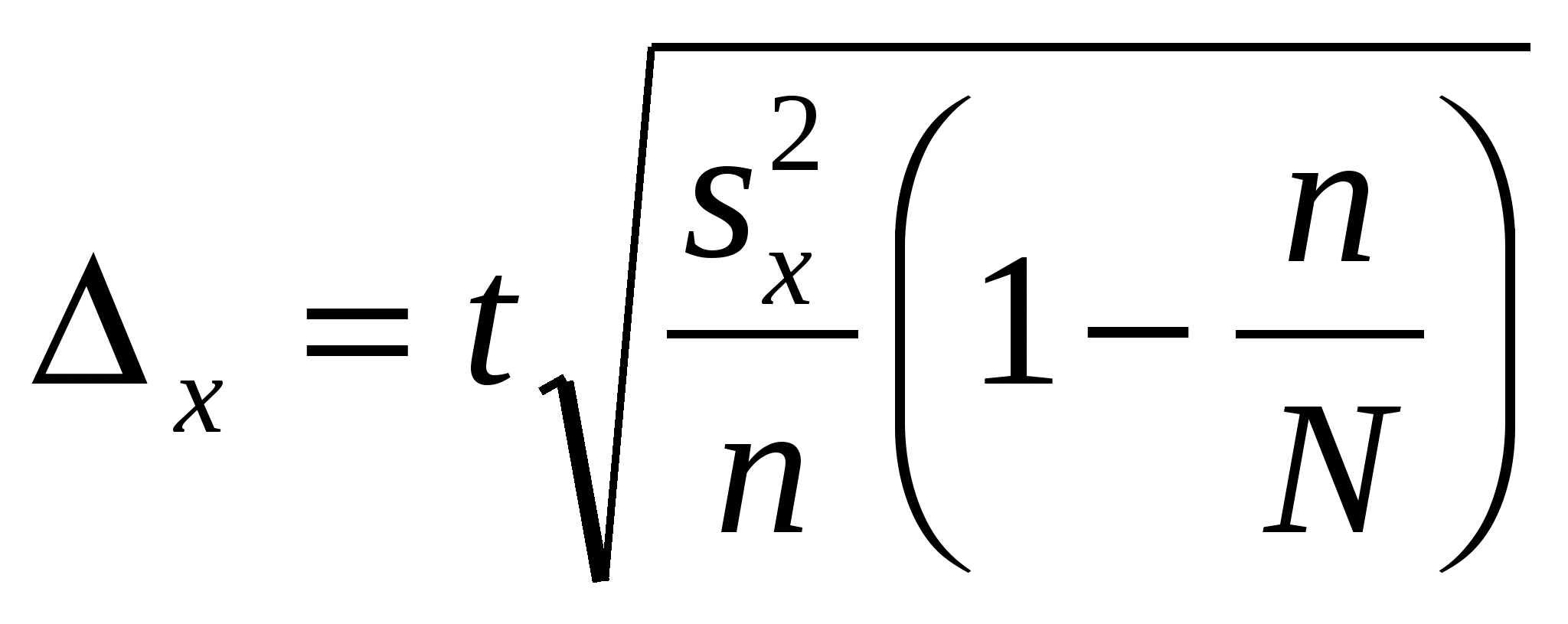  Предельная ошибка выборки при повторном отборе определяется по формуле:   18. Расчет необходимой численности выборки, обеспечивающей с определенной вероятностью заданную точность наблюдения. Смотри 17 ответ. Трудовые и материальные затраты на проведение выборки напрямую зависят от ее численности, поэтому чрезвычайно важно до оптимума сохранить численность выборки, так чтобы не утратить ее точность. Поиск оптимальной численности выборки удобно осуществлять на основе формул средней и предельной ошибок. Из формулы средней ошибки случайного повторного отбора видно, что величина средней ошибки обратно пропорциональна квадратному корню из численности выборки ([pic]). Чтобы сократить среднюю ошибку в 2 раза, нужно численность выборки увеличить в 4 раза. Используя формулу предельной ошибки выборки [pic] можно найти численность [pic]. Это оптимальная численность выборки для случайного повторного отбора. Пример: Для определения среднего размера банковского вклада сроком на 91 день необходимо провести повторный отбор из совокупности в 2500 договоров. Какое количество договоров необходимо отобрать, чтобы с вероятностью 0,954 предельная ошибка выборки не превысила 25 руб. N=2500 p=0,954 (=25 руб. n-? (2=8900 Расчет численности выборки основывается на статистическом подходе обработки данных и за ним стоит множество вычислений, но для простоты, ниже мы представим формулу, следуя которой можно достичь хороших результатов. 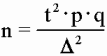 n – Количество элементов в выборке. t – Определяется по таблице значений функции F(t), при условии известной исследователю доверительной вероятности. Практически всегда не больше 3. 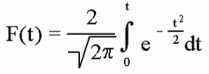 p – Доля брака в генеральной совокупности. q – Доля качественной продукции в генеральной совокупности. Если соотношение брака и качественной продукции не известно, то положим p=0,5 и q=0,5 . Δ – Заданная точность. Пример 1. Пусть необходимо определить объем выборки, которая позволила бы оценить долю брака в партии продукции (10000 единиц) с точностью до 2% при доверительной вероятности P = 0,95. То есть, если истинная доля брака составляет k%, то с вероятностью 0,95 мы хотим получить долю брака k’% лежащую в интервале k% + 2% < k’% < k% - 2%. Численность выборки может быть определена по формуле  Где при неизвестных p и q положим их равными 0,5. Δ = 0,02, значение t определяется по таблице (смотрите ниже), по заданной доверительной вероятности и равно 2. Таблица значений функции Лапласа:   Однако это число можно и уменьшить, например используя дополнительную информацию. Допустим нам известно приблизительное значение p=0,1, тогда q=1-p=0,9 и используя эти цифры получаем:  Каким способом следует выбирать данные? Для того чтобы посредством выборки как можно лучше оценить генеральную совокупность, выборка должна иметь каждое свойство генеральной совокупности. Выборка называется репрезентативной, если каждое свойство в выборке и в генеральной совокупности имеет одинаковые частоты. Выборка имеет больше шансов быть репрезентативной, если она построена таким образом, что (1) каждые объект генеральной совокупности имеет одинаковую вероятность быть отобранным и (2) объекты отбираются независимо друг от друга. Есть несколько методов извлечения выборки: применение таблиц случайных чисел, метод перемешивания генеральной совокупности, стратифицированная случайная выборка, систематическая выборка. Ниже мы рассмотрим первые два из этих методов. 1. Применение таблицы случайных чисел. Одним из способов извлечения случайной выборки является применение таблицы случайных чисел. Определение: Таблица случайных чисел – это набор цифр такой, что вероятность возникновения любой цифры от 0 до 9 одна и та же. 2057 0762 1429 8535 9029 9745 3458 5023 3502 2436 6435 2646 0295 6177 2755 3080 3275 0521 6623 1133 3278 0500 7573 7426 3188 0187 7707 3047 4901 3519 7888 6411 1631 6981 1972 4269 0022 3860 1580 6751 4022 6540 7804 5528 4690 3586 9839 6641 0404 0735 0888 3504 2651 9051 5764 7155 6489 2660 3341 8784 … 19. Ряды динамики: понятие, виды (моментные, интервальные). Показатели ряда динамики. РЯДЫ ДИНАМИКИ. КЛАССИФИКАЦИЯ. Рядами динамики наз. стат. данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных эл-та: показатель времени t; соответствующие им уровни развития изучаемого явления у. В кач-ве показаний времени в рядах динамики выступают либо опр. даты времени, либо отдельные периоды. Уровни рядов динамики отображают колич-ную оценку развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами. В зависимости от хар-ра изучаемого явления уровни рядов динамики могут относиться или к опр. датам, или к отдельным периодам. В соответствии с этим, ряды динамики делятся на моментные и интервальные. Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть персонала фирмы N, составляющая списочную численность на 1.01.1994г., продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет. Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени. Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а сумма товарооборота четырех кварталов дает объем товарооборота за год и т.д. Ряды динамики могут быть полными и неполными. Полный - в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга. Неполный - в котором уровни зафиксированы в неравноотстоящие моменты. Чтобы анализ ряда был объективен, необходимо учитывать события, приводящие к несопоставимости уровней ряда и использовать приемы приведения рядов в сопоставимый вид. Наиболее характерные случаи несопоставимости уровней ряда динамики: Территориальные изменения объекта исследования, к которому относится изучаемый показатель. Разновеликие интервалы времени, к которым относится показатель. Изменение даты учета. Изменение методологии учета или расчета показателя. Изменение цен. Изменение единиц измерения. 1982 1983 1984 22,0 22,3 22,8 - в старых границах района. 1985 1986 1987 34,2 34,3 34,4 - в новых границах района. Для приведения ряда в сопоставимый вид необходимо для 1984 года знать численность населения в старых и новых границах района для определения коэфф. пересчета: К=34,2/22,8=1,5 Все уровни ряда до 1984 года, умножаются на коэфф. К и ряд принимает вид: 1982 1983 1984 1985 1986 1987 33,0 33,3 34,2 34,2 34,3 34,4 После этого преобразования ряда динамики возможен дальнейший анализ ряда. В качестве обобщенной характеристики уровней ряда динамики служит средний уровень ряда динамики. В зависимости от типа ряда динамики используются различные расчетные формулы. Интервальный ряд абсолютных величин с равными периодами (интервалами времени): 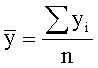 . 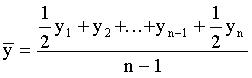Моментный ряд с равными интервалами между датами:  . Моментный ряд с неравными интервалами между датами: 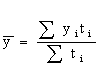 . где yi - уровни ряда, ПОКАЗАТЕЛИ АНАЛИЗА РЯДОВ ДИНАМИКИОдним из важнейших направлений анализа рядов динамики явл. изучение особенностей развития явления за отдельные периоды времени. Для динамических рядов рассчитывают ряд показателей: К - темпы роста; y- абсолютные приросты;K- темпы прироста. Темп роста - относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем: 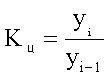 , либо как базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем y0, выбранным за базу сравнения:  . Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов. Абсолютный прирост - разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть цепными и базисными, в зависимости от способа выбора базы для сравнения:цепной абсолютный прирост -  ; базисный абсолютный прирост - . Для относительной оценки абсолютных приростов рассчитываются показатели темпов прироста. Темп прироста - относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения. Базисные и цепные темпы прирос:  . yб и yц- абсолютный базисный или цепной прирост; y0- уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов; yi-1 - уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.Существует связь между темпами роста и прироста: К = К - 1 или К = К - 100 % (если темпы роста определены в процентах). Если разделить абсолютный прирост (цепной) на темп прироста (цепной) за соответствующий период, получим показатель, называемый - абсолютное значение одного процента прироста:  .По показателям изменения уровней ряда динамики (абсолютные приросты, темпы роста и прироста), полученным в результате анализа исходного ряда, могут быть рассчитаны обобщающие показатели в виде средних величин - средний абсолютный прирост, средний темп роста, средний темп прироста. Средний абсолютный прирост может быть получен по одной из формул: 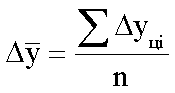 или ,где n - число уровней ряда динамики;y1 - первый уровень ряда динамики; yn- последний уровень ряда динамики;yцi- цепные абсолютные приросты. Средний темп роста можно определить, пользуясь формулами: 20. Средние показатели ряда динамики. В качестве обобщенной характеристики уровней ряда динамики служит средний уровень ряда динамики  . В зависимости от типа ряда динамики используются различные расчетные формулы.Интервальный ряд абсолютных величин с равными периодами (интервалами времени):  Моментный ряд с равными интервалами между датами:  Моментный ряд с неравными интервалами между датами:  где  - уровни ряда, сохраняющиеся без изменения на протяжении интервала времени  .21.Методы сглаживания рядов динамики. Методы сглаживания и выравнивания динамических рядов. Исключение случайных колебаний значений уровней ряда осуществляется с помощью нахождения «усредненных» значений. Способы устранения случайных факторов делятся на две больше группы: 1. Способы «механического» сглаживания колебаний путем усреднения значений ряда относительно других, расположенных рядом, уровней ряда. 2. Способы «аналитического» выравнивания, т. е. определения сначала функционального выражения тенденции ряда, а затем новых, расчетных значений ряда. 1.2. 1 Методы «механического» сглаживания. Сюда относятся: а. Метод усреднения по двум половинам ряда, когда ряд делится на две части. Затем, рассчитываются два значения средних уровней ряда, по которым графически определяется тенденция ряда. Очевидно, что такой тренд не достаточно полно отражает основную закономерность развития явления. б. Метод укрупнения интервалов, при котором производится увеличение протяженности временных промежутков, и рассчитываются новые значения уровней ряда. в. Метод скользящей средней. Данный метод применяется для характеристики тенденции развития исследуемой статистической совокупности и основан на расчете средних уровней ряда за определенный период. Последовательность определения скользящей средней:
y1 = y1/m, где y1 – I-ый уровень ряда; m – членность скользящей средней.
Отрицательной стороной использования метода скользящей средней является образование сдвигов в колебаниях уровней ряда, обусловленных «скольжением» интервалов укрупнения. Сглаживание с помощью скользящей средней может привести к появлению «обратных» колебаний, когда выпуклая «волна» заменяется на вогнутую. В последнее время стала рассчитываться адаптивная скользящая средняя. Ее отличие состоит в том, что среднее значение признака, рассчитываемое также как описано выше, относится не к середине ряда, а к последнему промежутку времени в интервале укрупнения. Причем предполагается, что адаптивная средняя зависит от предыдущего уровня в меньшей степени, чем от текущего. То есть., чем больше промежутков времени между уровнем ряда и средним значением, тем меньшее влияние оказывает значение этого уровня ряда на величину средней. г. Метод экспоненциальной средней. Экспоненциальная средняя – это адаптивная скользящая средняя, рассчитанная с применением весов, зависящих от степени «удаленности» отдельных уровней ряда от среднего значения. Величина веса убывает по мере удаления уровня по хронологической прямой от среднего значения в соответствии с экспоненциальной функцией, поэтому такая средняя называется экспоненциальной. На практике применяется многократное экспоненциальное сглаживания ряда динамики, которое используется для прогнозирования развития явления. Вывод: способы, включенные в первую группу, ввиду применяемых методик расчета предоставляют исследователю очень упрощенное, неточное, представление о тенденции в ряду динамики. Однако корректное применение этих способов требует от исследователя глубины знаний о динамике различных социально - экономических явлений. 1.2.2 Методы «аналитического» выравнивания Более точным способом отображения тенденции динамического ряда является аналитическое выравнивание, т. е. выравнивание с помощью аналитических формул. В этом случае динамический ряд выражается в виде функции у (t), в которой в качестве основного фактора принимается время t, и изменения аргумента функции определяют расчетные значения уt. Фактическими (или эмпирическими) уровнями ряда динамики называют исходные данные об изменении явления, т. е. данные, полученные опытным путем, посредством наблюдения. Они обозначаются уi. Расчетными (или теоретическими) уровнями ряда называют значения, полученные в результате подстановки в уравнение тренда значений t, и обозначают их. Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t) . На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t) , а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом , чтобы она давала содержательное объяснение изучаемого процесса . Чаще всего при выравнивании используются следующий зависимости : линейная  ;параболическая  ;экспоненциальная  или  ).1)Линейная зависимость выбирается в тех случаях , когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные и цепные приросты , не проявляющие тенденции ни к увеличению , ни к снижению. 2)Параболическая зависимость используется , если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития , но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют . 3)Экспоненциальные зависимости применяются , если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста , темпов прироста , коэффициентов роста) , либо , при отсутствии такого постоянства , -- устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста , цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.д.) Таким образом, целью аналитического выравнивания является: - определение вида функционального уравнения; - нахождения параметров уравнения; - расчет «теоретических», выровненных уровней, отображающих основную тенденцию ряда динамики. Графическое отображение изменения уровней ряда играет большую роль в применении данного вида выравнивания. Оно позволяет ускорить процедуру анализа и увеличить степень наглядности полученных результатов. Сезонность – изменения динамических рядов, имеющих внутригодичную цикличность, зависящие от календарного периода года, явлениями природы, праздниками и др. Например, объем продаж продукции меховой фабрики вырастет в октябре, в ноябре достигнет максимума, снизится к марту, и затем до сентября - октября будет держаться на очень низком уровне. В качестве примера, интересно сравнить сезонные изменения уровня цен в России и странах Западной Европы. В России уровень цен в предпраздничные дни (например, рождество, Новый год, 9 мая, 1 сентября и т. д.) заметно растет. Тогда как в Западной Европе, как правило, в предпраздничные дни проводятся распродажи, т. е. в большинстве своем цены падают. Явления, подверженные сезонным изменениям, необходимо исследовать на предмет наличия основной тенденции развития. Для этого необходимо распределить объем изменения явления между сезонной составляющей и основной тенденцией. Изучение и измерение сезонности ряда динамики осуществляется с помощью специального показателя – индекса сезонности . Существует несколько вариантов анализа динамики с помощью индекса сезонности. Индексы сезонности показывают , во сколько раз фактический уровень ряда в момент или интервал времени t больше среднего уровня либо уровня , вычисляемого по уравнению тенденции f(t) . При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет . Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов каждого года . Индексы сезонности – это , по либо уровень существу , относительные величины координации , когда за базу сравнения принят либо средний уровень ряда , либо уровень тенденции . Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции . Если тренда нет или он незначителен , то для каждого месяца (квартала) индекс рассчитывается по формуле 32: 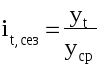 где  -- уровень показателя за месяц (квартал) t ; -- общий уровень показателя .Как отмечалось выше , для обеспечения устойчивости показателей можно взять больший промежуток времени . В этом случае расчет производится по формулам 33 : 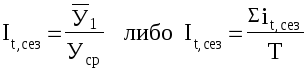 где  -- средний уровень показателя по одноименным месяцам за ряд лет ;Т -- число лет . При наличии тренда индекс сезонности определяется на основе методов , исключающих влияние тенденции . Порядок расчета следующий :
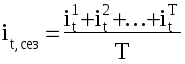 ,(Т -- число лет). Сглаживание рядов с помощью скользящей средней. Имеются данные о грузообороте предприятий транспорта РФ за 1999 г. , млрд. т. км.:
|
;