средние величины статистика. тема 26 Средние величины 2023. Статистики 5 Статистические

• Название: Статистики 5 Статистические
• Анкор: средние величины статистика
• Дата: 17.02.2023
• Размер: 199.44 Kb.
• Имя файла: тема 26 Средние величины 2023.docx
• Тип: Литература; #942299
• страница: 1 из 8

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ 4

1. 
   ТЕОРИЯ СТАТИСТИКИ 5
   
   1. 
      Статистические методы наблюдения, классификации
      

и группировки 5

2. 
   Статистические таблицы и графики 18
   
3. 
   Классификация и правила построения статистических
   

показателей 26

4. 
   Средние величины и показатели вариации 36
   
5. 
   Экономические индексы 52
   
6. 
   Выборочное наблюдение 67
   
7. 
   Статистические методы анализа динамики
   

социально-экономических явлений 74

2. 
   СОЦИАЛЬНО-ЭКОНОМИЧЕСКАЯ СТАТИСТИКА 83
   
   1. 
      Статистика продукции 83
      
   2. 
      Статистика труда 92
      
   3. 
      Статистика основных фондов 106
      
   4. 
      Статистика оборотных средств 116
      
   5. 
      Статистика себестоимости продукции 123
      
   6. 
      Статистика финансовых результатов деятельности предприятия 131
      

ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ 139

ЛИТЕРАТУРА 140

ВВЕДЕНИЕ

При переходе к рыночным отношениям большую роль в управлении экономикой играет статистика. С ее помощью осуществляются сбор, науч- ная обработка и анализ статистических данных, характеризующих разви- тие экономики и социально-культурный уровень населения.

Статистика дает возможность изучать взаимосвязи общественных явлений, принимать эффективные управленческие решения на региональных и государствен- ном уровнях, проводить международные сопоставления.

1. Средние величины и показатели вариации

1. Средние величины

Наиболее распространенной формой статистических показателей, ис- пользуемой в социально-экономических исследованиях, является средняявеличина, представляющая собой обобщенную количественную характе- ристику признака в статистической совокупности в конкретных условиях места и времени.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности. В экономи- ческих исследованиях и плановых расчетах применяются две категории средних:

• 
  степенные средние;
  
• 
  структурные средние.
  

К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая,

средняя квадратическая и т. д. Перечисленные средние объединяются об- щей формулой при различных значениях m: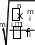

x ,
где x - среднее значение; m - показатель степени средней; x - текущее значение усредняемого признака; n - количество значений признака.

В зависимости от значения показателя степени mразличают следую- щие виды степенных средних:

• 
  при
  
• 
  при
  
• 
  при
  

m 1 - средняя гармоническая m  0 - средняя геометрическая m 1 - средняя арифметическая

^xгар ^; x_г ; ^xар ^;

• 
  при
  

m 2

• 
  средняя квадратическая
  

^xкв ^;

• 
  при
  

m 3

• 
  средняя кубическая
  

^xкуб ^.

При использовании одних и тех же исходных данных чем больше сте- пень, тем больше значение средней величины:

^xгар ^{ x}г ^{ x}ар ^{ x}кв ^{ x}куб ^.

Средняяарифметическаяприменяется в форме простой средней и взвешенной средней.

Средняя арифметическая простая равна простой сумме отдельных значений признака, деленной на общее число этих значений (она применя- ется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):

xx… x



^{ x}i

_{xар } 1 2

n_i1 _.

n n

При расчете средних величин отдельные значения признака, кото- рый осредняется, могут повторяться, поэтому расчет средней величины

n

производится по сгруппированным данным. В этом случае речь идет об использовании среднейарифметическойвзвешенной, которая имеет вид:

_ X_i f_i




n
_Xi1 _.

^{ f}i

i1

Пример 6

Требуется найти среднюю выработку одного рабочего, если известно, сколько деталей изготовил за смену каждый из 15 рабочих, шт.: 21; 20; 20;

19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.

Тогда средняя арифметическая простая

^xар

_ 21  20  20  19  21  19  18  22  19  20  21  20  18  19  20 _

15

 ²⁹⁷  19,8  20 шт.

15

Средняя из вариантов, которые повторяются различное число раз, т. е. имеют различный вес, называется взвешенной. В качестве весов высту- пают численности единиц в разных группах совокупности или их удельный вес. Средняя арифметическая взвешенная вычисляется по формуле:

xfxf… xf



^{ x}i^fi

x_ар 

1 1 2 2

n n_i1 _,

f₁  f₂ …  f_n



^{ f}i

i1

где ка).

f₁, f₂ , …, f_n

• 
  веса (частоты повторения одинаковых значений призна-
  

Пример 7

По данным табл. 17 рассчитать среднюю по трем предприятиям АО заработную плату.

Определим исходное соотношение средней для показателя «Средняя заработная плата»:

_{ЗП } Совокупный фонд заработно йплаты _.

Общая численность ППП

В данном случае средняя заработная плата может быть рассчитана по формуле средней арифметической взвешенной:

^xар

_ 9046  540  9210  275  9130  458 _{ 9111,65 руб.}

540  275  458

Таблица17

Предприятие	Численность промышленно- производственного персонала (ППП), чел.	Средняя заработная плата, руб.
1 2 3	540 275 458	9046 9210 9130

Когда статистическая информация не содержит частот fпо отдельным

вариантам xсовокупности, а представлена как их произведение x f

, при-

меняется формула средней гармонической взвешенной. Обозначим

x f

 w, откуда

f w/ x. Подставляя данное выражение в формулу сред-

ней арифметической взвешенной, получим
ww… w



n




^{ w}i

_{xгар } 1 2

n _i1 _.

n
^w1  ^w2 …  ^wn

_ w_i

x₁ x₂

^{xn i1 x}i

Пример 8

Качество продукции предприятия характеризуется следующими дан- ными за месяц (табл. 18). Определить средний процент брака в целом по предприятию.

Таблица18

Вид продукции	Доля брака, %	Стоимость бракованной продукции, руб.
А В С	1,3 0,9 2,4	2135 3560 980

Расчет средней доли брака выражается соотношением

Долябрака =

Стоимость всей бракованной продукции, руб. _.

Стоимость всей произведенной продукции, руб.

Применяя формулу средней гармонической взвешенной, получаем

_{x } 2135  3560  980
100 % 

6675
100 %  1,1 % .

гар

2135 _

3560 _



⁹⁸⁰ 600619,66

0,013 0,009 0,024

Структурные средние - мода и медиана - в отличие от степенных средних, которые в значительной степени являются абстрактной характе- ристикой совокупности, выступают как конкретные величины, совпадаю- щие с вполне определенными вариантами совокупности.

Модой называется значение признака, которое наиболее часто встре- чается в совокупности (в статистическом ряду). В интервальных рядах распределения с равными интервалами мода вычисляется по формуле (мо- дальный интервал определяется по наибольшей частоте)

f_m f_m

_ f
M_o  x<sub>m

 h</sub>o o1 _,

o


o

m_o

^fmo1

_  _ f_m

^fmo1 ^

m
где x

o

• 
  нижняя граница модального интервала; h - длина модального
  

интервала; f_m, f_m , f_m - частоты в модальном, предыдущем и следую-

o o1 o1
щим за модальным интервалах (соответственно).

Медианойназывается значение признака, которое расположено в се- редине упорядоченного (по возрастанию или убыванию) ряда и разделяет

этот ряд на две равные по численности части. Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметиче- скую из двух срединных значений.

В интервальных рядах распределения медианное значение оказывает- ся в каком-то из интервалов признака x. Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех ча- стот ряда. Значение медианы вычисляется по формуле:

^{ f} S

m

e
M x  h

e

₂ ^me1 _,

f

m
где x

e

m_e

• 
  нижняя граница медианного интервала; h - длина медианного
  

интервала; ^{ f}

2

• 
  половина от общего числа наблюдений;
  

^Sme1

• 
  сумма
  

частот, накопленная до начала медианного интервала; дианного интервала.

f - частота ме-


m
e

Пример 9

Распределение строительных организаций области по стоимости ос- новных фондов (ОФ) представлено в табл. 19.
Таблица19

Группы предприятий по сто- имости ОФ, млн руб.	Число предприятий  f	Накопленная частота Sm
14–16 16–18 18–20 20–22 22–24	2 6 10 4 3	2 8 18 – –

Модальным является третий интервал, так как ему соответствует наибольшая частота, равная 10.

Рассчитываем моду:

M_o  18  2

10  6


(10  6)  (10  4)
 18,8
млн руб.

Итак, модальным значением стоимости основных фондов предприя- тий региона является стоимость, равная 18,8 млн руб. Это означает, что структурное большинство организаций имеют стоимость ОФ, в среднем равную 18,8 млн руб.

Медианным также является третий интервал, поскольку соответству- ющая ему накопленная частота, равная 18, впервые превысила половину суммы всех частот 25 : 2  12,5 . Нижняя граница интервала 18 млн руб., его частота 10, частота, накопленная до него, равна 8. Рассчитываем медиану:

M 18  2^{12,5  8}  18,9 млн руб.

^e ₁₀

Полученный результат говорит о том, что из 25 строительных органи- заций 50 % имеют стоимость основных фондов менее 18,9 млн руб., а 50 % предприятий - более.