Строение и кинематика рычажного механизма(шрм)
 Скачать 234.26 Kb. Скачать 234.26 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Казанский государственный архитектурно-строительный университет Кафедра дорожно-строительные машины Расчетно-графическая работа По дисциплине «Теория механизмов и машин» На тему «Строение и кинематика рычажного механизма(ШРМ)» Вариант 7 Выполнил Студент группы 0ДМ01 Петров Г.Д. Проверил доц.каф. Земдиханов М.М. Казань 2022 1 СТРОЕНИЕ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ. СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА 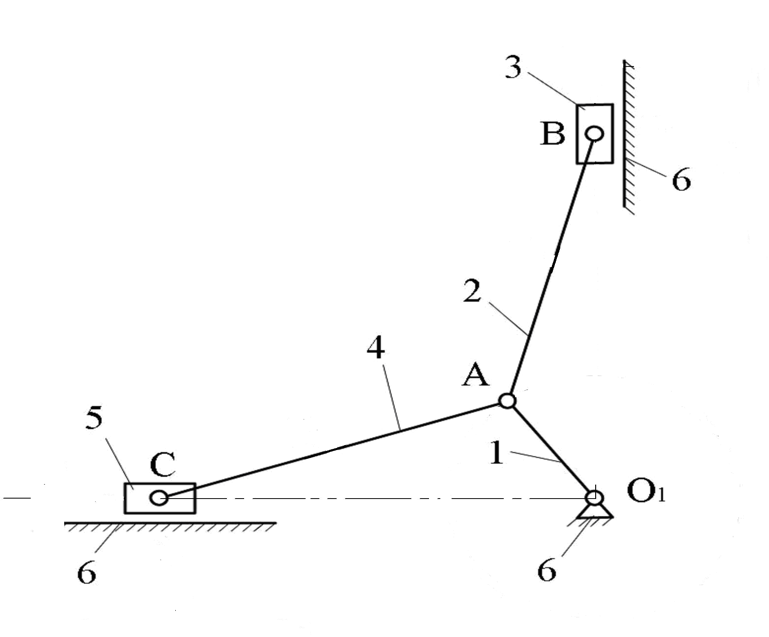 Рисунок 1 – Кинематическая схема механизма 1.1 Определение видов движения звеньев механизма Таблица 1 - Подвижные звенья механизма
1.2 Определение количества и видов относительного движения звеньев в паре и класс пары Таблица 2 - Кинематические пары механизма
1.3 Определение числа степеней свободы механизма Запишем формулу Чебышева. W=3n – 2р5 где, W – число степеней свободы; n – число подвижных звеньев; р5 – число пар 5-го класса. Подставив получим W=3·5 – 2·7 =1 Число степеней свободы рычажного механизма равно 1. 1.4 Разбивка механизма на группы Асура и определение их характеристик Разобьём механизм на группы Асура и рассмотрим каждую группу в отдельности. Выделим первую группу Ассура (звенья 2 и 3). В данном механизме 2 группы Ассура, присоединенные к ведущему кривошипу (начальному механизму), поэтому за первую группу Ассура можем принять любую из них. 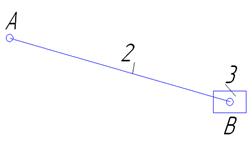 В; B' Рисунок 2 - Первая группа Ассура (звенья 2 и 3) Число подвижных звеньев n =2 (звено 2 и 3). Число кинематических пар 5-го класса р5 =3: A (1-2) – внешняя кинематическая пара B(2-3) – внутренняя кинематическая пара B' (3-0) – внешняя кинематическая пара Тогда W=3·2 – 2·3=0 Следовательно это группа Ассура II класса, 2 порядка и 2 вида Выделим вторую группу Ассура (звенья 4 и 5). 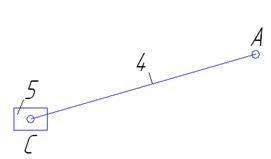 C; C' Рисунок 2 - Вторая группа Ассура (звенья 4 и 5) Число подвижных звеньев n =2 (звено 2 и 3). Число кинематических пар 5-го класса р5 =3: А' (1-4) – внешняя кинематическая пара C (4-5) – внутренняя кинематическая пара С´ (5-0) – внешняя кинематическая пара Тогда W=3·2 – 2·3=0 Следовательно это группа Ассура II класса, 2 порядка и 2 вида Механизма I класса (стойка О, звено ОА и одна пара 5-го класса - О-1). 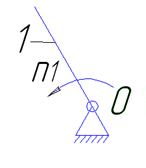 Рисунок 4 - Группа I класса (начальный механизм) Тогда W = 3×1 – 2×1= 1. Следовательно это группа I класса. Механизм образован присоединением к механизму I класса двух групп Ассура II класса 2-го порядка 2 вида. Составим структурную формулу: 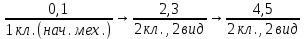 Механизм является механизмом 2 класса, 2 вида. 2 Кинематический анализ рычажного механизма Задание № Таблица 1 - Исходные данные
- угловая скорость кривошипа – 𝜔1 = 40 рад/с; - положения механизма– 11; - масштаб длины – KL = 0,005 м/мм. - отрезок, изображающий на плане скоростей скорость точки А oa = 70 мм. 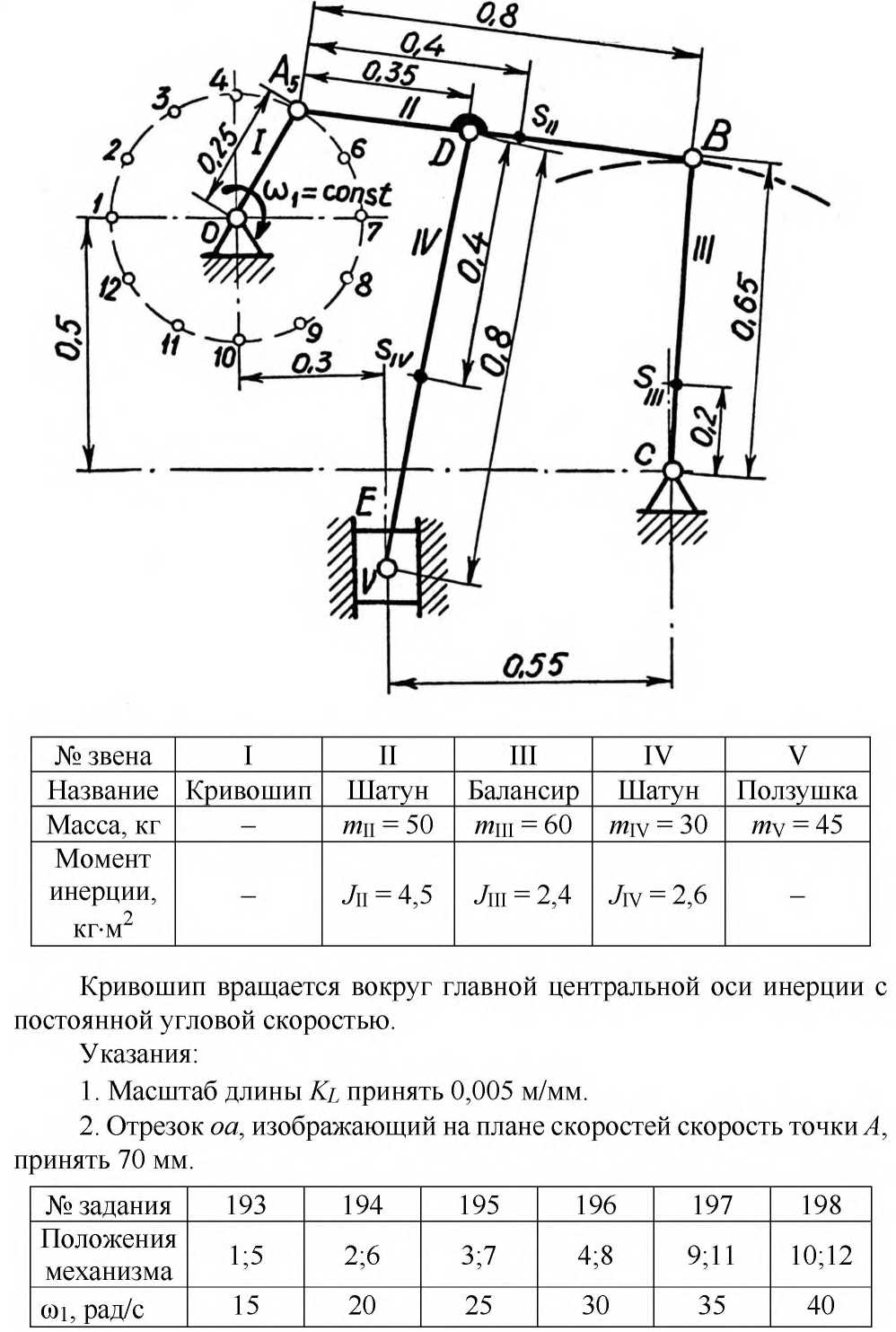 Рисунок 1 - Схема механизма 2.1 Построение планов скоростей Определим скорость точки А. Так как кривошип 1 вращается с постоянной угловой скоростью 𝜔1 (рад/с), то 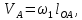 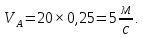 Определим масштаб построения планов скоростей 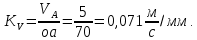 Определим скорость точки В. Составим векторное уравнение скорости точки В 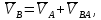 где 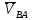 – вектор скорости точки В относительно точки А. – вектор скорости точки В относительно точки А.Направления векторов 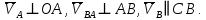 Решим графически данное векторное уравнение. Из плана скоростей 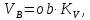 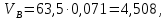 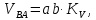 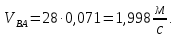 Результаты расчетов занесем в таблицу 2. Определим значение угловой скорости звена 2 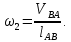 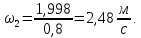 Определим скорость точки D. Из правила подобия определим положение точки D на плане скоростей. Составим пропорцию 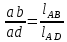 откуда 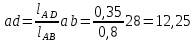 мм ммИз плана скоростей 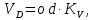 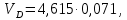 Результаты расчетов занесем в таблицу 2. Определим скорость точки D. Составим систему уравнений для определения положения точки D на плане скоростей 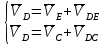 где 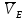 – вектор скорости точки E ( – вектор скорости точки E (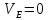 ); );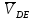 – вектор скорости точки D относительно точки Е; – вектор скорости точки D относительно точки Е;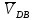 – вектор скорости точки D относительно точки C. – вектор скорости точки D относительно точки C.Направления векторов 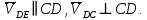 Далее решим графически данную систему векторных уравнений. Из плана скоростей 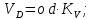 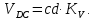 Определим значение угловой скорости 4 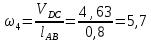 рад/с рад/сРезультаты расчетов занесем в таблицу 2. Определим скорости центров масс звеньев. Положения точек центров масс звеньев 2 и 4 определим из правила подобия. Точка s2 и s4 лежат на отрезках ab и cd соответственно. Составим пропорции для определения расстояния, определяющих их положения на данных отрезках 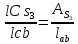 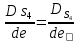 Откуда 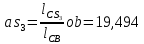 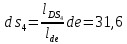 Значение отрезка CD возьмем из плана положений, отрезков ab и cd – из планов скоростей. Из плана скоростей 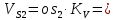 4,66 м/с 4,66 м/с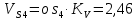 м/с м/сРезультаты измерений и расчетов занесем в таблицу 2. 2.2 Построение планов ускорений Строим планы ускорений для положения 11. Определим ускорение точки А. Так как звено 1 вращается с постоянной скоростью, тангенциальная составляющая ускорения точки А равна нулю, а ускорение точки А равна нормальной составляющей 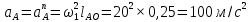 Принимаем длину вектора ускорения точки А на плане ускорений равным 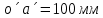 , тогда масштаб построения плана скоростей , тогда масштаб построения плана скоростей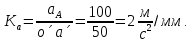 Определим ускорение точки В. Составим векторное уравнение. 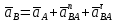 , ,где 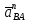 , , 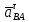 – вектора нормальной и тангенциальной составляющих ускорения точки В относительно точки А. – вектора нормальной и тангенциальной составляющих ускорения точки В относительно точки А.Направления векторов - 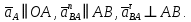 Значение нормальной составляющей 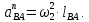 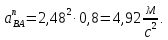 Длина вектора нормальной составляющей на плане ускорений 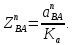 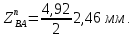 Решим графически систему уравнений для положения 5. Из плана ускорений 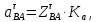 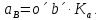 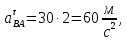 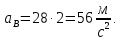 Результаты вычислений занесем в таблицу 3. Определим угловое ускорение звена 2 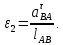 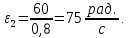 Результаты измерений и вычислений занесем в таблицу. Определим ускорение точки С. Из правила подобия определим положение точки С на плане ускорений. Составим пропорцию 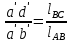 , ,откуда 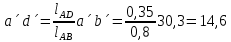 мм ммИз плана ускорений 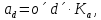 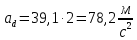 Определим ускорение точки E. Составим векторное уравнение. 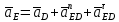 , ,где 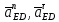 – вектора нормальной и тангенциальной составляющих ускорения точки В относительно точки А. – вектора нормальной и тангенциальной составляющих ускорения точки В относительно точки А.Направления векторов - 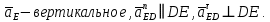 Значение нормальной составляющей 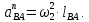 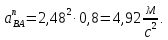 Длина вектора нормальной составляющей на плане ускорений 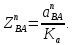 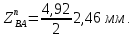 Решим графически систему уравнений для положения 5. Из плана ускорений 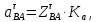 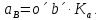 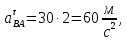 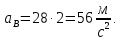 Результаты вычислений занесем в таблицу 3. 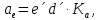 Результаты расчетов занесем в таблицу 3. Определим ускорение точки D. Составим систему уравнений 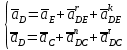 где 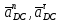 - нормальная и тангенциальная составляющие ускорения точки D относительно точки C; - нормальная и тангенциальная составляющие ускорения точки D относительно точки C;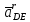 - ускорение точки D относительно точки E; - ускорение точки D относительно точки E;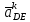 - кориолисово ускорение. - кориолисово ускорение.Направления векторов - 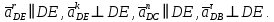 Определим значения нормальной составляющей 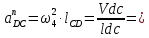 м/с м/сДлины векторов составляющих на плане ускорений 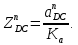 Из плана ускорений 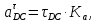 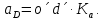 Результаты измерений и расчетов занесем в таблицу 5. Определим угловое ускорение звена 4 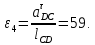 Определим ускорения центров масс звеньев. Положения точек центров масс звеньев 2 и 4 определим из правила подобия. Точка s2 и s4 лежат на отрезках ab и cd соответственно. Составим пропорции для определения расстояния, определяющих их положения на данных отрезках 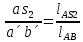 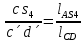 Откуда 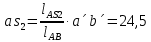 м/с м/с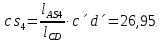 м/с м/сЗначение отрезка CD возьмем из плана положений, отрезков ab и cd – из планов ускорений. Из плана ускорений 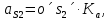 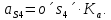 Результаты измерений и расчетов занесем в таблицу 3. Таблица 2 - Результаты расчетов скоростей.
Таблица 3- Результаты расчетов ускорений.
|
