Математический анализ. Типовик 2 (4). типовик 3. Строительство
 Скачать 192.18 Kb. Скачать 192.18 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования «Петербургский государственный университет путей сообщения Императора Александра I» Кафедра «Высшая математика» Типовой расчет №3 «Математический анализ» Вариант № 5 Специальность 08.03.01 «Строительство» Выполнил студент: Киселёв К.В. Группа: АДБ-211 Дата сдачи работы: ______________ Проверил:______________________
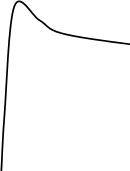
2022 Задание №1. Записать число 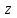 в алгебраической, тригонометрической и показательной формах, изобразив его на комплексной плоскости. в алгебраической, тригонометрической и показательной формах, изобразив его на комплексной плоскости.Вычислить 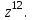 Составить квадратное уравнение, одним из корней которого является число 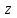 . . 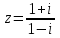 2) 2) 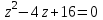 . .Решение: 1) Приведем 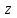 к алгебраической форме комплексного числа. Для этого умножим числитель и знаменатель дроби на число к алгебраической форме комплексного числа. Для этого умножим числитель и знаменатель дроби на число 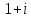 , сопряженное знаменателю. , сопряженное знаменателю.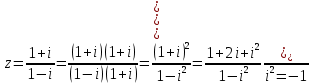 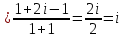 Итак, 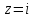 алгебраическая форма комплексного числа алгебраическая форма комплексного числа 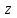 . .Изобразим z на комплексной плоскости: 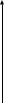   Запишем z в тригонометрическом виде: Имеем: 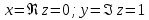 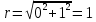 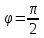 (ну, тут всё очевидно) (ну, тут всё очевидно)Таким образом, тригонометрическая форма комплексного числа z = (1+I)/(1-I) 2. Находим показательную форму комплексного числа z = (1+I)/(1-I) y         Итак, тригонометрическая запись числа z: 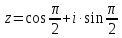 В показательной форме: 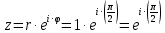 φ 1 0 x Вычислим 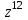 , используя формулу: , используя формулу: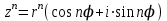 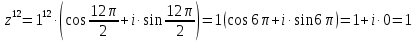 z = i 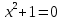 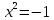 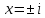 2) 1. 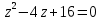 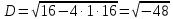 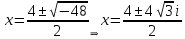 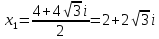 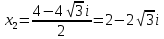 Изобразим z на комплексной плоскости: 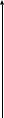                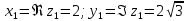 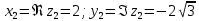 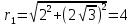 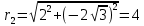 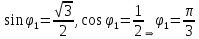 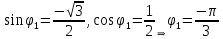 φ1 φ2 0 2 x 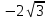 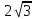 y Запишем числа 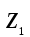 и и 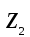 в тригонометрической и показательной форме. в тригонометрической и показательной форме.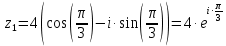 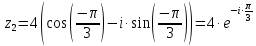 2. 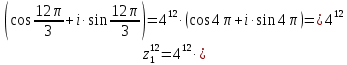 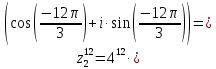 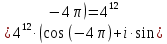 Задание № 2 Вычислить пределы. 1. 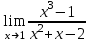 2. 2. 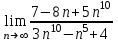 3. 3. 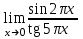  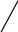 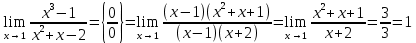 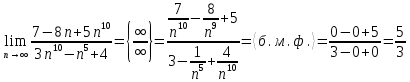 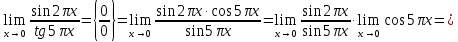 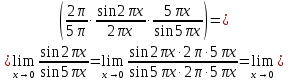 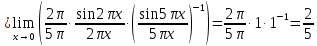 I замеч. пред. Задание №3 Подобрать параметры 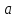 и и 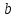 так, чтобы функция так, чтобы функция 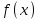 была непрерывна. была непрерывна.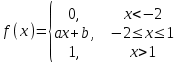 Функция 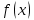 составлена из элементарных функций, каждая из которых непрерывна на указанных промежутках. Непрерывность может нарушаться только в точках составлена из элементарных функций, каждая из которых непрерывна на указанных промежутках. Непрерывность может нарушаться только в точках 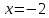 и и 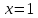 . . Вычислим односторонние пределы функции 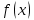 в этих точках. в этих точках.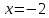 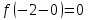 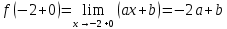 Условие непрерывности функции в точке: 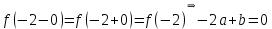 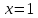 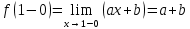 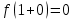 Условие непрерывности функции в точке: 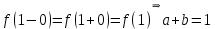 Получаем систему уравнений: 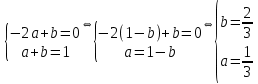 Решение системы дает значения искомых параметров: 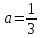 , , 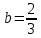 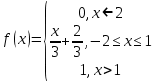 Задание №4 Продифференцировать данные функции по переменной 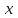 . .1) 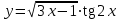 ; 2) ; 2) 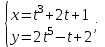 3) 3) 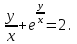 1) 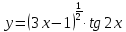 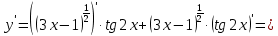 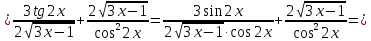 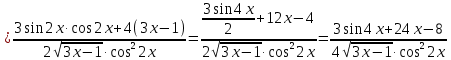 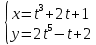 Производная 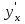 находится по формуле: находится по формуле: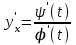 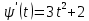 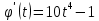 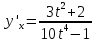 3) 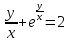 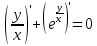 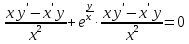 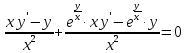 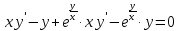 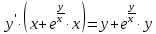 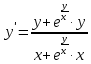 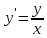 Задание №5 Исследовать функцию с помощью производной и построить её график. 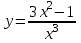 ООФ: 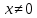 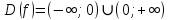 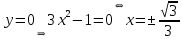 Следовательно график функции пересекает ось Oxв точках 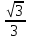 и и 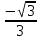 . .При 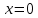 значение функции не определено, следовательно график функции не имеет точек пересечения с осью Oy. значение функции не определено, следовательно график функции не имеет точек пересечения с осью Oy.Исследование функции на четность (нечетность). 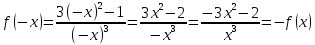 Следовательно функция нечетная. Функция непериодическая. Исследование непрерывности. Классификация точек разрыва. Функция терпит разрыв в точке 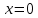 . Определим тип разрыва: . Определим тип разрыва: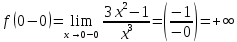 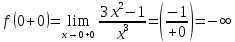 Односторонние пределы функции бесконечны, следовательно, 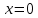 – точка разрыва второго рода (точка бесконечного разрыва). – точка разрыва второго рода (точка бесконечного разрыва).Интервалы монотонности, точки экстремума функции. 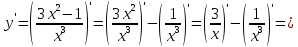 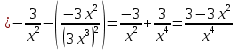 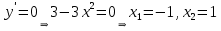          + + - -            x 0 1 -1     Точки экстремума: Функция имеет минимум при 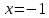 , так как при переходе через эту точку производная меняет знак с (-) на (+), причем , так как при переходе через эту точку производная меняет знак с (-) на (+), причем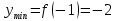 Функция имеет максимум при 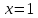 , так как при переходе через эту точку производная меняет знак с (+) на (-), причем , так как при переходе через эту точку производная меняет знак с (+) на (-), причем 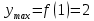 Функция возрастает при 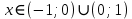 Функция убывает при 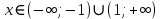 Интервалы выпуклости и точки перегиба. 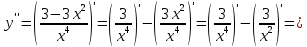 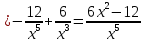 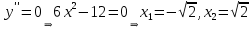 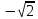 и и 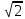 – точки перегиба функции – точки перегиба функции     + + - - 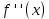             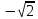 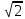 x 0 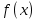  Функция выпукла при 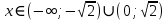 Функция вогнута при 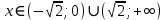 Асимптоты Прямая 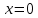 является вертикальной асимптотой графика функции является вертикальной асимптотой графика функции(см. пункт 5). Найдем наклонные асимптоты 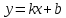 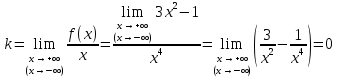 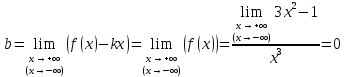 Итак, график имеет наклонную асимптоту 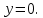 График функции  y       x
|