9 класс. СУММАТИВНОЕ ОЦЕНИВАНИЕ 9 класс алгебра и геометрия. Суммативное оценивание за раздел уравнения, неравенства с двумя переменными и их системы

Оценивание заданий работы

№ задания

Количество баллов

Всего баллов

20 баллов

Название	Суммативное оценивание за раздел уравнения, неравенства с двумя переменными и их системы
Анкор	9 класс
Дата	07.12.2022
Размер	2.92 Mb.
Формат файла
Имя файла	СУММАТИВНОЕ ОЦЕНИВАНИЕ 9 класс алгебра и геометрия.docx
Тип	Документы #832398
страница	22 из 24

1 ... 16 17 18 19 20 21 22 23 24

2 ВАРИАНТ

1. Радиус окружности, вписанной в треугольник, равен 14, а периметр треугольника 58. Найдите площадь треугольника.

[2]
2. Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны:

а) 5; 7 и 9; b) 5; 6 и 7; с) 6; 8 и 10.

[3]

3. В треугольнике АВС известно, что АВ = 14 см, ВС = 10 см, sin A = 0,3. Найдите синус угла Стреугольника.

[2]

4. Основания равнобокой трапеции ABCD равны 10 см и 22 см, а высота – 8 см. Найдите:

диагональ трапеции АС;
радиус окружности, описанной около трапеции.

[6]

5. Определите ширину реки ABдля геодезических измерений как показано на рисунке:

В 105⁰ ,

С 30⁰ ,

ВС  240 м.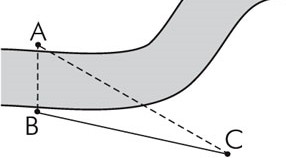

[3]

^6.^{К одной точке приложили две силы:}^F1 ^{= 12 H и}^F2 ^{= 20 H под углом 60°. Найдите} равнодействующую этих двух сил. Выполните рисунок.

[4]

Схема выставления баллов

2 вариант

3 ВАРИАНТ

1. Радиус окружности, вписанной в треугольник, равен 16, а периметр треугольника равен 60. Найдите площадь треугольника.

[2]
2. Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны:

а) 5; 8 и 10; b) 6; 7 и 8; с) 3; 4 и 5.

[3]

3. В треугольнике АВС известно, что АВ = 14 см, ВС = 10 см, sin A= 0,4. Найдите синус угла Стреугольника.

[2]

4. Основания равнобокой трапеции ABCDравны 11 см и 23 см, а высота – 8 см. Найдите:

диагональ трапеции АС;
радиус окружности, описанной около трапеции.

[6]
5. Определите ширину реки ABдля геодезических измерений как показано на рисунке:

В 105⁰ ,

С 30⁰ ,

ВС  260 м.

[3]

^6.^{К одной точке приложили две силы:}^F1 ^{= 14}^H^и^F2 ^{= 20}^H^{под углом 60°. Найдите} равнодействующую этих двух сил. Выполните рисунок.

[4]

Схема выставления баллов

3 вариант

4 ВАРИАНТ

1. Радиус окружности, вписанной в треугольник, равен 18, а периметр треугольника равен 62. Найдите площадь треугольника.

[2]
2. Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны:

а) 3; 6 и 7; b) 7; 8 и 10; с) 6; 8 и 10.

[3]

3. В треугольнике АВС известно, что АВ = 12 см, ВС = 10 см, sin A= 0,4. Найдите синус угла Стреугольника.

[2]

4. Основания равнобокой трапеции ABCDравны 12 см и 24 см, а высота – 8 см. Найдите:

диагональ трапеции АС;
радиус окружности, описанной около трапеции.

[6]
5. Определите ширину реки ABдля геодезических измерений как показано на рисунке:

В 105⁰ ,

С 30⁰ ,

ВС  270 м.

[3]

^6.^{К одной точке приложили две силы:}^F1 ^{= 15}^H^и^F2 ^{= 20}^H^{под углом 60°. Найдите} равнодействующую этих двух сил. Выполните рисунок.

[4]

Схема выставления баллов

4 вариант

.
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ

Обзор суммативного оценивания

Продолжительность – 40 минут

Количество баллов – 20

Типы заданий:

МВО – задания с множественным выбором ответов;

КО – задания, требующие краткого ответа;

РО – задания, требующие развернутого ответа.

Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с множественным

выбором ответов, с кратким и развернутым ответами.

В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.

В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде

численного значения, слова или короткого предложения.

В вопросах, требующих развернутого ответа, обучающийся должен показать всю

последовательность действий в решении заданий для получения максимального балла.

Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов

Характеристика заданий суммативного оценивания

Раздел	Проверяемая цель	Уровень мыслительных навыков	Кол. заданий*	№ задания*	Тип задания*	Время на выполнение, мин*	Балл*	Балл за раздел
Окружность. Многоугольники	9.1.2.2 Знать определение и свойства правильных многоугольников	Знание и понимание	1	1	МВО	2	1	20
	9.1.1.1 Выводить и применять формулу длины дуги	Применение	1	2	МВО	2	1
	9.1.2.1 Знать и применять свойства и признаки вписанных и описанных четырёхугольников	Применение	1	3	КО	6	4
	9.1.2.5 Знать и применять формулы, связывающие стороны, периметр, площадь правильного многоугольника и радиусы вписанной и описанной окружностей правильного многоугольника	Применение	1	4	РО	8	4
	9.1.2.6 Знать и применять свойства медиан треугольника	Применение	1	5	РО	10	5
	9.1.1.2 Выводить и применять формулу площади сектора, сегмента	Применение	1	6	РО	12	5
ИТОГО:						40	20	20

ЗАДАНИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ

1 ВАРИАНТ

1. Найдите количество сторон правильного многоугольника, если сумма всех его внутренних углов равна 1440°.

А) 8 В) 9 С) 10 D) 12

2. Дана окружность радиуса 10 см . Чему равна длина ее дуги с градусной мерой 90°?

А) 4 см В) 6 см С) 8 см D) 5 см
3. Три угла четырехугольника, вписанного в окружность, взятые в порядке следования, относятся как 4 : 3 : 5. Найдите углы четырехугольника.

4. В окружность вписан квадрат со стороной 3 √2 см. Найдите площадь правильного треугольника, описанного около этой окружности.

5. Основание АВ треугольника АВС равно 26 см. Медианы АК и ВМ, проведенные к боковым сторонам, равны соответственно 30 см и 39 см. Найдите площадь треугольника АВС.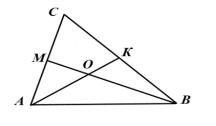

6. На рисунке изображен сектор круга с центром в точке O и радиусом, равным 4 см. ОD = 2 см и DOС  45°. Найдите площадь закрашенной области.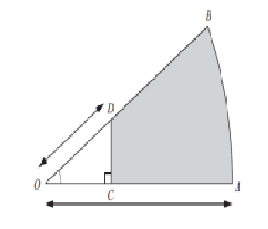

1 ... 16 17 18 19 20 21 22 23 24