Решение задач. Сводка и группировка в статистике
 Скачать 0.63 Mb.
|
|
Задача 2. Имеются следующие данные о стоимости имущества предприятия (млн руб) (табл.1). Определить абсолютное и относительное изменение среднегодовой стоимости имущества предприятия в 2000 г. по сравнению с 1998 и 1999 гг. Таблица 1
Решение Поскольку промежутки времени между датами равны, средний уровень моментного ряда динамики исчисляется по формуле 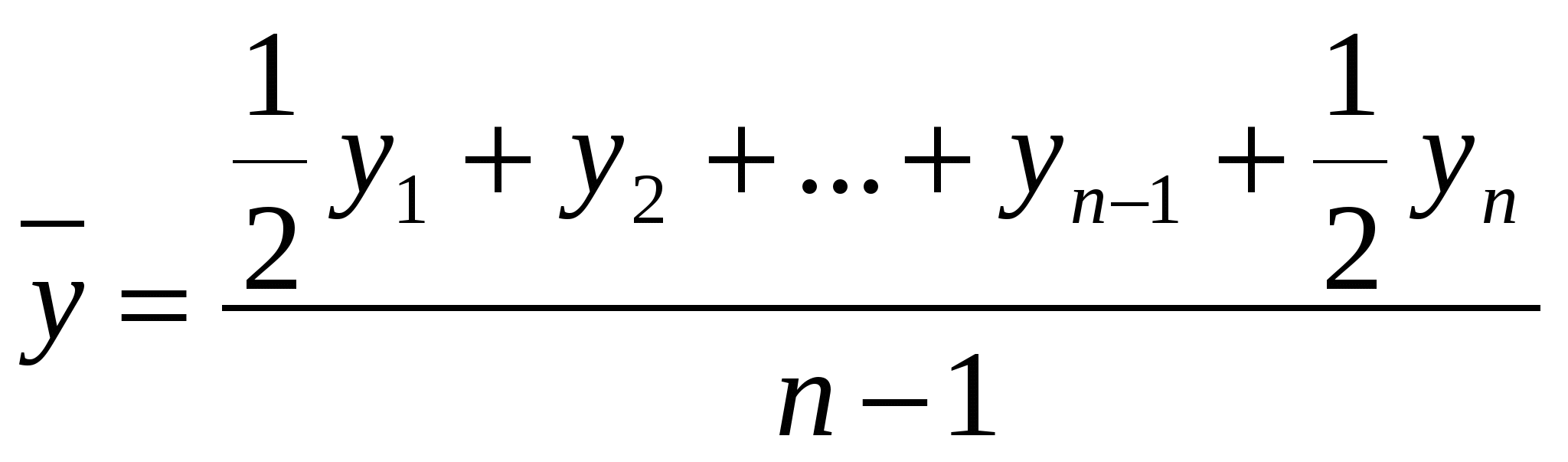 ,где y1 и yn-уровни соответственно на начало и на конец периода за который исчисляется средний уровень; n- число уровней ряда.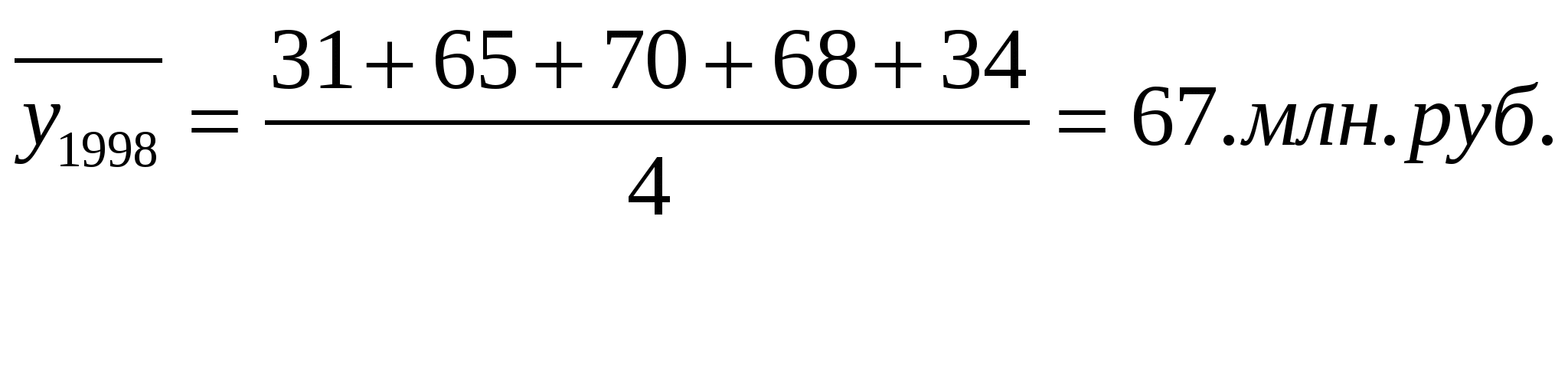 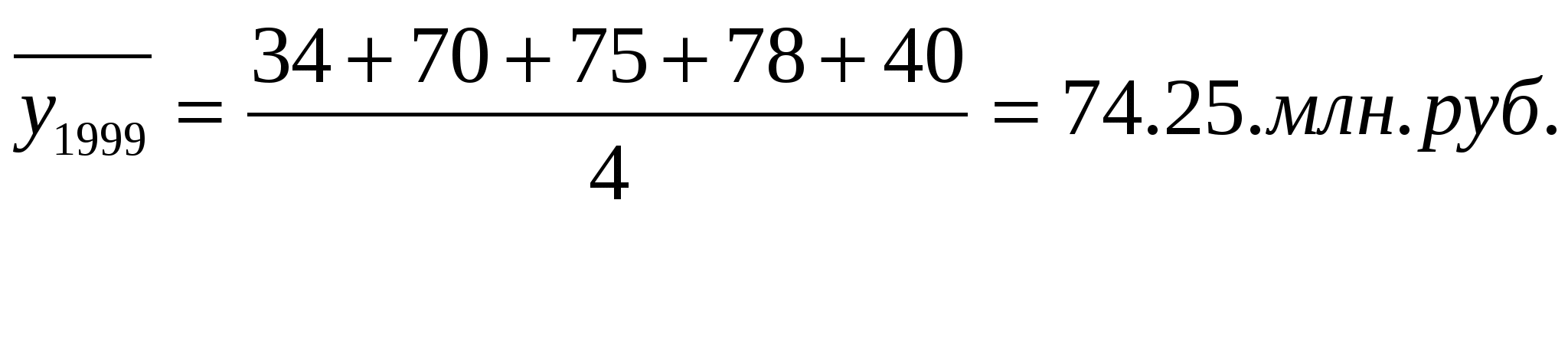  В 2000 г. среднегодовая стоимость имущества предприятия возросла по сравнению с 1998 г. на 20.375 млн., или на 3.04 %, и по сравнению с 1999 – на 13.125 млн. руб., или на 17.7 %. Задача 3.Количество дорожно-транспортных происшествий, совершенных водителями в регионе увеличилось в 1995 г. по сравнению с 1990г. на 2 тыс., или на 4%; в 1997 г. по сравнению с 1995г. их число возросло на 30%, а в 2000 г. по сравнению с 1997 г. их число возросло на 2%. Определите количество ДТП в 1990, 1995. 1997, 2000 гг. Решение Уровень ДТП в 1990 г. определяется по формуле:  ,где  абсолютная величина 1% прироста для 1995 г.;  Далее, недостающие уровни 1995, 1997, 2000 гг. определим, зная темпы роста для соответствующего периода, тыс. ед.:    Индексы и их использование в экономико-статистическом анализе Задача 1. Имеются следующие данные о реализации плодово-ягодной продукции в регионе (табл. 1).Определите: а) сводный индекс товарооборота; б) сводный индекс цен; в) индекс физического объема реализации; г) взаимосвязь исчисленных индексов. Таблица 1
Решение а) Для сравнения товарооборота в текущем периоде с его величиной в базисном периоде используется сводный индекс товарооборота:  = =0,969 или 96,9%Таким образом, товарооборот в целом по данной товарной группе в текущем периоде по сравнению с базисным уменьшился на 3,1% (100-96,9). Отметим, что объем товарной группы при расчете этого и последующего индексов значения не имеет. б) Вычислим сводный индекс цен:  = =0,892 или 89,2 %То есть по данной товарной группе цены в августе по сравнению с июлем снизились на 10,8% (100-89,2). Числитель и знаменатель сводного индекса цен можно интерпретировать с точки зрения потребителей. Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные товары в текущем периоде. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак «-») или перерасхода («+») покупателей от изменения цен:  - =618-693=- 75 тыс. руб.в) Индекс физического объема реализации составит:  = =1,086 или 108,6 %.Физический объем реализации (товарооборота увеличился на 8,6%. г) Используя взаимосвязь индексов, проверим правильность вычислений: =x=0,892 x01,086=0,969 или 96,9 %.Задача 2. Имеются следующие данные о производстве и себестоимости молока в ряде районов Орловской области (табл. 1). Определите: а) индекс затрат; б) индекс себестоимости фиксированного состава; в) индекс объема и структуры затрат; г) взаимосвязь индексов. Таблица 1 Производство и себестоимость 1 ц молока
Решение а) Индекс затрат характеризует изменение затрат на производство молока в хозяйствах области в 2000 г. по сравнению с 1999 г.: Iзатрат=  =83511,4/56323,2=1,48 или 148%б) Индекс себестоимости фиксированного состава характеризует изменение затрат за счет изменения себестоимости единицы продукции в отдельных районах: Iс/с фикс. состава.=  =83511,4/42794,6 =1,9 или 190%в) Индекс объема и структуры затрат характеризует изменение затрат на производство молока за счет изменения количества и структуры произведенной продукции: Iобъема и структуры.=  = 42794,6/56323,2=0,76 или 76%г) Взаимосвязь индексов: Iзатрат= Iс/с фикс. состава х Iобъема и структуры 1,48=1,9 х0,76 Таким образом, в 2000 г. по сравнению с 1999 г. затраты на производство молока в анализируемых районах Орловской области увеличились на 48%. Увеличение затрат произошло за счет роста себестоимости 1 ц молока в отдельных районах в среднем на 90%. Однако уменьшение объема производства молока и изменения его структуры привело к уменьшению затрат на 24%. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||