Решение задач. Сводка и группировка в статистике
 Скачать 0.63 Mb.
|
|
Задача 2. По приведенным ниже данным о квалификации рабочих цеха требуется: а) построить дискретный ряд распределения; б) дать графическое изображение ряда. Тарифные разряды 24 рабочих цеха: 3;6;4;4;2;3;5;4;4;5;2;3;4;4;5;2;3;6;5;4;2;4;3. Решение а) Дискретный ряд распределения имеет вид (табл.1). Таблица 1 Распределение рабочих цеха по квалификации
б)на рис. 3.1. представлено графическое изображение построенного дискретного вариационного ряда в виде полигона частот. Полигон частот замыкается, для этого крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе (в данном случае х=1 и х=7). 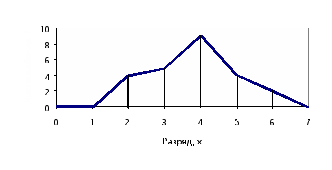 Рис. 3.1. Полигон распределения рабочих цеха по квалификации Задача 3.Имеются следующие данные о возрастном составе рабочих цеха (лет): 18;38;28;29;26;38;34;22;28;30;22;23;35;33;27;24;30;32;28;25;29;26;31;24;29;27;32;25;29;29. Для анализа распределения рабочих цеха по возрасту требуется: а) построить интервальный ряд распределения; б) графически изобразить ряд. Решение а) Величина интервала группировки определяется по формуле:  =2,85≈3 года, где n принимаем равным 7.Интервальный ряд представлен в таблице 1. Таблица 1 Интервальный ряд распределения
б) Графически интервальный вариационный ряд может быть представлен в виде гистограммы, полигона, кумуляты. На рис.1 представлен интервальный полигон частот. На рис.2 представлена кумулятивная кривая (кумулята).  Рис. 1 Полигон распределения рабочих цеха по возрасту 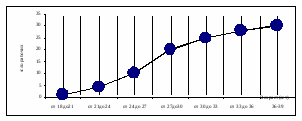 Рис.2 Кумулята распределения рабочих цеха по возрасту Средние величины в статистике Задача 1. Имеются следующие данные о заработной плате рабочих участка (табл.1) Таблица 1
Вычислить среднюю месячную заработную плату рабочих участка. Решение Процесс выбора средней таков: а) определяющий показатель - общая сумма начисленной заработной платы; б) математическое выражение определяющего показателя-  в) замена индивидуальных значений средними -  г) решение уравнения:  Следовательно, использовалась формула простой средней арифметической. Задача 2. Распределение рабочих участка по стажу работы следующее (табл.1) Определить средний стаж работы рабочих участка. Таблица 1
Решение Определяющий показатель – общий стаж работы всех рабочих-  .Средний стаж работы-  лет.Для каждого интервала предварительно вычислялось среднее значение признака как полусумма нижнего и верхнего значения интервала. Величина открытых интервалов приравнивается к величине примыкающих к ним соседних интервалов:     Для решения задачи использовалась формула средней арифметической взвешенной. Задача 3. За два месяца по цехам завода имеются следующие данные (табл.1.) Определить за какой месяц и на сколько процентов была выше средняя месячная заработная плата работников предприятия. Решение Введем условные обозначения для сентября: f -численность работников по каждому цеху; x-средняя месячная заработная плата работников каждого цеха; определяющий показатель- общий фонд заработной платы-  Таблица 1
Средняя месячная заработная плата работников предприятия за сентябрь составила:  руб.Условные обозначения для октября следующие: w -фонд заработной платы по каждому цеху;  -средняя месячная заработная плата работников каждого цеха;определяющий показатель –  Средняя месячная заработная плата работников предприятия за октябрь равна: 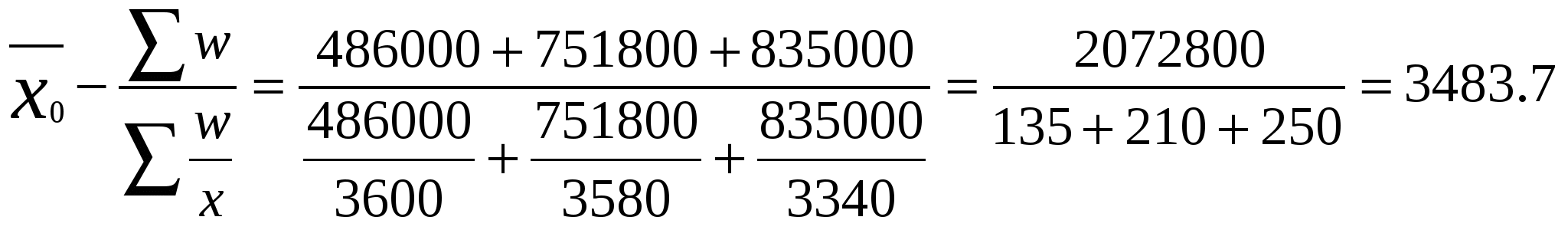 где  - численность работников каждого цеха в октябре.Средняя месячная заработная плата в октябре исчислена по формуле взвешенной гармонической. Динамика средней месячной заработной платы работников предприятия: 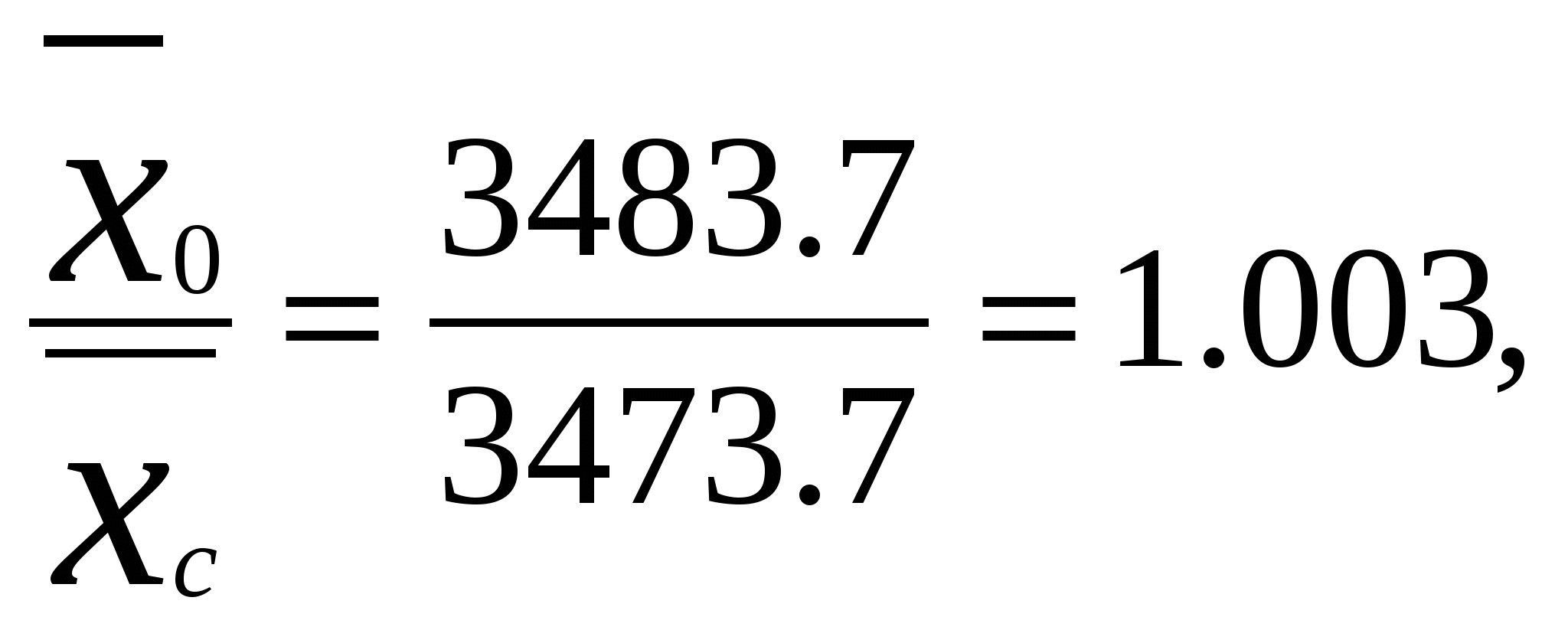 или 100.3%Следовательно, средняя месячная заработная плата работников предприятия в октябре повысилась на 0.3% по сравнению с сентябрем. Задача 4. Проведена малая выборка из партии электрических лампочек для определения продолжительности их службы. Результаты представлены в табл.1. Определить моду и медиану. Таблица 1
Решение Для определения моды и медианы производится ранжирование данных. Ранжированный ряд: 1270, 1370, 1380, 1400, 1400, 1400, 1420, 1430, 1450. Мода-  ч (1400-значение признака, встречающееся три раза).Место медианы-  Ме=1400 ч (1400- значение признака, находящееся на 5-м месте в ранжированном ряду). . Показатели вариации и анализ частотного распределения Задача 1. По приведенным ниже данным о квалификации рабочих требуется вычислить показатели вариации. Тарифные разряды 24 рабочих цеха: 4;3;6;4;4;2;3;5;4;4;5;2;3;4;4;5;2;3;6;5;4;2;4;3. Решение Построим дискретный ряд распределения (табл.1). Вычислим среднюю арифметическую взвешенную:  разряда.Таблица 1 Распределение рабочих цеха по квалификации
К показателям вариации относятся: среднее линейное отклонение ( 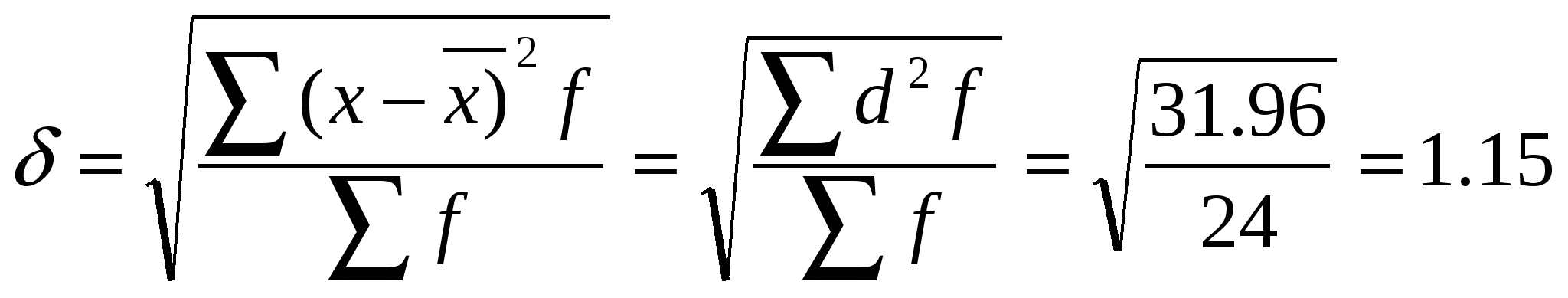 ), среднее квадратическое отклонение ( ), коэффициент вариации (v). Для расчета показателей ряда распределения удобно использовать вспомогательную таблицу 2.= разряда;  разряда; Таблица 2 Расчет показателей вариации
Следовательно, индивидуальные значения отличаются в среднем от средней арифметической на 1.15 разряда, или на 30.3%. Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойствами мажорантности средних. Значение коэффициента вариации (30.3 %) свидетельствует о том, что совокупность достаточно однородна. Задача 2. Имеются следующие данные о возрастном составе рабочих цеха (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29. Для анализа распределения рабочих цеха по возрасту: построить интервальный ряд распределения; исчислить показатели вариации. Решение Построим интервальный ряд распределения.(табл. 1) Таблица 1
Для расчета показателей вариации составляется вспомогательная таблица (табл.2) Таблица 2 Вспомогательная таблица для расчета показателей вариации
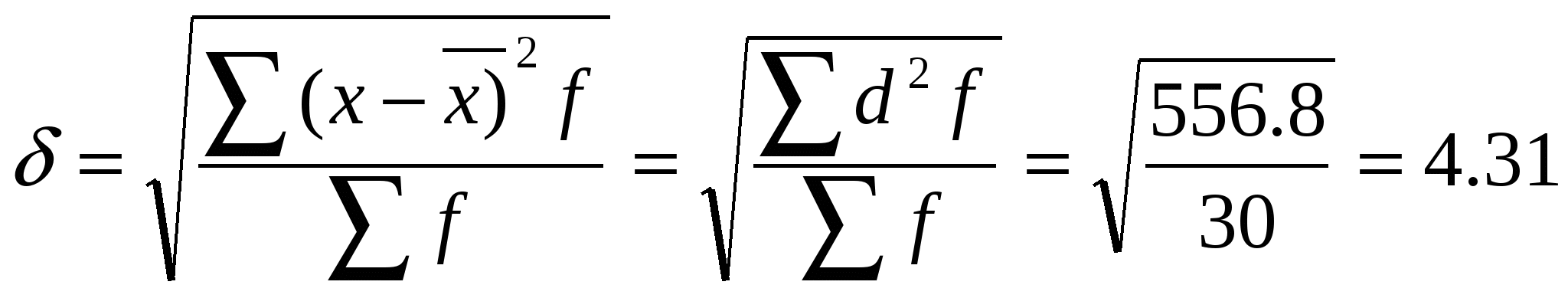= года года Следовательно, вариация возраста у рабочих данного цеха не является значительной, что подтверждает достаточную однородность совокупности. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
