Название свойств
|
Определение
|
Графики функции
|
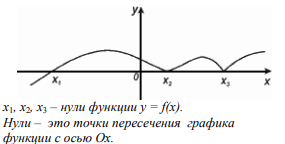
Нули функции
|
Нулём функции называется то значение х, при котором функция обращается в 0, то есть f (x) 0.
|
|
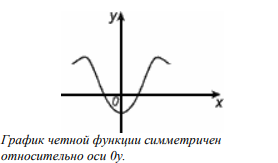
Четность функции
|
Функция называется чётной, если для любого х из области определения выполняется равенство f (x) f (x)
|
|
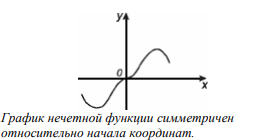
Нечетность функции
|
Функция называется нечётной, если для любого х из области определения выполняется равенство f (x) f (x)
|
|
|
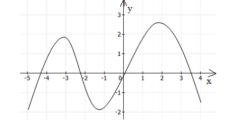
Функция, которая не является ни чётной, ни нечётной называется функцией общего вида
|
|
Возрастание функции
|
Функция f (x) называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е.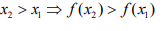
|
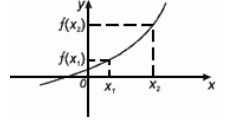
|
Убывание функции
|
Убывание функции Функция f (x) называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е. 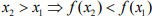
|
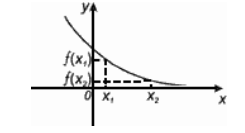
|
|
Промежутки, на которых функция либо только убывает, либо только возрастает называются промежутками монотонности.
|
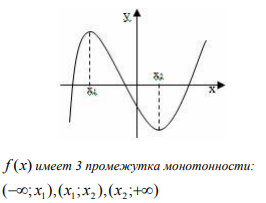
|
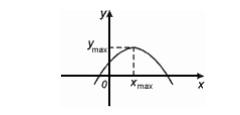
Локальный максимум
|
Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: 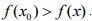
|
|
Локальный минимум
|
Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: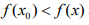
|
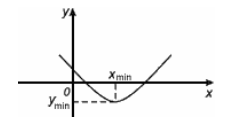
|
|
Точки локального максимума и точки локального минимума называются точками локального экстремума.
|
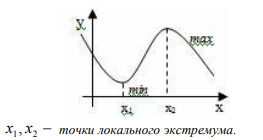
|
Периодичность функции
|
Функция f(x) называется периодичной, с периодом Т, если для любого х выполняется равенство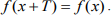
|
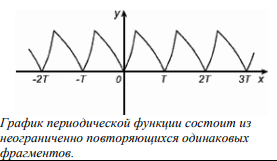
|
Промежутки знакопостоянства
|
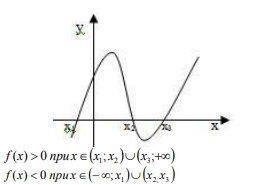
Промежутки, на которых функция либо только положительна, либо только отрицательна, называются промежутками знакопостоянства.
|
|
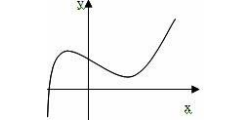
Непрерывность функции
|
Функция f (x) называется непрерывной в точке x0, если предел функции при 0 x x равен значению функции в этой точке, т.е.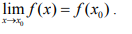
|
|
Точки разрыва
|
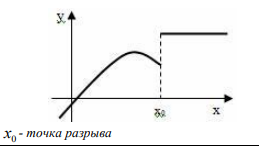
Точки, в которых нарушено условие непрерывности называются точками разрыва функции.
|
|
Обратная функция
|
Обратная функция Функцию y=f(x), x∈X называют обратимой, если любое своё значение она принимает только в одной точке множества X (иными словами, если разным значениям аргумента соответствуют разные значения функции). Если функция y=f(x), x∈X монотонна на множестве X, то она обратима.
|
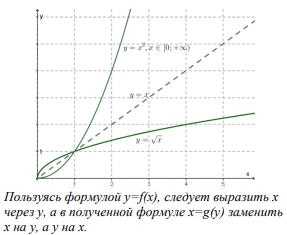
|
 Скачать 178.76 Kb.
Скачать 178.76 Kb.