Лекции по гидравлике (Полная версия). Техническая аэрогидродинамика
 Скачать 6.88 Mb.
|
|
Задача 3. Дано: размеры трубопроводов (кроме диаметра d), шероховатость его стенок  , свойства жидкости , напор Н, расход Q. Определить диаметр трубопровода.Решение. При решении этой задачи возникают затруднения с непосредственным определением значения 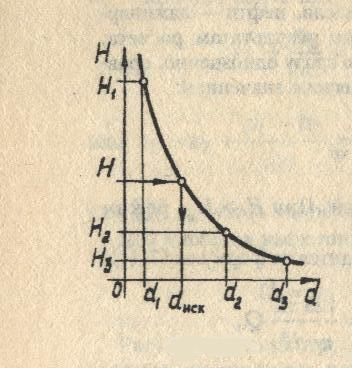 , аналогичные задаче второго типа. Поэтому решение целесообразно выполнять графоаналитическим методом. Задается несколько значений диаметров  .Для каждого  находится соответствующее значение напора Н при заданном расходе Q (п раз разрешается задача первого типа). По результатам расчетов строится график  . По графику определяется искомый диаметр d, соответствующий заданному значению напора Н.  Гидравлический расчет сифонного трубопровода. Сифон — это простой самотечный трубопровод, одна часть которого расположена выше свободной поверхности питающей его жидкости, а другая ниже. 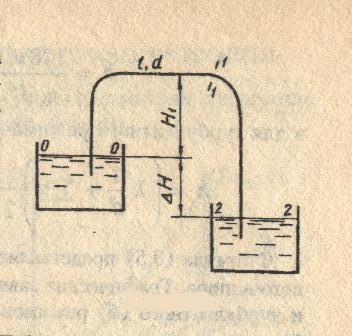 Жидкость движется в сифоне за счет разности уровней Н. Заметим, чтобы началось движение по сифону, необходимо весь его объем заполнить жидкостью. Учтем, что для свободных поверхностей 0-0 и 2-2  и суммарное сопротивление складывается из потерь на трение по длине и местных, и запишем уравнение Бернулли: ИЛИ  где Н представляет потребный (располагаемый) напор  .Формула показывает, что расход жидкости через сифон не зависит от высоты ее подъема  . Однако при увеличении давление жидкости  снижается, вплоть до давления насыщенных паров, при котором в сечении 1-1 возникает кавитация и расход уменьшается, вплоть до полного прекращения движения жидкости. Предельное значение  рассчитывается по уравнению Бернулли для участка 0-1.Преобразуем уравнение к виду  Потребным напором для простого трубопровода называется напор в начальном сечении, обеспечивающий заданный расход Q жидкости в трубопроводе.Введя обозначение  перепишем в виде: где  и  имеют разные значения в зависимости от режима течения. Для ламинарного режима с учетом местных сопротивлений эквивалентными длинами имеем ,а для турбулентного режима -  .Формула представляет собой уравнение кривой потребного напора. Графические зависимости для ламинарного (а) и турбулентного (б) режимов приведены на рис. Величина  , когда жидкость поднимается с меньшей высоты на большую, и  при течении сверху вниз (при условии  ). Крутизна кривых зависит от коэффициента и возрастает с увеличением длины трубопровода, с уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.Иногда вместо кривых потребного напора удобнее пользоваться характеристикой трубопровода, под которой понимают зависимость суммарных потерь напора (или давления) в трубопроводе от расхода 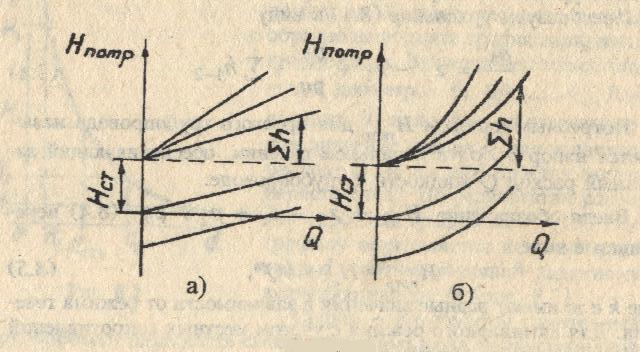 . Таким образом, характеристика трубопровода представляет собой кривую потребного напора, смещенную в начало координат. Элементы теории свободных струй. Воздушные тепловые завесы. Свободная струя- поток жидкости, не ограниченной твердыми стенками. Свободные струи: 1)затопленная- если она распространяется в пространстве, занятом жидкостью( капельной или газообразной), однородной с данной ( например струя воды, выходящая из отверстия резервуара при истечении «под уровень», или струя воздуха, выходящая из отверстия замкнутого резервуара в атмосферу в условиях одной и той же плотности воздуха). 2)незатопленная –( например, струя воды при истечении из резервуара в атмосферу, когда эта струя находится в свободном полете). В прошлом в связи с запросами водопроводной техники( уже в 18 веке при устройстве дворцовых фонтанов в Версале, Петергофе) исследовалась задача о высоте подъема свободной незатопленной струи h и дальности ее полета l в зависимости от угла 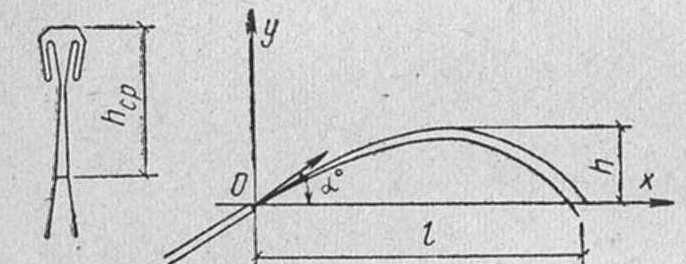 наклона струи к горизонту в начальном ее сечении (рис.1), а в связи с запросами турбостроения- вопрос о динамическом воздействии струи на обтекаемые ею пластинки. рис.1 Развитие современной техники потребовало более глубокого изучения этой области гидродинамики. В настоящее время теория свободных струй и методы их практического приложения составляют обширный раздел гидравлики. Теоретические и экспериментальные исследования показали, что струя, выходящая из отверстия с насадком в условиях плавного очертания входа в насадок и при условии, что давление на выходе из него не превышает «критического» ( в случае истечения газа), постепенно расширяется в виде конуса и благодаря вязкости увлекает в движение окружающую ее жидкость. Вместе с тем между струей и жидкостью внешнего пространства происходит обмен масс, причем в процессе этого обмена струя захватывает все большую массу, так что в направлении движения струи ее масса несколько увеличивается. Структура струи По исследованиям Г.Н.Абрамовича движение жидкости, образующей струю, можно характеризовать следующим 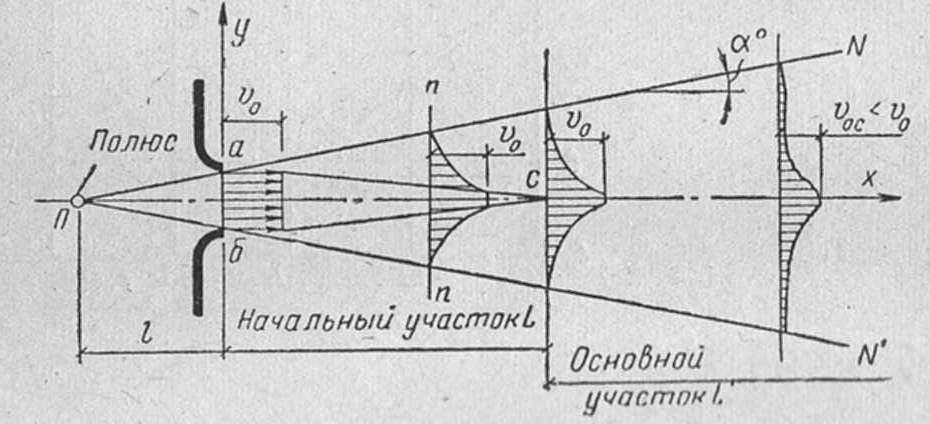 образом.(рис.2) В выходном сечении а-б скорости потоков потока во всех точках сечения равны между собой. На протяжении длины L ( на так называемом начальном участке) осевая скорость постоянна по величине и равна скорости выходного сечения V  .В некотором промежуточном сечении n начального участка эпюра скоростей имеет вид ,указанный на рис.2 Далее осевая скорость постепенно уменьшается. Участок струи L’,на котором осевая скорость V ; эта область образует так называемое ядро струи. На граничных линиях ON и ON’ продольные скорости равны нулю; эти линии пересекаются на оси в точке О, называемой «полюсом».Изотахи- линии, проведенные через концы векторов, обозначающих равные скорости (линии равных скоростей). Если в пределах струи между указанными граничными линиями ON и ON’ построить изотахи то они образуют систему линий, напоминающих собой пламя свечи или газовой горелки. Эту систему, построенную в относительных координатах ( как U/V - отношение абсолютной скорости к скорости в выходном отверстии), называют факелом, а теорию поля в этой области – теорией факела. Эпюра абсолютных скоростей в каком- либо поперечном сечении основного участка струи шириной В, полученное опытным путем: рис.3 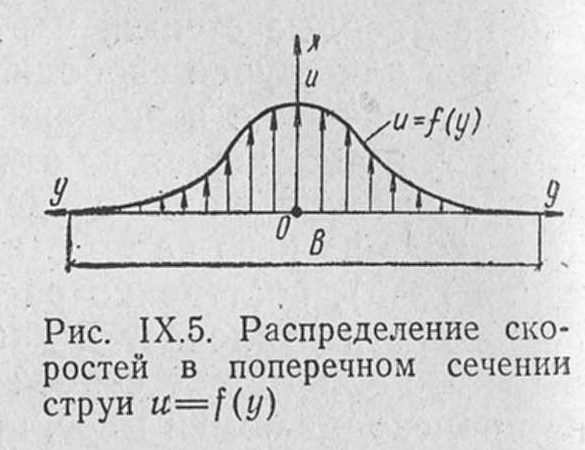 Если бы на одном и том же чертеже в одном и том же масштабе построить эпюры скоростей для ряда поперечных сечений основного участка, то получим следующую картину: рис.4 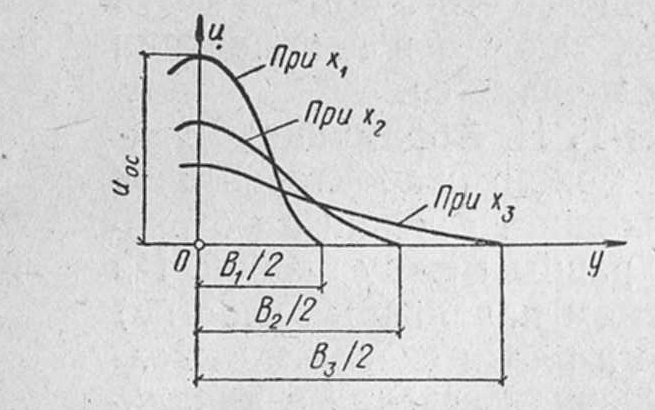 Изгиб воздушных струй Если температура струи отличается от температуры окружающего воздуха (tв 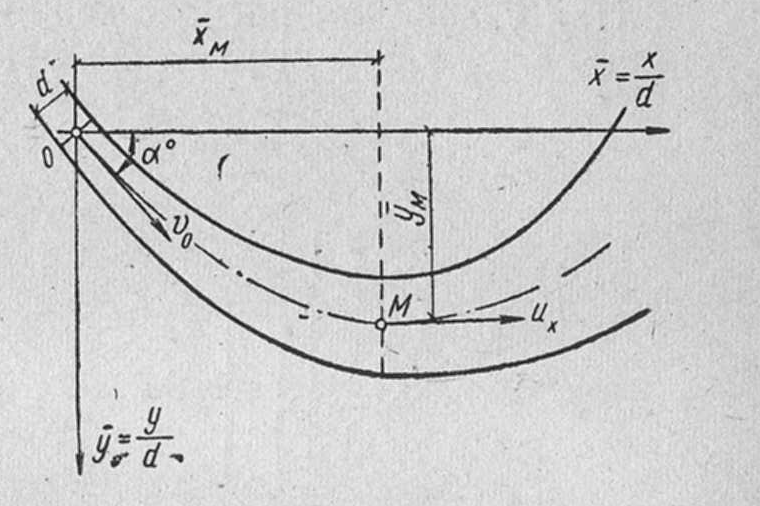 рис.5 Изгиб струи Уравнение осевой линии:  , где  =0,8- коэффициент турбулентности;  (здесь - начальная температура струи в  ;  - температура окружающего воздуха;  ).Координаты точки М (рис.5):  ; ; ;  и  ;  .При горизонтальном направлении скорости т.е. при   и  , и тогда уравнение осевой линии струи примет вид:  .Воздушная завеса. Теория воздушной струи по Г.Н.Абрамовичу широко используется при решении многих задач вентиляционной техники, в частности, при расчете «воздушной завесы». Как известно, для защиты производственных помещений от холодного наружного воздуха, поступающего через открытые ворота, применяется обдувка этих ворот струей теплого воздуха, который выходит из продольной щели, расположенной вдоль одной из сторон открытых ворот (рис.6). 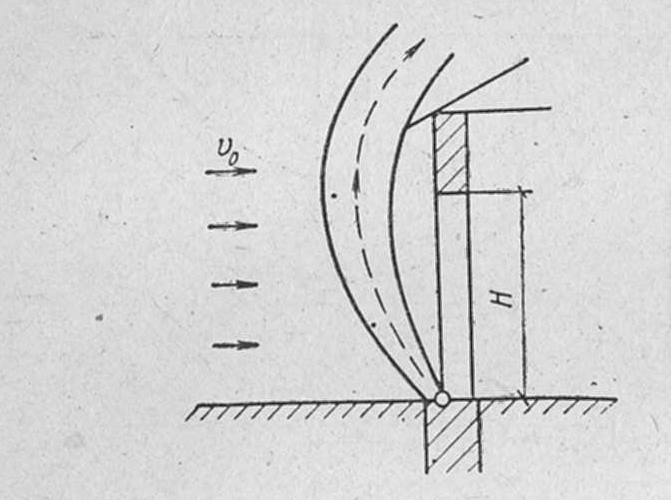 рис.6 Схема воздушной завесы ( Н-высота ворот). Пусть воздушная струя имеет осевую линию, образованную в итоге сложения двух движений: наружного воздуха со скоростью V 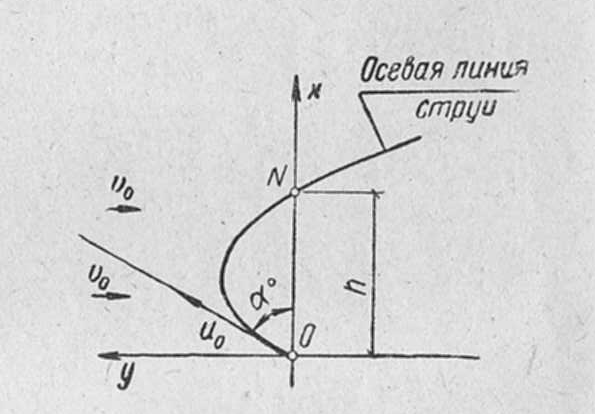, параллельной координатной оси oy (горизонтальной) и движения осевых частиц струи, выходящей под углом к вертикальной оси координат (оси ox). Осевая линия струи, отклоняясь от начального направления, пересекает ось ox в точке N ( рис.7). Очевидно, что если координата точки N (x=h) будет больше высоты H, то наружный воздух не войдет в ворота. Таким образом, задача сводится к определению величины начальной скорости V и угла , при которых h>H.Задача решается методом сложения потенциальных потоков. Потенциальный поток – безвихревой, не имеющий разрывов, поток невязкой жидкости, обладающий потенциалом скорости. На базе метода сложения потенциальных потоков Г.Н.Абрамович разработал критические инженерные методы расчета тепловых завес. Чтобы тепловая завеса выполняла свои функции необходимо, чтобы в точке N ее координаты (x=h, y=0) отвечали выражению так называемой «характеристики завесы»:  , где H, b- соответственно высота и ширина ворот, а Ф- функция, определяемая по формуле:  .С другой стороны, «характеристика завесы»- это:  , где  - приток наружного воздуха через ворота при бездействии завесы ( );  - приток наружного воздуха при работе завесы;  - расход воздуха в щели.Таким образом, при заданных значениях U , H, b: и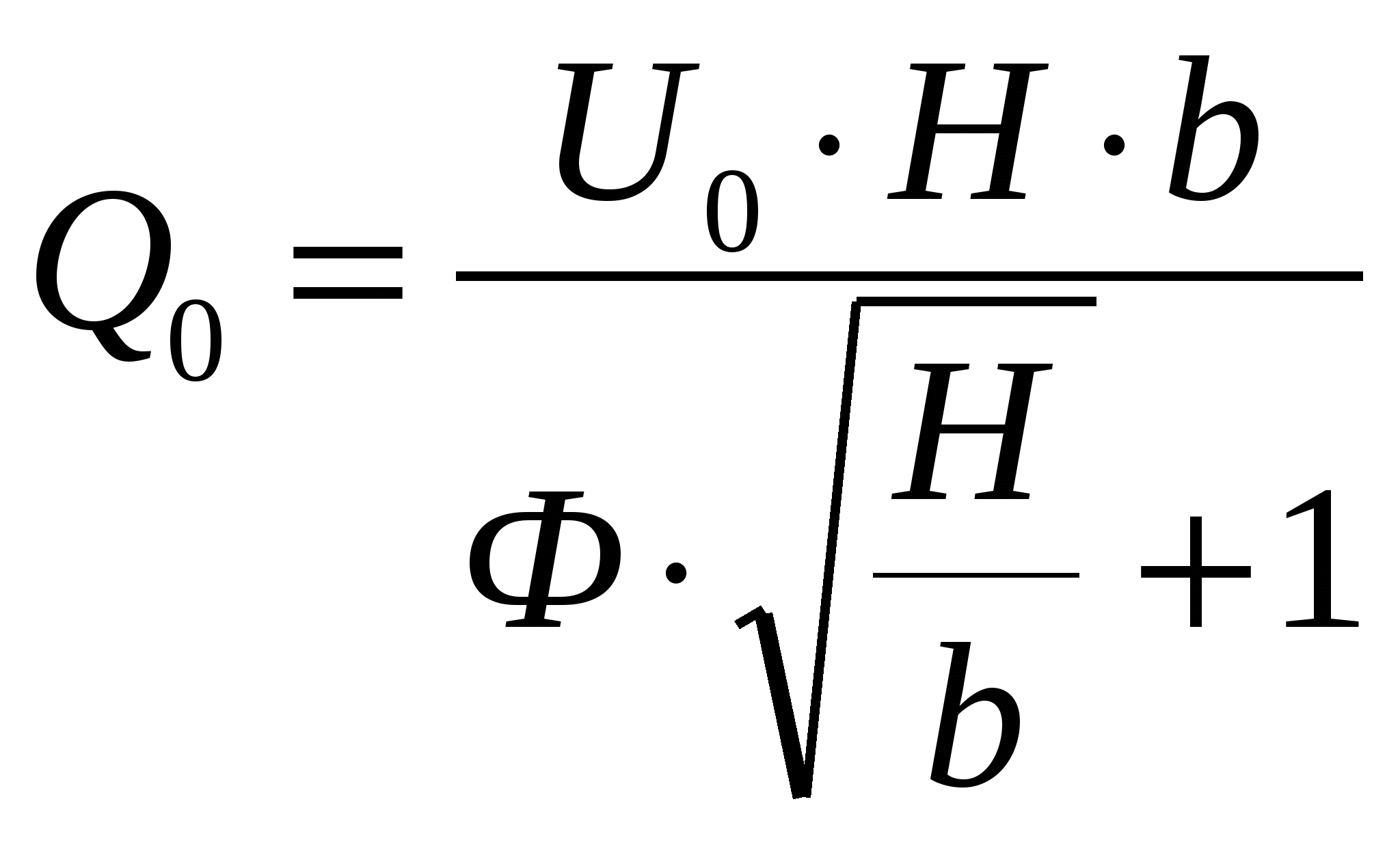ли  .По найденному расходу воздуха в щели рассчитывают параметры подводящего воздухопровода. Лопостные насосы Гидравлические машины. Гидромашины   насосы гидродвигатели Гидравлические машины, придающие протекающей через них жидкости дополнительную энергию – насосы. Гидравлические машины, отбирающие у движущейся жидкости часть энергию и превращающие ее в механическую работу – гидродвигатели. К гидравлическим машинам относят также гидравлические передачи и приводы. Классификация гидромашин по принципу действия. Гидромашины (насосы и т.д.) различают на динамические и объемные. Принцип действия динамических машин основан на аэро-гидродинамическом воздействии потока жидкости с лопатками рабочих колес этих машин. Принцип действия объемных машин основан на попеременном заполнении жидкостью (воздухом) пространства внутри машин – рабочей камеры с последующим вытеснением ее из рабочей камеры с помощью вытеснителя. Гидромашины динамического типа: турбина ГЭС. Объемные гидромашины – гидроцилиндр с вовратно–поступательным движением второго звена; гидромотор. Насосы. ∆Е = Ее-Е1  удельная энергия жидкости на входе и выходе.∆Е = (z2-z1) + (p2-p1)/ρg + (V22-V12)/2g Насосы могут обеспечивать приращение разных величин
Рабочие параметры насосов:
[Q] = [м3/с] – объемные [Qm] = [кг/с] – массовые
[∆H] =H2-H1 [м] (на выходе – на входе) 3) Давление насоса рн рн = Нρg Характеристики насоса: Н 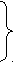 н = f (Qн) – напор показанные на графику зависимости -Nн = f (Q) – характеристики насоса, n = сonst (частота врвщения) ηm = f (Q) – к.п.д. НСТ=(z2-z1) + (p2-p1)/ρg Решение согласованной работы – рабочая точка. р = (р2-р1) + (v22-v12)/2g p ≡ p2-p1 4) мощность Nн – мощность, подводимая к насосу от двигателя – привода Nн.пол – полезная мощность Nн.пол = γθНн γ = ρg θφ = m – в единицу секунды от насоса подающего N = mgH – потенциальная энергия тела, поднятого на высоту Н. 1 сек насос подает Q жидкости. 5) КПД насоса ηн = Nн.пол/Nн<1 ηн = ηмах Насосная установка и ее характеристики.
 НасосыДинамические объемные По типу движения раб. органа Лопастные Струйные Возвратно- роторные Центробежные поступательный роторно- роторно- Вращательные поступательные осевые поршневые пинципные шестерные шиберные актально- диафражение (пластические) поршневые винтовые радиально- с наклонным поршневые блоком однократного и с наклонным двукратного диском действия Трубопровод от р.р. до Н – всасывающий участок трубопровода От Н до ПР – напорный трубопровод ПР, РР – может быть кА закрытым, так и закрытым./бак под ратм – открыт) Составим уравнение Бернулли для истечения жидкости/2 уровня от рр до Н и от Н до ПР ∆z = (z3-z0) 0-0 1-1 выед Д z0=0 z1 p0=p0 p1 V0=0 V1 ∑h 0-1 участок всасывания трубы р0/ρg = z1+p1/ρg+αV12/2g+∑hle – труб. ∆Н относится к самому насосу. Н относится к установке. 2-2 – выход ЭД 3-3 ∆z + ∆р/ρg – не зависит от Q – z2 z3 = ∆z статический напор, чтобы преодолеть p2 p3 разность уровня и давлений V2 V3 = 0
z2 + p2/ρg + αV22/2g = ∆z + p3/ρg + ∑hнапр. тр. ∆Н = Е2 – Е1 = z2 – z1 + (p2 – p1)1g + (V22 – V12)/2g (напор насоса) Е1 = р0/ρg - ∑hВС – из 0-1 Е2 = ∆z + p3 + ∑hHтр – из 2-3 Hпотреб = ∆z + p3/ρg + ∑hНтр – р0/ρg + ∑hВСтр = ∆z + (p3 – p0)/ρg + ∑hНтр + ∑hВСтр = = ∆z + (p3 – p0)/ρg + ∑hобщ Основы устройства и теория центробежного насоса(ЦН). |