Лекции по гидравлике (Полная версия). Техническая аэрогидродинамика

• Название: Техническая аэрогидродинамика
• Анкор: Лекции по гидравлике (Полная версия).doc
• Дата: 08.05.2017
• Размер: 6.88 Mb.
• Имя файла: Лекции по гидравлике (Полная версия).doc
• Тип: Документы; #7318
• страница: 4 из 4

Устройство и принцип действия (рабочий процесс)ЦН. Основными конструктивными элементами ЦН (рис.2.-1) являются: 1–рабочее колесо (РК); 2–вал РК; 3–корпус; 4–отводной канал (спиралевидная камера); 5–входной патрубок; 6–выходной патрубок (диффузор); 7–всасывающий трубопровод (В_сТ); 8–фильтр-сетка; 9–обратный клапан (КО); 10–напорный трубопровод (Н_пТ); 11–задвижка запорно-регулирующая (ЗРЗ); 12–заливное отверстие с крышкой; 13–расходный резервуар (РР).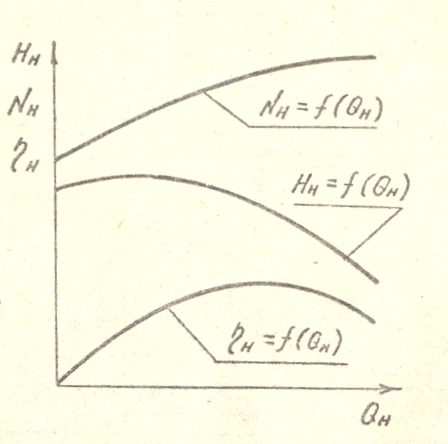

Рабочий процесс. ЦН не обладает способностью к самовсасыванию Ж из резервуара, расположенного ниже уровня входного отверстия. Поэтому перед пуском Н и В_сТ заливается Ж. При этом КО препятствует ее вытеканию в РР. Пуск ЦН производится при закрытой задвижке, постепенно открывающейся после достижения устойчивой частоты вращения РК. Его лопасти вращаясь, захватывают Ж, которая под действием центробежных сил начинает двигаться по межлопастным каналам от его центра к периферии, поступает в отводной канал и далее – в Н_пТ. Уходящая Ж освобождает пространство, в котором образуется вакуум, на РК поступает новая порция Ж и т.д.

При ГИД взаимодействии лопаток РК с Ж происходит преобразование механической энергии двигателя-привода в потенциальную и кинетическую энергию потока Ж.

Классификация ЦН. Прорабатывается самостоятельно по [2] стр. 207–209; [3] стр……

Характеристики ЦН.При проектировании насосных установок инженерам необходимо знать зависимости напора насоса, мощности и к.п.д. от его подачи, то есть функции Характер этих зависимостей зависит от частоты вращения рабочего колеса насоса n,плотности и вязкости Ж.

Будучи представленными в виде графиков при условии эти зависимости называются характеристиками насоса. Первая, наиболее важная из них, называется напорной характеристикой насоса.

Основное уравнение ЦН (ОУЦН). Точно рассчитать и построить характеристики насоса практически невозможно. Но об основных закономерностях напорной характеристики можно судить по ОУЦН, вывод которого, выполненный Л. Эйлером, составляет суть теории ЦН.

Допущения: 1. Рабочее колесо ЦН имеет бесконечное число лопастей . 2. Толщина каждой лопасти стремится к нулю, то есть траектории движения частиц Ж – бесконечное множество тонких линий, воспроизводящих очертания контура лопасти. 3. Насос считается совершенной машиной с . 4. Насос перекачивает идеальную жидкость, поэтому Такой насос называется идеальным, а его напор–теоретическим.

Движение Ж в рабочем колесе ЦН (рис.2-2). Каждая частица Ж, попадая на лопатку рабочего колеса ЦН в точке 1 (точке входа) совершает сложное движение, состоящее из вращения с угловой скоростью , и 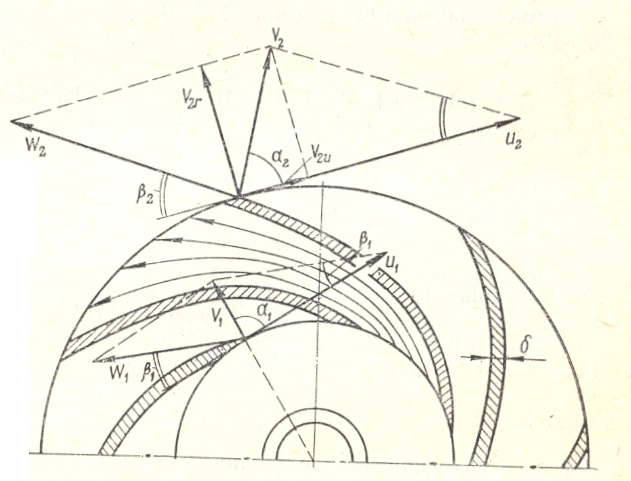поступательного перемещения частицы от точки входа к точке выхода (точка 2). Соответственно различают: 1. Скорость переносного движения (окружную скорость ), направленную по касательной к окружностям большого и малого радиусов в сторону вращения колеса; 2. Скорость относительного движения W, то естьскорость движения частиц Ж относительно лопастей рабочего колеса, направленную по касательной к лопасти; 3. Скорость абсолютного движения V, равную суммевекторов скоростей переменного и относительного движений .

На рис.2-2 изображены параллелограммы скоростей при входе на лопасть рабочего колеса и при выходе с лопасти . Там же показаны и –углы между абсолютной и окружной скоростями при входе на лопасть и выходе на колеса соответственно; углы и между относительной скоростью и отрицательным направлением окружной скорости при входе и выходе из колеса; радиальная и окружная составляющие абсолютной скорости на выходе , (2.1)и определяют форму лопастей, называются углами отгибки лопастей.

Величина теоретического напора может быть получена на основании теоремы гидромеханики о моменте количества движения Ж в равномерно вращающемся канале [1] стр. 152–153: «Приращение момента количества движения Ж в равномерно вращающемся канале M равно моменту М_ВН действующих на нее внешних сил» , т. е.M=М_ВН. (2.2)

В качестве М_ВН чаще всего выступает крутящий момент двигателя-привода (ДВС, электромотор, турбина и др. двигатели вращательного действия) крутящий момент которого определяется из уравнения баланса мощности подводимой к Н и его полезной мощности, т. е.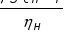




= (2.2)



В нашем случае при = 1 получаем




= (2.3)
Приращение момента количества движения Ж равно

M= (2.4)

Подставляя (2.3) и (2.4) в (2.2) и имея в виду, что в ЦН Ж обычно входит на рабочее колесо в радиальном направлении, то есть , а , получаем ОУЦН:

= = (2.5)
Влияние угла отгибки лопасти.

Преобразуем уравнение (2.5) так, чтобы напор выражался как функция расхода Q и размеров колеса. Расход жидкости через колесо выразим через радиальную составляющую абсолютной скорости на выходе из колеса и площадь выходного сечения:

= , откуда = (2.6)

Подставив это выражение в формулу (2.1) получим



=

тогда теоретический напор насоса будет равен: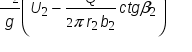



= (2.7)



Уравнение (2.7) позволяет построить напорную характеристику насоса

T =f(Q) при n =const (следовательно, U2=const). Как видно из выражения (2.7), характеристика такого насоса представляет собой прямую линию, наклон которой зависит от значения угла 2. Здесь следует различать три случая (рис.2.3):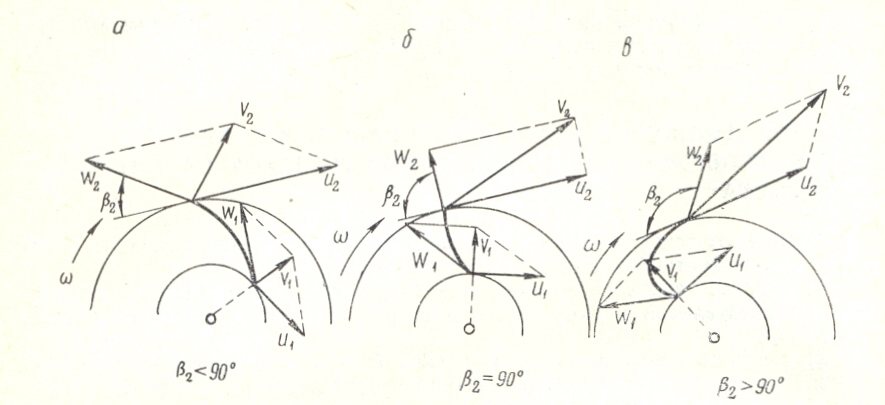



Рис.2.3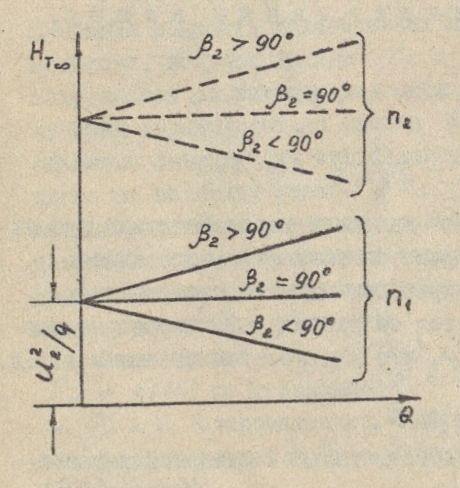

• 
  Лопасти отогнуты назад (290,
  

ctg290), напор с увеличением расхода А

уменьшается; рис.2.4

• 
  Лопасти имеют радиальный выход
  

(2=90, ctg2=0), напор не зависит от

расхода и равен


T =

• 
  Лопасти загнуты вперед (290,
  

ctg2<0), напор с увеличением расхода

увеличивается.

Соответствующие напорные характеристики идеального насоса показаны на рисунке 2.4.

Таким образом, наибольший теоретический напор создается насосом при отогнутых в направлении вращения лопастях. Однако, на практике предпочтение отдается насосам, РК которых имеет лопасти, отогнутые в сторону, противоположную вращению.

При изменении частоты вращения рабочего колеса напорная характеристика идеального насоса перемещается вдоль вертикальной оси, не меняя угол наклона. На рисунке 2.4 штриховыми линиями изображены характеристики при n2>n1.

Действительные характеристики насоса.
Рабочие органы насоса рассчитывают для определения сочетания подачи, напора и частоты вращения, причём размеры и форму проточной полости выбирают так, чтобы гидравлические потери при работе на этом режиме были минимальными. Такое сочетание подачи, напора и частоты вращения называется расчётным режимом. При эксплуатации насос может работать на режимах, отличных от расчётного. Так, прикрывая задвижку, установленную на напорном трубопроводе насоса, уменьшают подачу. При этом также изменяется напор, развиваемый насосом. Для правильной эксплуатации насоса необходимо знать, как изменяются напор, КПД и мощность, потребляемая насосом, при изменении его подачи, т.е. знать характеристику насоса, под которой понимается зависимость напора, мощности и КПД от подачи насоса при постоянной частоте вращения.

Действительный напор насоса будет меньше теоретического вследствие конечного числа лопастей и затрат энергии жидкости на преодоление гидравлических сопротивлений в самом насосе.

Влияние первого фактора проявляется в неравномерном распределении скоростей в сечениях межлопастных каналов, что приводит к уменьшению напора, развиваемого насосом. Конечное число лопастей учитывается введением поправочного коэффициента k_Z<1: H_TZ= k_ZH_T∞ , где H_TZ- теоретический напор насоса с конечным числом лопастей. Среднее значение коэффициента k_Z=0,8.

Потери напора ∆H_Г на преодоление гидравлических сопротивлений внутри насоса учитываются гидравлическим к.п.д. η_г, величина которого зависит от конструкции насоса и режима его работы и колеблется в пределах 0,85÷0,95.

Таким образом, действительный напор, развиваемый насосом,

H_H = H_TZ-∆H_Г = η_ГH_TZ = k_Z η_ГH_T∞, или H_H = k_Z η_Г

На рис. Показан переход от напорной характеристики идеального насоса H_T∞ = f(Q) к характеристике реального насоса H_H= f(Q_H), основанный на приведённых рассуждениях.

Подача насоса Q_H отличается от расхода Q через рабочее колесо на величину утечек ∆Q_У, что учитывается объёмным к.п.д. насоса η₀:

Q_H = Q-∆Q_У = η₀Q. Учёт утечек приводит к сдвигу действительной напорной характеристики насоса H_H = f(Q_H) относительно кривой H_H = f(Q) влево на величину ∆Q_У.

Построим кривую мощности насоса. Гидравлическая мощность насоса (мощность, сообщаемая жидкости в рабочем колесе без учёта объёмных и гидравлических потерь) равна N_Г = ρqQH_TZ. Зависимость теоретического напора H_TZ от расхода через рабочее колесо линейная и может быть выражена уравнением H_TZ = A-BQ (рис.2.5). Отсюда гидравлическая мощность N_Г = ρq(AQ-BQ²). Это уравнение параболы, пересекающей ось абсцисс в точках Q=0 и Q=A/B (кривая N_Г = f(Q) на рис.2.6 ).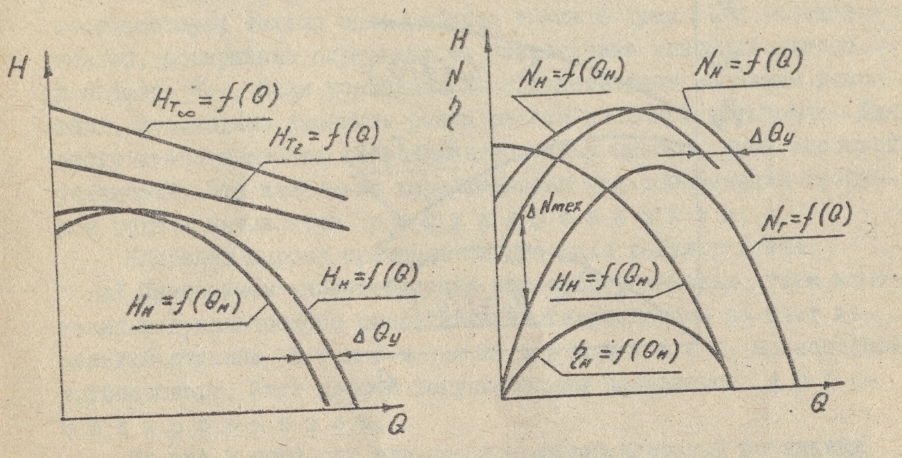



рис.2.5 рис.2.6

Прибавив мощность механических потерь ∆N_МЕХ к гидравлической мощности, получим кривую N_H = f(Q) зависимости мощности на валу насоса от расхода жидкости через рабочее колесо. Для получения характеристики насоса N_H = f(Q) остаётся учесть объёмные потери. Для этого кривую N_H = f(Q) нужно сместить влево на величину утечек ∆Q_У. Из рис. Видно, что минимальная потребляемая мощность соответствует режиму насоса при Q=0, поэтому пуск центробежного насоса производится при закрытой задвижке на напорном трубопроводе, чтобы уменьшить пусковую мощность приводящего двигателя.

Имея кривые N_H = f(Q) и H_H = f(Q_H), построим кривую η_H = f(Q_H) по уравнению η_H = ρgQ_HH_H/N_H. При Q_H=0 и H_H=0 → η_H=0. Следовательно, кривая к.п.д. пересечёт ось абсцисс в начале координат (Q_H=0) и в точке, где её пересекает кривая напора.

Данные рассуждения являются приближёнными, так как не учитывают ряда факторов, влияющих на напор и мощность. Поэтому характеристики насоса, построенные теоретически на основе описанных формул, плохо согласуется с данными опыта. С достаточной для практики точностью характеристики насоса могут быть получены лишь опытным путём.

Характеристика центробежного насоса представляет графическое изображение зависимости напора Н , мощности N, к.п.д. η и допускаемой вакуумметрической высоты всасывания Нвак от подачи насоса Q при постоянных значениях частоты вращения РК n и плотности Ж на входе в насос. При другой частоте вращения РК n1 характеристика насоса может быть пересчитана по формулам :

= , = , =

.

На рис.2.7 приведены кривые связи H-Q иN-Q при различной частоте вращения РК, называемые универсальными или топографическими характеристиками. Кроме того, на рисунке нанесены кривые напора Н

( нисходящие линии ) и мощности N ( восходящие линии ) в функции от подачи Q. С помощью таких графиков можно для данной марки насоса выявить значения Q, H, Nи η при различной частоте вращения РК.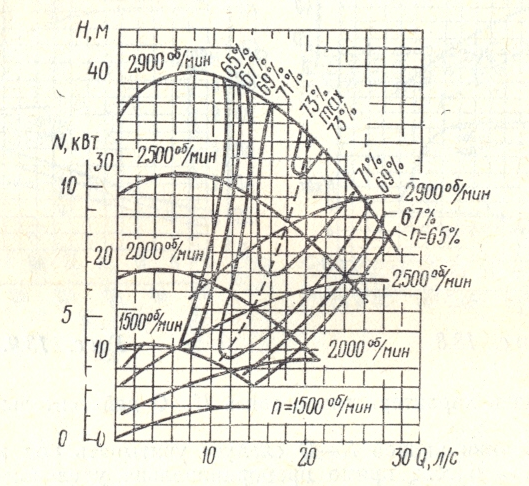


рис.2.7