Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистик. Тема Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистики
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
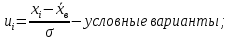 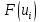 – значения функции Лапласа; – значения функции Лапласа;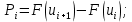 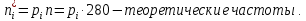 Согласно критерию Пирсона получаем значение 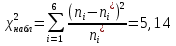 По таблице критических значений 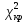 при уровне значимости α=0,05 и числе степеней свободы k=l−3=6−3=3 находим при уровне значимости α=0,05 и числе степеней свободы k=l−3=6−3=3 находим 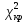 ≈7,81. Так как ≈7,81. Так как 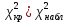 гипотеза о нормальном распределении при выбранном уровне значимости принимается. гипотеза о нормальном распределении при выбранном уровне значимости принимается.При уровне значимости α=0,01 и числе степеней свободы k=l−3=6−3=3 значение 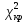 ≈11,3. Сравнив его с вычисленным значением статистики Пирсона при выбранном уровне значимости отвергается. ≈11,3. Сравнив его с вычисленным значением статистики Пирсона при выбранном уровне значимости отвергается.1.3. Доверительный интервал для математического ожидания имеет вид 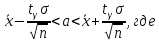 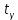 – коэффициент, находимый по таблице значений функции Лапласа. Согласно этой таблице для надежности – коэффициент, находимый по таблице значений функции Лапласа. Согласно этой таблице для надежности 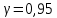 , коэффициент , коэффициент 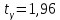 . Тогда точность оценки . Тогда точность оценки 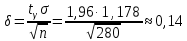 Таким образом, искомый доверительный интервал для математического ожидания 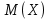 равен (-0,163; 0,117). равен (-0,163; 0,117).Доверительный интервал для оценки неизвестной дисперсии имеет вид 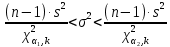 χ2 – хи-квадрат распределение, а его критические значения 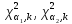 значения вычисляются по значениям значения вычисляются по значениям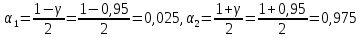 По таблице критических значений хи-квадрат распределения для 1, 2 и числа степеней свободы k=n-1=280-1=279 находим 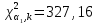 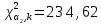 Доверительный интервал для оценки неизвестной дисперсии 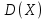 равен равен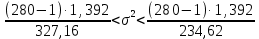 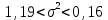 2. Проверим гипотезу, значимо ли отличается средний показатель совокупности от некоторого заданного значения 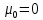 при помощи t-критерий Стьюдента. Критические значения критерия, соответственно выбранному уровню значимости α и степени свободы v найдем по таблице значений критерия Стьюдента. при помощи t-критерий Стьюдента. Критические значения критерия, соответственно выбранному уровню значимости α и степени свободы v найдем по таблице значений критерия Стьюдента.Вычисляемое значение критерия 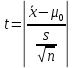 где среднее выборки, 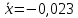 некоторое заданное среднее значение, 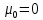 ; ;s стандартное отклонение, s=1,18; n мощность выборки, n=280; 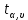 критическое значение t-критерия Стьюдента, критическое значение t-критерия Стьюдента, 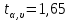 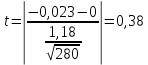 Так как 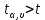 , то есть фактическое значение статистического критерия меньше критического значения, то фактическое значение попадает в область принятия гипотезы. , то есть фактическое значение статистического критерия меньше критического значения, то фактическое значение попадает в область принятия гипотезы.3. Выберем из заданной в варианте выборки первые три и три последних столбцов и будем считать их независимыми выборками наблюдениями за С.В. 𝝃 и 𝜼 соответственно.
|
