Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистик. Тема Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистики
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
2) Найдем условные законы распределения случайной величины от значений реализаций СВ по формуле 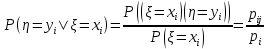 Условные распределения случайной величины при условии, что ={1; 3; 4} приведем в виде таблицы 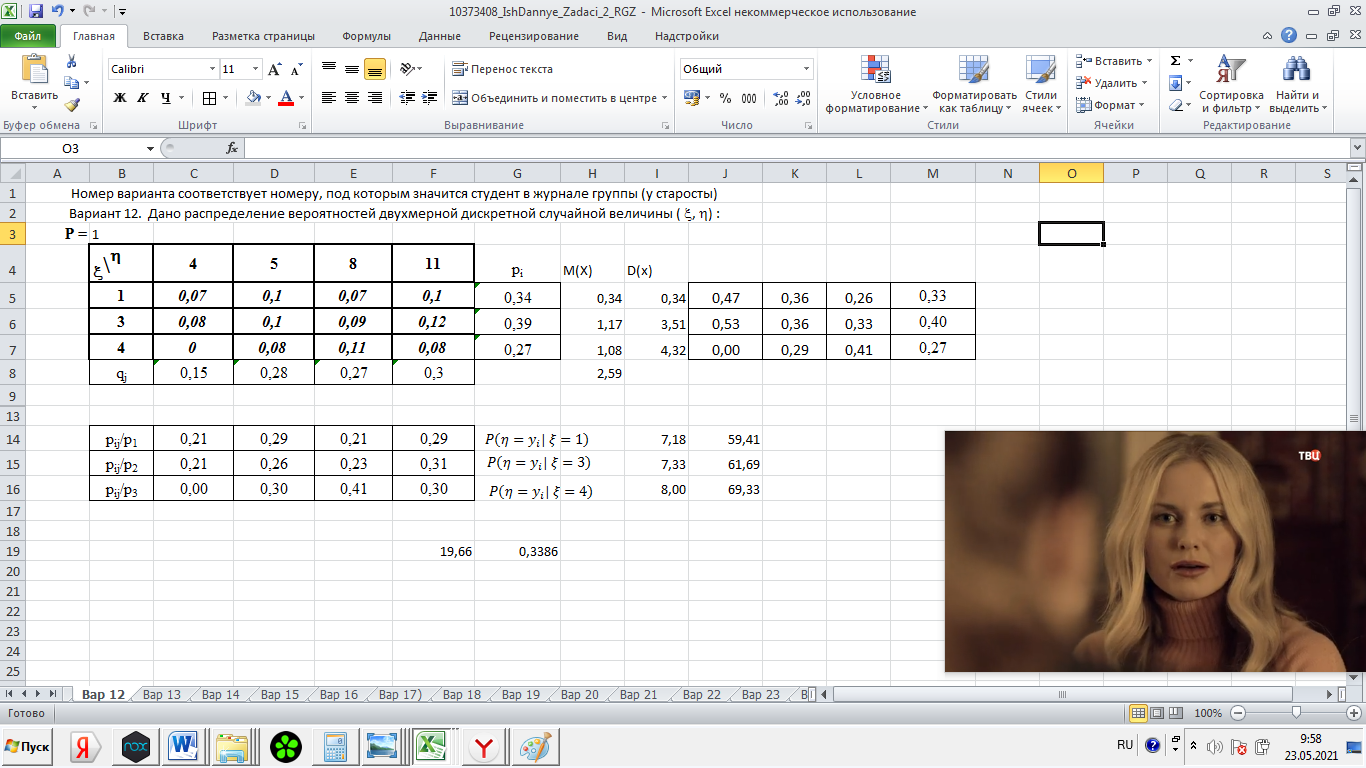 Условные математические ожидания равны 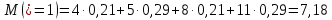 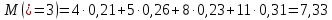 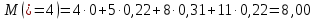 Условные дисперсии принимают значения 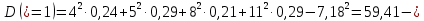 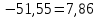 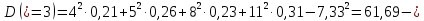 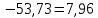 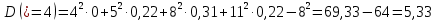 Условные среднеквадратичные отклонения равны 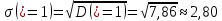 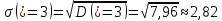 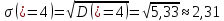 3) Выполним построения графическое изображение совместного закона распределения двухмерной СВ в виде диаграммы рассеивания. 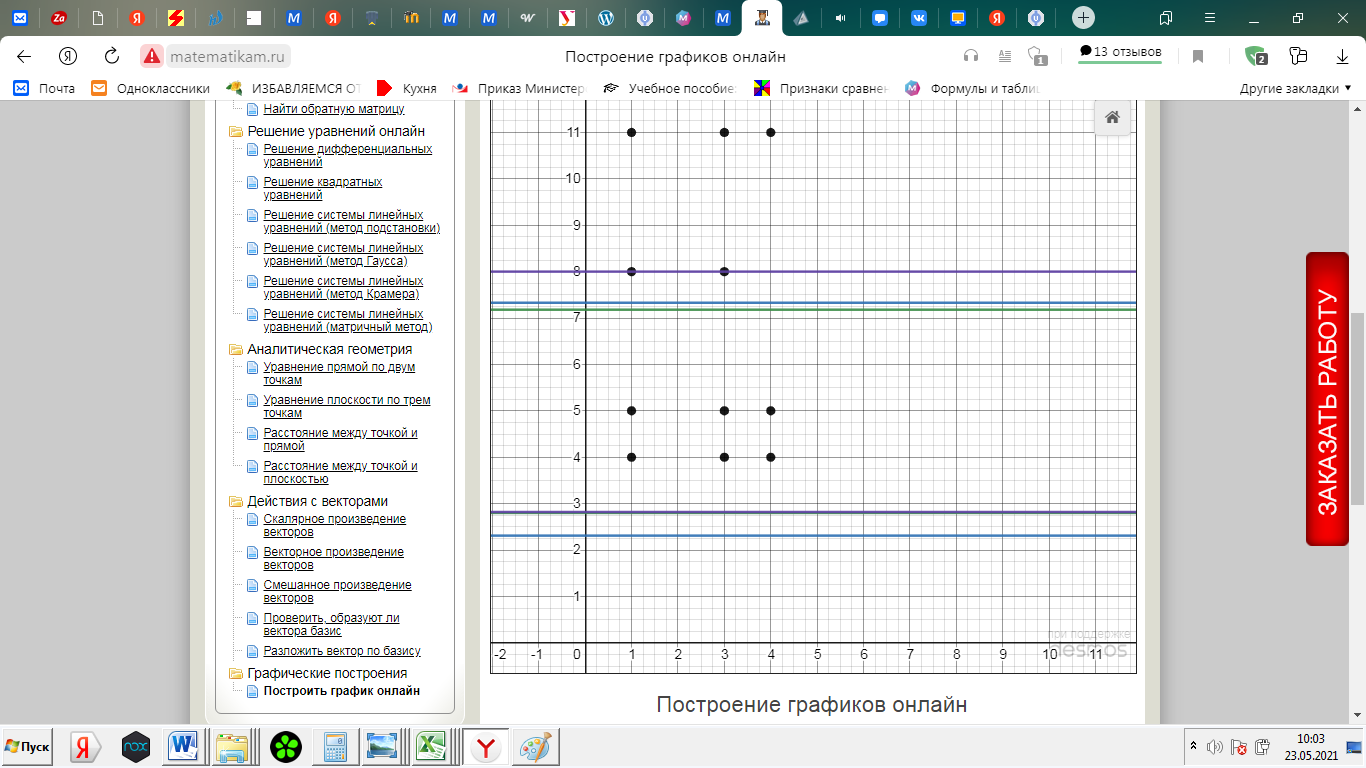 4) Определим ковариацию, корреляцию, генеральное корреляционное отношение, функцию линейной регрессии и построить её график, совмещенный с графиками условного математического ожиданий и условного среднеквадратичного отклонения СВ | {=xi}. Ковариация двухмерной случайной величины равна 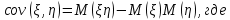 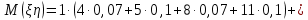 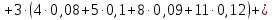 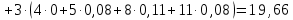 Тогда ковариация равна 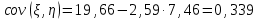 Коэффициент корреляции находится по формуле  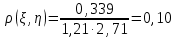 Выборочное уравнение линейной регрессии на имеет вид 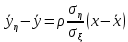 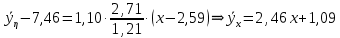 Построим график функции по найденному уравнению: 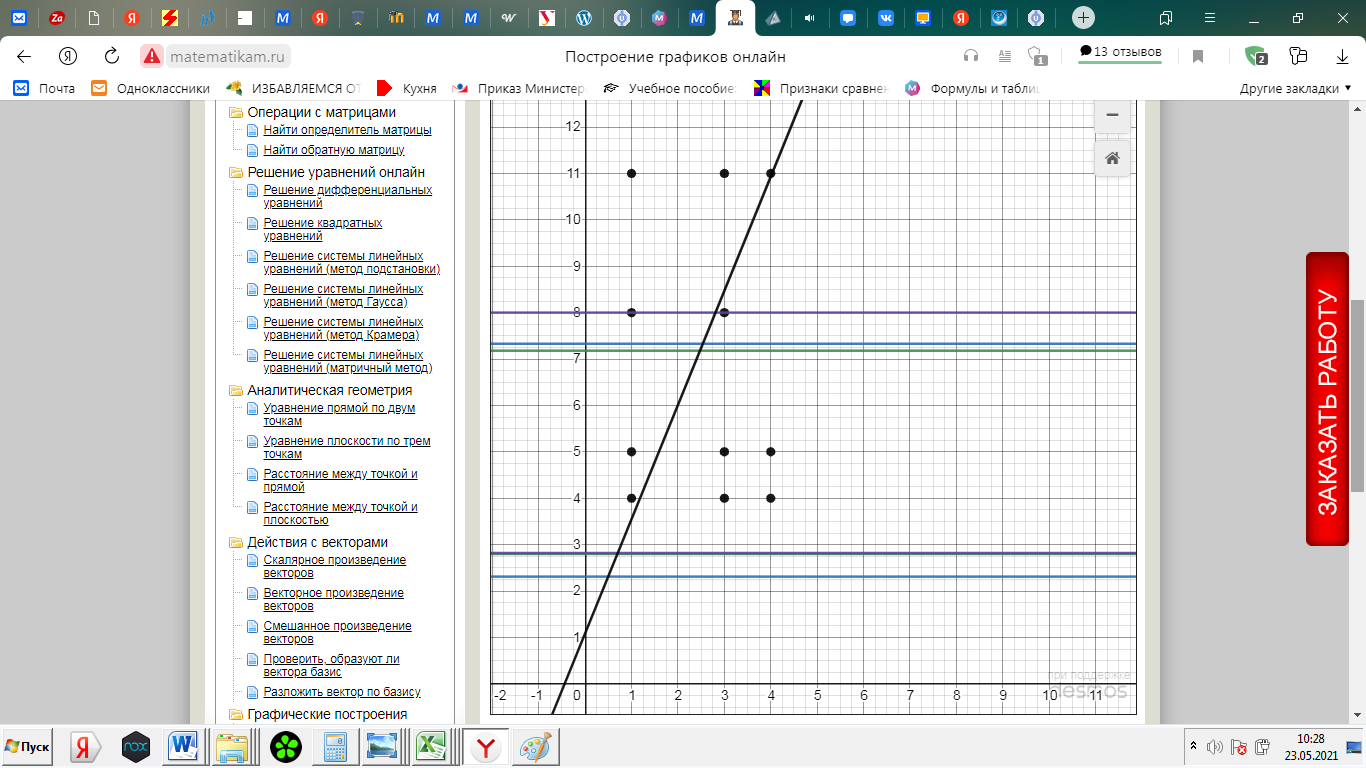 Задача 3. Дана выборка из непрерывной генеральной совокупности. Требуется: 1. «Восстановить» распределение генеральной совокупности 1.1. Подготовить исходные данные (выборку) к виду, удобному для обработки и анализа статистических данных задания в табличной и графической форме. 1.1.1. Описать выборку в виде вариационного, статистического и вероятностных рядов разного типа. 1.1.2. Представить выборку в графической форме (полигоном, гистограммой, круговой диаграммой, кумулятивной кривой и т.д. , но не менее 5 видов графиков выборки). 1.1.3. Вычислить не менее 10 описательных статистик: характеристик центра, рассеивания, коэффициенты формы выборочного распределения выборки и т.д. 1.2. Провести анализ полученных результатов описания выборки: выдвинуть и проверить гипотезу о законе распределения теоретической случайной величины. 1.2.1. Оценить параметры гипотетического распределения. 1.2.2. Построить на одном рисунке графики выборочного и гипотетического закона распределения и оценить степень сходства (различия) между ними. 1.2.3. Проверить по выбранному критерию согласия выдвинутую гипотезу о распределении наблюдаемой случайной величины на 5% уровне значимости. Что изменится, если уровень значимости 1%? 1.3. Оценить качество оценок параметров закона распределения генеральной совокупности. 1.3.1. Определить погрешность в вычислении параметров (хотя бы одного параметра) распределения за счет группировки исходной выборки. 1.3.2. Построить 95% доверительные интервалы для параметров (параметра) «теоретического» распределения. 2. Сформулировать и проверить на выбранном (5% уровне) значимости не менее 3 статистических гипотез (по выбору студента) о параметрах и свойствах исследуемой выборки генеральной совокупности. 3. Выберем из заданной в варианте выборки первые три и три последних столбцов и будем считать их независимыми выборками - наблюдениями за С.В. 𝝃 и 𝜼 соответственно. 3.1. Проверить гипотезу об однородности этих выборок. 3.2. Проверить гипотезу о равенстве средних 𝝃 и 𝜼. 3.3. Построить диаграмму рассеяния величин (𝝃, 𝜼), вычислить выборочный коэффициент корреляции 𝝆(𝝃, 𝜼) и аппроксимировать зависимость между 𝝃 и 𝜼 прямой линией Исходные данные к задаче № 3.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
