Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистик. Тема Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистики

• Название: Тема Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистики
• Анкор: Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистик
• Дата: 27.06.2021
• Размер: 0.95 Mb.
• Имя файла: Р_Г_Р.docx
• Тип: Задача; #221912
• страница: 7 из 7

С помощью критерия Стьюдента проверим гипотезу об однородности выборок: математическое ожидание первой выборки незначимо отличается от математического ожидания второй выборки или .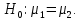

Критерий рассчитывается по формуле: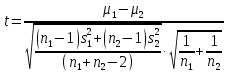



где μ1 и μ2  математические ожидания первой и второй выборок размерами n₁ и n₂ соответственно;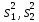

 дисперсии первой и второй выборок;

n1+n22 число степеней свободы.

Чем ближе значения критерия к нулю, тем больше вероятность, что основная гипотеза будет верной (при этом знак не имеет значения).

Найдем числовые характеристики величин с помощью процедуры Описательная статистика.

Х		У
Среднее	-1,392	Среднее	1,357
Стандартная ошибка	0,052	Стандартная ошибка	0,062
Медиана	-1,314	Медиана	1,248
Мода		Мода
Стандартное отклонение	0,475	Стандартное отклонение	0,567
Дисперсия выборки	0,226	Дисперсия выборки	0,321
Эксцесс	1,749	Эксцесс	1,301
Асимметричность	-1,142	Асимметричность	1,147
Интервал	2,280	Интервал	2,682
Минимум	-3,020	Минимум	0,667
Максимум	-0,741	Максимум	3,349
Сумма	-116,906	Сумма	114,006
Счет	84,000	Счет	84,000
Уровень надежности(95,0%)	0,103	Уровень надежности(95,0%)	0,123

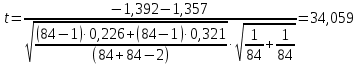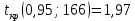Так как 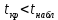гипотеза H₀ отвергается.

Выдвинем гипотезу 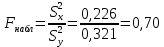при альтернативной гипотезе Рассчитаем значение статистики



По таблице критических значений при заданном уровне значимости и степенях свободы определим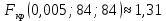



следовательно, гипотеза принимается.

Построиv диаграмму рассеяния величин (𝝃, 𝜼),

Вычислим выборочный коэффициент корреляции 𝝆(𝝃, 𝜼) и аппроксимируем зависимость между 𝝃 и 𝜼 прямой линией.

Тогда коэффициент линейной корреляции равен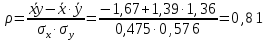



Полученное значение коэффициента корреляции говорит о наличии положительной (>0) сильной (r>0,7) корреляционной связи между рассматриваемыми величинами.

Выборочное уравнение линейной регрессии  на  имеет вид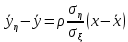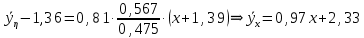




Заключение

Первичная обработка данных служит для содержательной интерпретации результатов произведенных вычислений.

1. Интерпретация .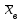

Среднее значение изучаемого признака (математическое ожидание).

2. Интерпретация Мо.

Наиболее часто встречаемое значение признака.

3. Интерпретация Ме.

Значение, которое делит изучаемую совокупность на равные части.

4. Интерпретация .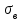

Отклонение времени отдельно взятого значения в среднем

5. Интерпретация R.

Амплитуда изменения значений признака, колеблется от 0 до 6 часов.

6. Интерпретация V.

Коэффициент вариации (> 33%) позволяет сделать вывод о неоднородности или однородности изучаемой совокупности.

7. Интерпретация As.

Коэффициент асимметрии характеризует скошенность распределения по отношению к математическому ожиданию. Если асимметрия положительна, то имеется правосторонняя асимметрия (более длинная ветвь направлена вправо).

7. Интерпретация Еs.

Отрицательное значение эксцесса указывает на низковершинное распределение.

8. Интерпретация Еs.

Коэффициент корреляции характеризует тесноту связи между изучаемыми признаками. Линейная корреляционная связь между случайными величинами сильная,если | r_в |>0,7.

Глоссарий

Варианта – элемент выборки.

Вариационный ряд – последовательность вариант, записанных в возрастающем (убывающем) порядке.

Выборка – совокупность случайно отобранных из изучаемой генеральной совокупности объектов.

Выборочный метод – оценка параметров (характеристик) генеральной совокупности по данным выборки.

Генеральная совокупность – вся подлежащая изучению совокупность объектов (наблюдений).

Гипотеза статистическая – предположение о распределении вероятностей наблюдаемой случайной величины.

Гистограмма – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы, а высоты равны частотам.

Группированный статистический ряд – ряд распределения, полученный на основе статистического ряда (выборки объема n) путем деления размаха выборки на k интервалов (групп).

Дисперсия (рассеяние) случайной величины – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Доверительный интервал – интервал, который покрывает неизвестный параметр с заданной надежностью.

Закон распределения случайной величины – всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Корреляционный анализ – исследование наличия (линейной) взаимосвязи между группами переменных.

Корреляционная зависимость – зависимость, при которой при изменении одной из величин изменяется среднее значение другой/

Коэффициент корреляции – отношение ковариации к произведению средних квадратических отклонений двух случайных величин.

Критерий согласия Пирсона (критерий  2 – «хи-квадрат») – критерий для проверки нулевой гипотезы о распределении случайной величины. Математическое ожидание – число, относительно которого стабилизируется среднее арифметическое возможных значений случайной величины при достаточно большом количестве испытаний.

Метод наименьших квадратов (МНК) – метод оценки параметров на основании экспериментальных данных, содержащих случайные ошибки. Несмещенная оценка – оценка, математическое ожидание которой равно оцениваемому параметру.

Нулевая гипотеза – основная выдвинутая гипотеза.

Полигон частот – ломаная линия, отрезки которой соединяют точки: значение и его частоту.

Размах варьирования R – разность между наибольшей и наименьшей вариантой. Ранжированный ряд – статистический ряд (выборка), в котором элементы расположены в порядке возрастания или убывания.

Регрессия – это функциональная зависимость между значениями одного из исследуемых признаков и условными средними значениями другого.

Ряд распределения – способ задания закона распределения вероятностей дискретной случайной величины, содержащий возможные значения этой величины и соответствующие им вероятности.

Среднее квадратическое отклонение (стандартное отклонение или стандарт) случайной величины – арифметическое значение корня квадратного из ее дисперсии.

Статистика – случайная величина, являющаяся функцией выборки.

Функция регрессии – форма связи генеральной совокупности значений переменных величин X и Y. В зависимости от вида функции регрессии связь между X и Y может быть линейной или нелинейной.

Частости, относительные частоты – отношение частот к общему числу наблюдений.

Частоты – числа, показывающие, сколько раз встречаются варианты из данного интервала.

Числовые характеристики случайной величины – математическое ожидание, дисперсия, среднее квадратическое отклонение и другие числа, призванные в сжатой форме выразить наиболее существенные черты распределения.

Эмпирическое распределение – распределение случайной величины, полученное на основе выборки.
Список использованной литературы

1. Балдин К.В. Теория вероятностей и математическая статистика: учебник/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев, - М.: Дашков и К, 2016. – 472 с.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие / В.Е. Гмурман. – М.: Высшая школа, 2008. – 404 с.

3. Ватутин В.А. Теория вероятностей и математическая статистика в задачах / В.А. Ватутин, Г.И. Ивченко, Ю.И. Медведев, - М.: Лененд, 2015, - 384 с.

4. Кацман Ю.Я. Теория вероятностей и математическая статистика. Примеры с решениями: учебное пособие для прикладного бакалавриата/ Ю.Я. Кацман. - Люберцы: Юрайт, 2016, - 130 с.

5. Горелова Т.В. Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с прменением Excel – Ростов н/Д: Феникс, 2005. – 480 с.