Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистик. Тема Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистики
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Расчетно-графическая работа по теории вероятностей и математической статистике ТЕМА: Анализ вероятностных свойств одномерных и двухмерных случайных величин средствами теории вероятностей и математической статистики Задание Задача 1. Пассажир может уехать на любом из двух маршрутов автобусов. Закон времени ожидания прихода этих автобусов задается графиком плотности распределения вероятности случайной величины . 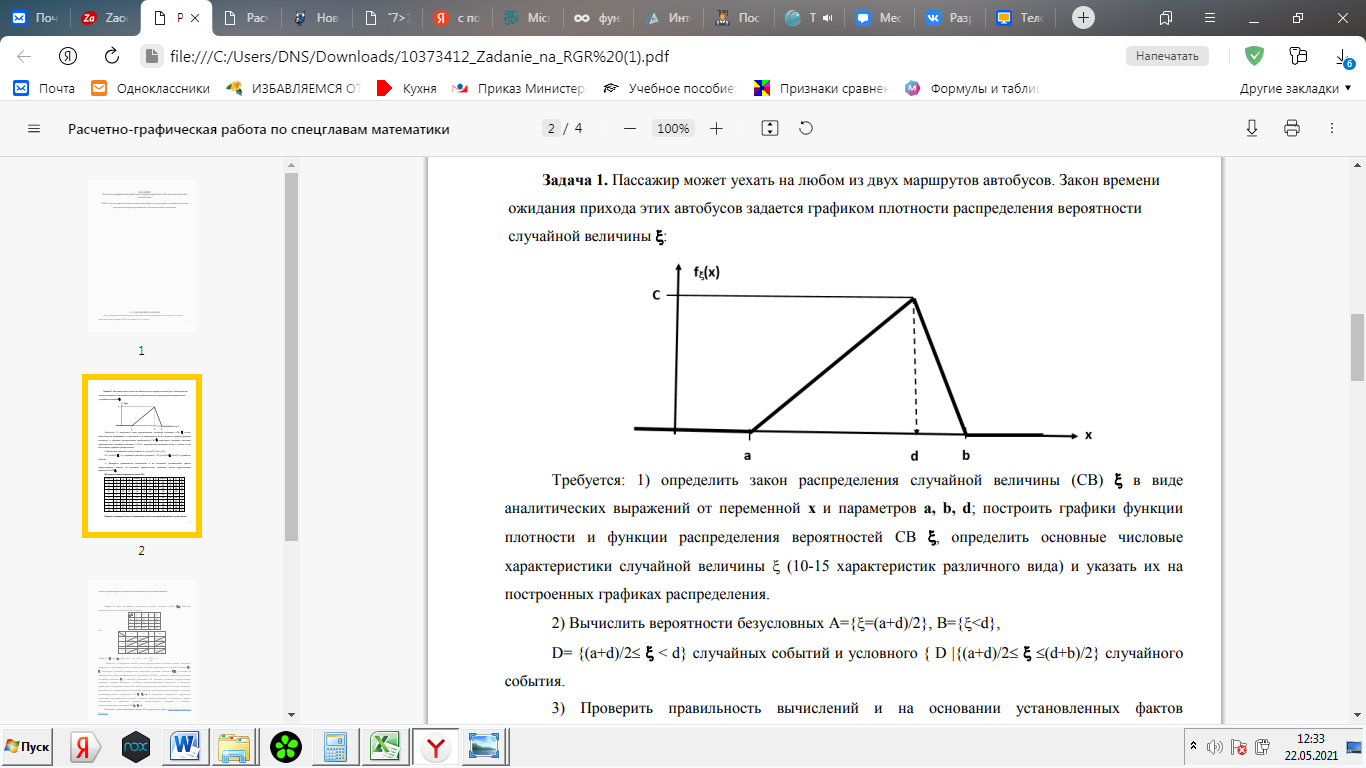 Требуется: 1) определить закон распределения случайной величины в виде аналитических выражений от переменной х и параметров а, b, d; построить графики функции плотности и функции распределения вероятностей случайной величины , определить основные числовые характеристики случайной величины (10-15 характеристик различного вида) и указать их на построенных графиках распределения. 2) Вычислить вероятности безусловных 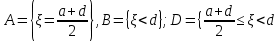 случайных событий и условного случайных событий и условного 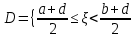 случайного события. случайного события.3) проверить правильность и на основании установленных фактов сформулировать выводы об основных вероятностных свойствах закона распределения вероятностей случайной величины . Задача 2. Дана двухмерная дискретная случайная величина 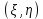 таблицей распределения в виде вероятностной матрицы. таблицей распределения в виде вероятностной матрицы.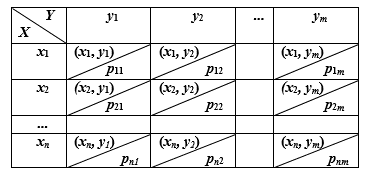 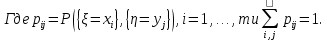 Требуется: 1) Определить частные законы распределения и основные (математическое ожидание, дисперсию и среднеквадратическое отклонение) числовые характеристики случайных величин и , совместную функцию распределения дискретной случайной величины (,) и вектора её характеристик центра распределения и рассеивания. 2) Найти условные законы распределения случайной величины от значений реализаций СВ, значения условного математического ожиданий, условной дисперсии, условного среднеквадратичного отклонения. 3) Построить графическое изображение совместного закона распределения двухмерной СВ в виде диаграммы рассеивания и наложенными на неё линями условного математического ожиданий и условного среднеквадратичного отклонения СВ | {=xi}. 4) Определить ковариацию, корреляцию, генеральное корреляционное отношение, функцию линейной регрессии и построить её график, совмещенный с графиками условного математического ожиданий и условного среднеквадратичного отклонения СВ | {=xi}. Задача 3. Дана выборка из непрерывной генеральной совокупности. Требуется: 1. «Восстановить» распределение генеральной совокупности 1.1. Подготовить исходные данные (выборку) к виду, удобному для обработки и анализа статистических данных задания в табличной и графической форме. 1.1.1. Описать выборку в виде вариационного, статистического и вероятностных рядов разного типа. 1.1.2. Представить выборку в графической форме (полигоном, гистограммой, круговой диаграммой, кумулятивной кривой и т.д. , но не менее 5 видов графиков выборки). 1.1.3. Вычислить не менее 10 описательных статистик: характеристик центра, рассеивания, коэффициенты формы выборочного распределения выборки и т.д. 1.2. Провести анализ полученных результатов описания выборки: выдвинуть и проверить гипотезу о законе распределения теоретической случайной величины. 1.2.1. Оценить параметры гипотетического распределения. 1.2.2. Построить на одном рисунке графики выборочного и гипотетического закона распределения и оценить степень сходства (различия) между ними. 1.2.3. Проверить по выбранному критерию согласия выдвинутую гипотезу о распределении наблюдаемой случайной величины на 5% уровне значимости. Что изменится, если уровень значимости 1%? 1.3. Оценить качество оценок параметров закона распределения генеральной совокупности. 1.3.1. Определить погрешность в вычислении параметров (хотя бы одного параметра) распределения за счет группировки исходной выборки. 1.3.2. Построить 95% доверительные интервалы для параметров (параметра) «теоретического» распределения. 2. Сформулировать и проверить на выбранном (5% уровне) значимости не менее 3 статистических гипотез (по выбору студента) о параметрах и свойствах исследуемой выборки генеральной совокупности. 3. Выберем из заданной в варианте выборки первые три и три последних столбцов и будем считать их независимыми выборками - наблюдениями за С.В. 𝝃 и 𝜼 соответственно. 3.1. Проверить гипотезу об однородности этих выборок. 3.2. Проверить гипотезу о равенстве средних 𝝃 и 𝜼. 3.3. Построить диаграмму рассеяния величин (𝝃, 𝜼), вычислить выборочный коэффициент корреляции 𝝆(𝝃, 𝜼) и аппроксимировать зависимость между 𝝃 и 𝜼 прямой линией Содержание 1. Введение 7 2. Основная часть 8 2.1. Задача 1 8 2.2. Задача 2 14 2.3. Задача 3 20 3. Заключение 35 4. Глоссарий 36 5. Список использованных источников 39 Введение Целью выполнения расчетно-графической работы по дисциплине теория вероятностей и математическая статистика является формирование представлений о методах и приемах обработки данных, обобщение знаний и применение математического аппарата. В процессе решения задач необходимо выработать умения применять выводы и положения теории вероятностей и математической статистики для решения практических задач; получить представления об общих вероятностных характеристиках изучаемых процессов и навыки самостоятельной работы с литературой. Использование основных понятий и характеристик изучаемых явлений, таких как вероятность, плотность распределения вероятностей, математическое ожидание, дисперсия и т.п. позволяет построить вероятностно-статистическую модель какого либо технического или экономического процесса, спрогнозировать его поведение и сделать вывод. Основная часть Задача 1. Пассажир может уехать на любом из двух маршрутов автобусов. Закон времени ожидания прихода этих автобусов задается графиком плотности распределения вероятности случайной величины .  Требуется: 1) определить закон распределения случайной величины в виде аналитических выражений от переменной х и параметров а, b, d; построить графики функции плотности и функции распределения вероятностей случайной величины , определить основные числовые характеристики случайной величины (10-15 характеристик различного вида) и указать их на построенных графиках распределения. 2) Вычислить вероятности безусловных 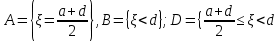 случайных событий и условного случайных событий и условного 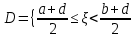 случайного события. случайного события.3) проверить правильность и на основании установленных фактов сформулировать выводы об основных вероятностных свойствах закона распределения вероятностей случайной величины . Исходные данные задачи №1.
Решение: 1) Определим аналитическое выражение закона распределения случайной величины для заданных значений параметров а, b, d. Составим уравнения прямых, проходящих через две заданные точки по формуле: 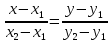 Отрезок прямой от точки (0; 0) до точки (4; с) имеет запись 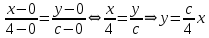 Отрезок прямой от точки (4; c) до точки (8; 0) имеет запись 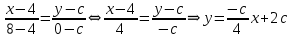 Таким образом, плотность распределения случайной величины равна 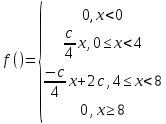 Найдем значение параметра с. Плотность распределения обладает свойством 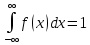 В нашем случае плотность определена на четырех промежутках, поэтому получим сумму четырех интегралов 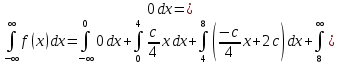 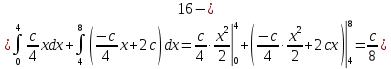 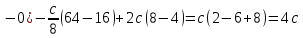 Получили уравнение 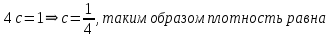 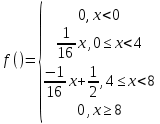 Составим функцию распределения F(x). 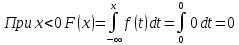 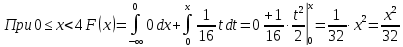 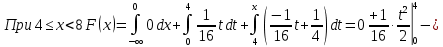 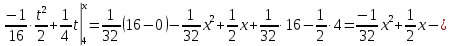 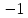 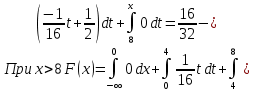 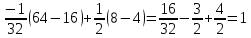 Таким образом, функция распределения имеет вид 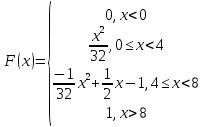 Построим графики функций (рис. 1). f(x) и F(x). 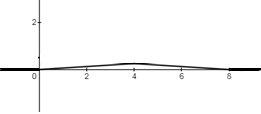 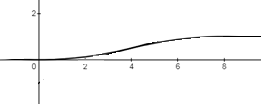 Рисунок 1. Графики функций распределения. Вычислим основные числовые характеристики случайной величины . 1. Математическое ожидание непрерывной случайной величины найдем по формуле 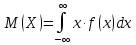 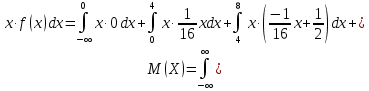 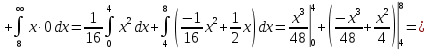 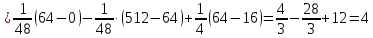 2. Дисперсию непрерывной случайной величины вычислим по формуле 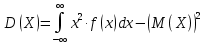 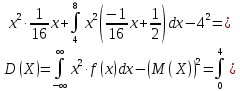 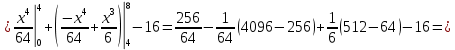 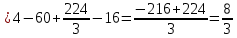 3. Среднее квадратическое отклонение равно 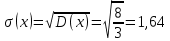 4. Модой Mo непрерывной случайной величины называется ёе значение, при котором плотность распределения имеет максимум. 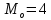 5. Медианой Me непрерывной случайной величины называется е значение, при котором имеет место равенство 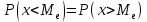 Из определения следует 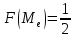 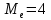 6. Коэффициентом асимметрии случайной величины называется величина 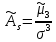 7. 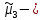 центральный момент 3-го порядка. центральный момент 3-го порядка.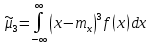 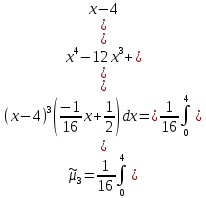 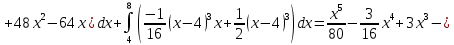 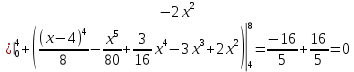 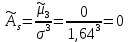 8. Эксцессом случайной величины называется величина 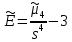 9. 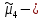 центральный момент 4-го порядка. центральный момент 4-го порядка.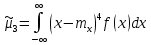 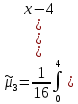 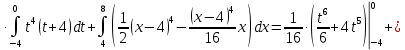 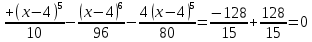 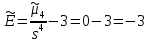 2) Вычислиь вероятности безусловных 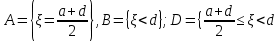 случайных событий и условного случайных событий и условного 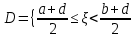 случайного события. случайного события.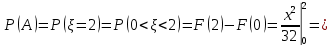 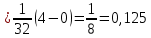 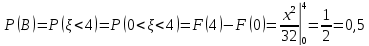 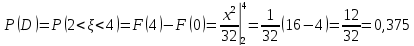 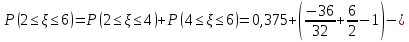 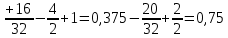 Задача 2. Дана двухмерная дискретная случайная величина 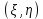 таблицей распределения в виде вероятностной матрицы. таблицей распределения в виде вероятностной матрицы. 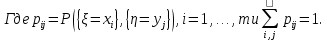 Требуется: 1) Определить частные законы распределения и основные (математическое ожидание, дисперсию и среднеквадратическое отклонение) числовые характеристики случайных величин и , совместную функцию распределения дискретной случайной величины (,) и вектора её характеристик центра распределения и рассеивания. 2) Найти условные законы распределения случайной величины от значений реализаций СВ, значения условного математического ожиданий, условной дисперсии, условного среднеквадратичного отклонения. 3) Построить графическое изображение совместного закона распределения двухмерной СВ в виде диаграммы рассеивания и наложенными на неё линями условного математического ожиданий и условного среднеквадратичного отклонения СВ | {=xi}. 4) Определить ковариацию, корреляцию, генеральное корреляционное отношение, функцию линейной регрессии и построить её график, совмещенный с графиками условного математического ожиданий и условного среднеквадратичного отклонения СВ | {=xi}. Исходные данные для задачи №2: 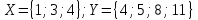
|
