задачи для экзамена 1 курс. задачи для экзамена. Тема Комплексные числа
 Скачать 142.23 Kb. Скачать 142.23 Kb.
|
|
Тема 1. Комплексные числа 1.1. Вычислить 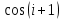 Записать действительную и мнимую части комплексного числа. 1.2. Найти x и yR: 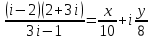 1.3.Извлечь корень из комплексного числа 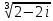 1.4. Вычислить, ответ записать в тригонометрической, алгебраической и показательной формах: 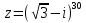 1.5. Изобразить область на комплексной плоскости, задаваемую неравенством: 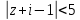 1.6. Вычислить, ответ записать в тригонометрической, алгебраической и показательной формах: 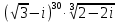 Тема 2. Многочлены 2.1. Выполнить деление с остатком 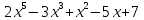 на на 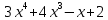 2.2. Не осуществляя деления и не используя схему Горнера найти остаток от деления полинома 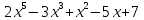 на на 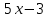 2.3. Определить кратность корня 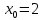 полинома полинома 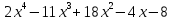 . .Разложить полином на множители. 2.4. Разложить полином 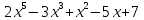 по степеням по степеням 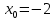 , используя схему Горнера. , используя схему Горнера.2.5. Построить полином наименьшей степени с действительными коэффициентами, если его корни: 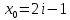 кратности 1, кратности 1, 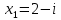 кратности 1 и кратности 1 и 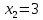 кратности 2. кратности 2.2.6. Найти НОД двух полиномов 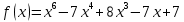 и и 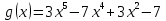 2.7. Пользуясь алгоритмом Евклида, подобрать полиномы M1(x) и M2(x) так, чтобы f(x)M1(x) + g(x)M2(x) = (x), где (x) – НОД полиномов f(x) и g(x), 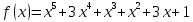 и и 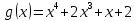 . .2.8. Пользуясь алгоритмом Евклида, подобрать полиномы M1(x) и M2(x) так, чтобы f(x)M1(x) + g(x)M2(x) = 1, где 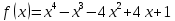 и и 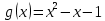 . .Тема 3. Матрицы и определители 3.1. Вычислить определитель a) 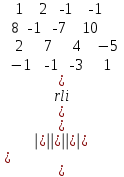 , ,b) 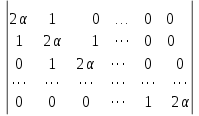 c) 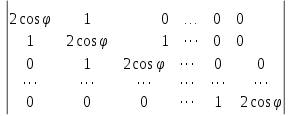 3.2. Вычислить ранг матрицы 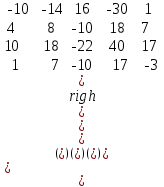 методом окаймления миноров. методом окаймления миноров.3.3. Найти обратную матрицу к матрице A: a) 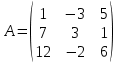 b) 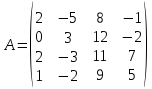 3.4.* Вычислить A2, если 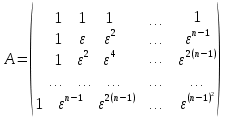 , при , при 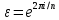 3.5. Вычислить a) 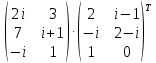 b) 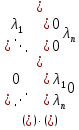 Тема 4. Системы линейных уравнений 4.1. Решить с помощью формул Крамера систему уравнений: 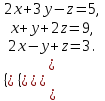 4.2. Найти фундаментальную систему решений для СЛОУ 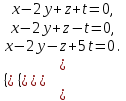 4.3. Выяснить, образуют ли строки каждой из матриц 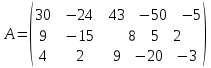 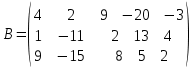 фундаментальную систему решений для системы уравнений: 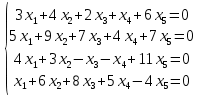 4.4. Исследовать систему уравнений на совместность, используя метод исключения неизвестных 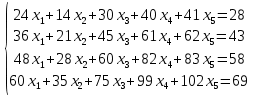 На оценку «3» будет система с меньшим количеством переменных. Тема 5. Векторная алгебра 5.1. Вычислить проекцию вектора 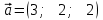 на ось вектора на ось вектора 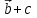 , если , если 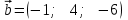 и и 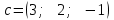 . .5.2. Векторы 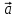 и и 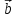 образуют угол 60°, причем образуют угол 60°, причем 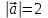 , , 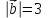 . Определить угол между векторами . Определить угол между векторами 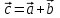 и и 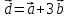 . .5.3. Вычислить синус угла, образованного векторами 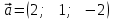 и и 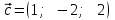 . .5.4. Зная векторы, образующие треугольник:  , , 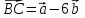 , , 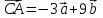 , где , где 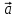 и и 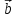 взаимно перпендикулярные орты, определить внутренние углы этого треугольника. взаимно перпендикулярные орты, определить внутренние углы этого треугольника.5.5. Средствами векторной алгебры вычислить длину высоты СН треугольника с вершинами в точках 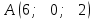 , , 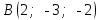 и и 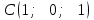 . .5.6. Векторы 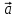 и и 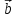 образуют угол 120°, причем образуют угол 120°, причем 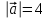 , , 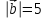 . Определить угол между векторами . Определить угол между векторами 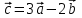 и и 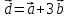 . .5.7. Будут ли компланарными векторы 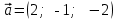 , , 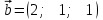 и и 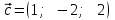 ? ?5.8. Найти разложение вектора 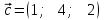 по базису состоящему из векторов по базису состоящему из векторов 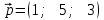 , , 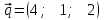 , , 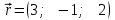 . .5.9. Векторы 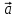 и и 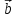 взаимно перпендикулярны. Зная, что взаимно перпендикулярны. Зная, что 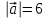 , , 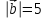 , вычислить , вычислить 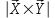 при условии, что при условии, что 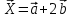 , , 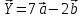 . .5.10. Средствами векторной алгебры вычислить площадь треугольника АВС, если 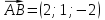 , , 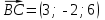 . .5.11. Даны координаты точек 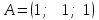 , , 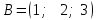 , , 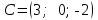 , D(2, 1,0). Вычислить , D(2, 1,0). Вычислить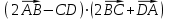 , , 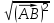 , , 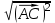 . .5.13. Определить, будет ли параллелограмм, построенных на приведенных к общему началу векторах 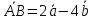 и и 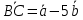 как на сторонах, прямоугольником или ромбом, если как на сторонах, прямоугольником или ромбом, если 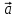 и и 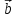 взаимно перпендикулярные орты. взаимно перпендикулярные орты.Тема 6. Прямая на плоскости 6.1. Зная две соседние вершины А (-6; 1) и В (-9; 12) параллелограмма ABCD и точку О (0; 7) пересечения диагоналей, найти его площадь. 6.2. Зная две соседние вершины А (6; 1) и В (9; 16) параллелограмма ABCD и точку О(10; 7) пересечения диагоналей, составить уравнения его сторон. 6.3. В треугольнике, вершинами которого являются точки К (2; -6), М(6; -1) и Р(4;0), найти длину перпендикуляра, опущенного из вершины К на медиану МН. 6.4. Составить уравнение прямой, параллельной прямым x-3y+10=0 и x-3y+15=0 и проходящей посередине между ними. 6.5. Составить уравнения высот треугольника АВС, если известны уравнения его сторон 5x-4y-1=0, x+10y-11=0 и 3х-у-7=0. 6.6. Составить уравнение прямой, параллельной прямой 5x-12y+18 =0, расстояние которой до точки М (1;7) равно 9. 6.7. Составить уравнение прямой, параллельной прямой 8x-6y+7=0, отклонение от которой точки М(0;0) равно -7. 6.8. В треугольнике, вершинами которого являются точки К(1; 4), М(-2; 0) и Р(1;2), найти угол между стороной МР и медианой, проведенной из вершины К. 6.9. Составить уравнения сторон треугольника АВС, если даны одна из его вершин В (3; -7) и уравнения двух высот 8x+3y+1=0 и 5x+y-17=0. 6.10. Составить уравнения сторон треугольника АВС, если даны одна из его вершин С (-9; -3) и уравнения высоты 9x-8y-1=0 и медианы 5x+4y-9=0, проведенных из одной вершины. 6.11. Зная вершины А (-6; -1), В (-9; 16) и С (10; 7) треугольника, составить уравнение высоты, проведенной из вершины В. 6.12. Зная вершины А (-6; 0), В(0; 16) и С(10; -3) треугольника, составить уравнение биссектрисы, проведенной из вершины А. 6.13. Зная вершины А (-6; 1), В (-9; 16) и С (10; -7) треугольника, составить уравнение медианы, проведенной из вершины С. Тема 7. Прямая и плоскость в пространстве. 7.1. Составить уравнение плоскости, перпендикулярной вектору 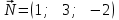 и отсекающей на оси Ох отрезок и отсекающей на оси Ох отрезок 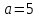 . .7.2. Составить уравнения плоскостей, которые делят пополам двугранный угол, образованный плоскостями 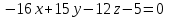 и и 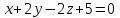 . .7.3. Составить уравнение плоскости, проходящей через точки 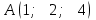 и и 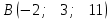 параллельно оси параллельно оси 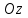 . .7.4. Две грани куба лежат на плоскостях 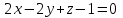 и и 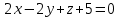 . Вычислить объем этого куба. . Вычислить объем этого куба.7.5. Составить канонические уравнения прямой 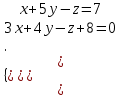 7.6. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 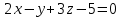 и и 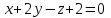 параллельно вектору параллельно вектору 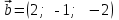 . .7.7. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 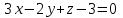 и и 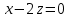 и перпендикулярно плоскости и перпендикулярно плоскости 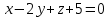 . .7.8. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 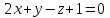 и и 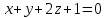 параллельно отрезку, ограниченному точками параллельно отрезку, ограниченному точками 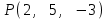 и и 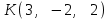 . . 7.9. Составить уравнение плоскости, параллельной вектору 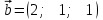 и отсекающей на осях Ох и Оу отрезки 3 и -7 соответственно. и отсекающей на осях Ох и Оу отрезки 3 и -7 соответственно.7.10. Даны вершины треугольника А(3; -1; -1), В(1; 2; -7) и С(-5; 14; -3). Составить параметрические уравнения биссектрисы его внутреннего угла при вершине В. 7.11. Составить уравнение плоскости, отклонение точек которой от плоскости 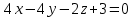 равно -3. равно -3.7.12. Пересекает ли плоскость 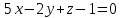 отрезок, ограниченный точками отрезок, ограниченный точками 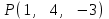 и и 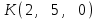 . Ответ обосновать. . Ответ обосновать.7.13. Найти расстояние между прямыми 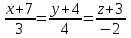 и и 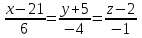 . .7.14. На оси Оу найти точку, равноудаленную от точки 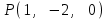 и плоскости и плоскости 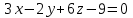 . .7.15. Вычислить расстояние от точки 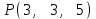 до прямой до прямой 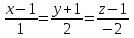 . .7.16. Вычислить углы, образуемые нормалью к плоскости 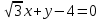 , и расстояние , и расстояние 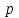 от начала координат до плоскости. от начала координат до плоскости.7.17. Вычислить объем пирамиды, ограниченной плоскостью 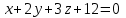 и координатными плоскостями. и координатными плоскостями.7.18. Вычислить радиус сферы, которая касается плоскостей 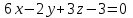 и и 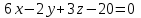 . .7.19. Определить, лежат ли точка 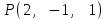 и начало координат по одну или по разные стороны относительно плоскости и начало координат по одну или по разные стороны относительно плоскости 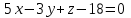 . .7.20. Даны вершины треугольника А(3; 6; -7), В(-5; 2; 3) и С(4; -7; -2). Составить параметрические уравнения его медианы, проведенной из вершины С. |
