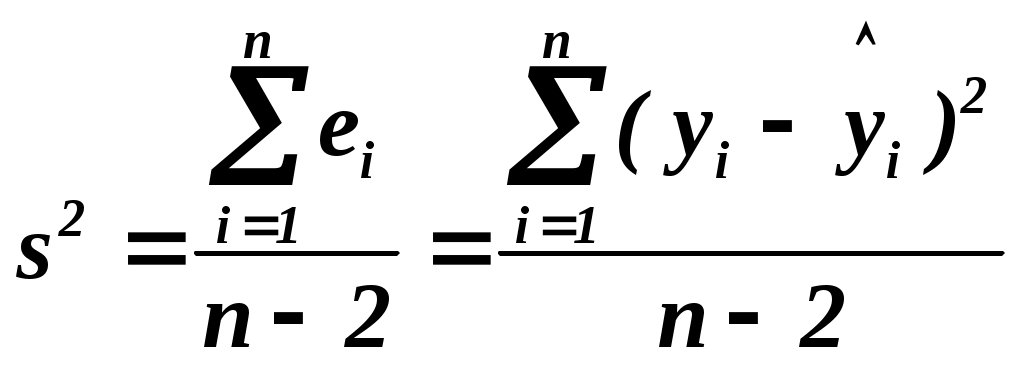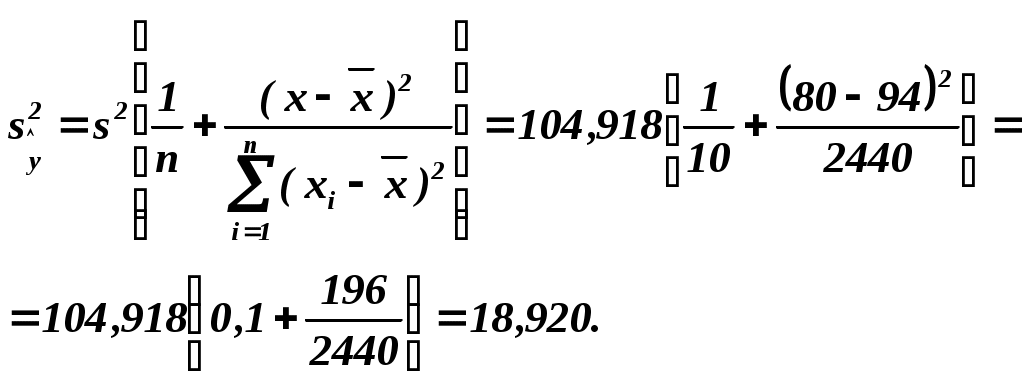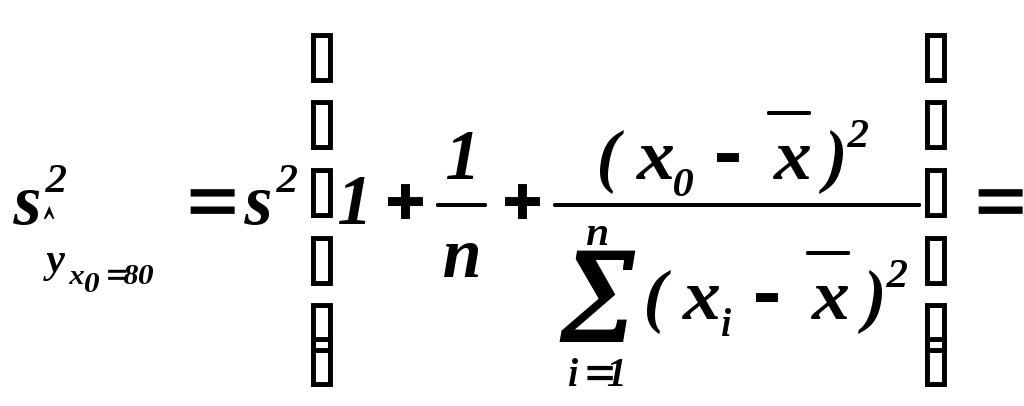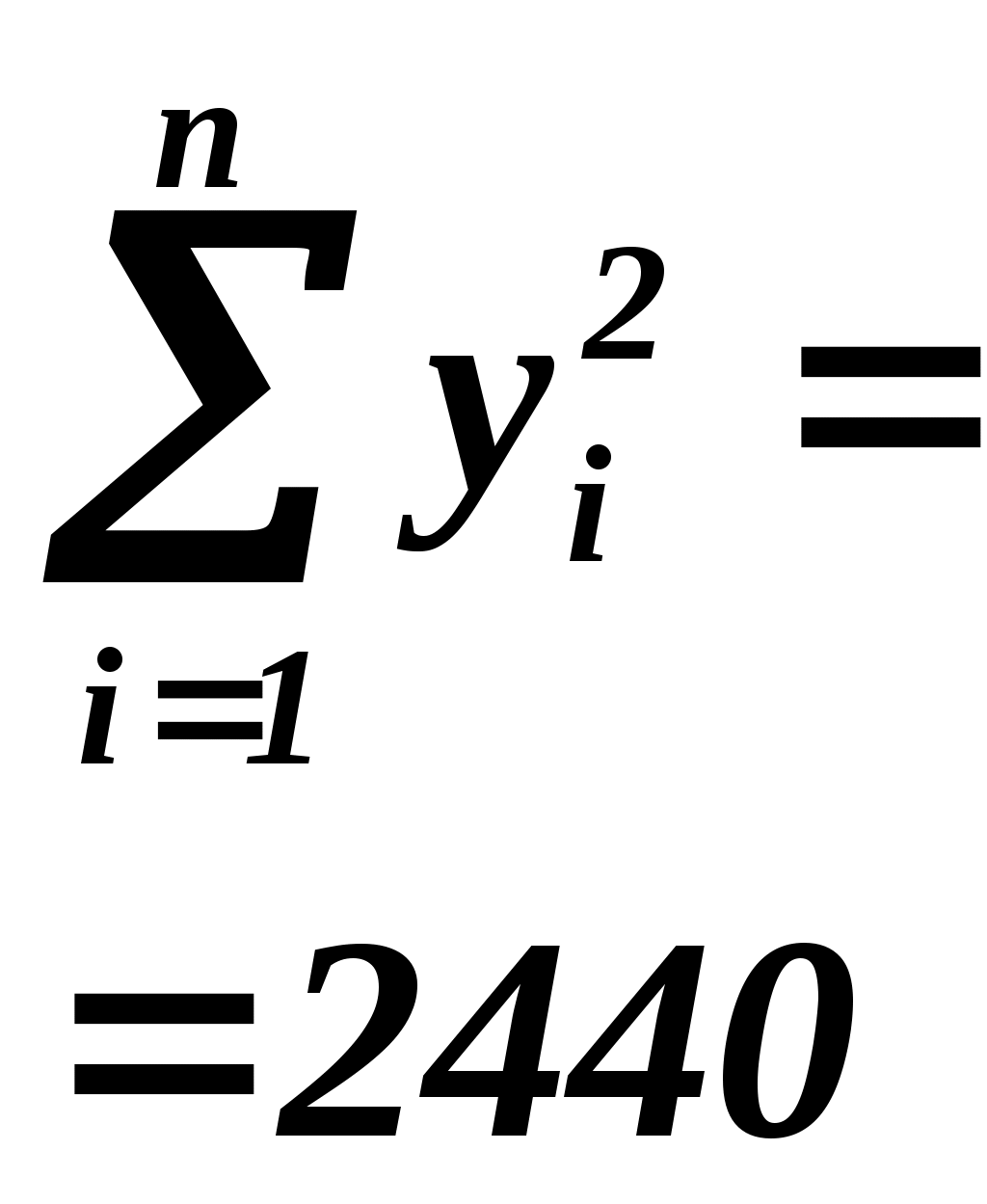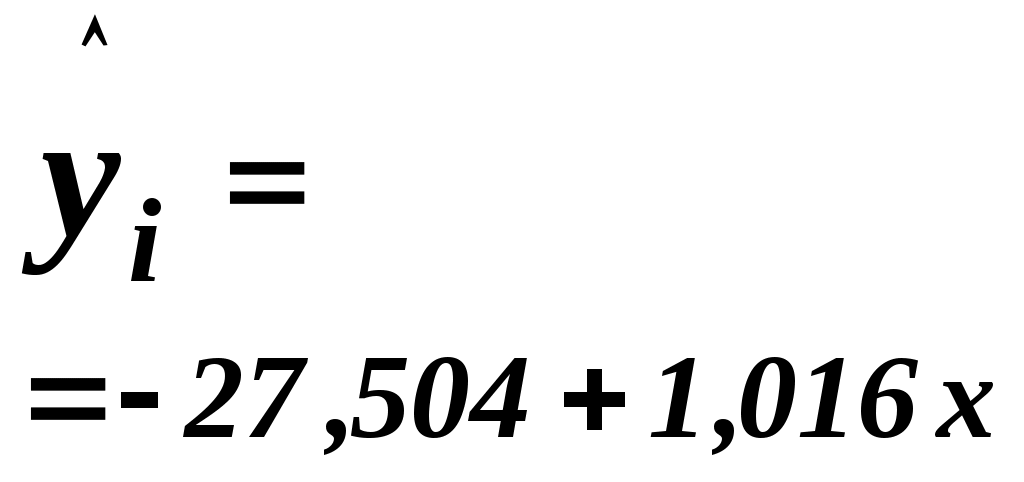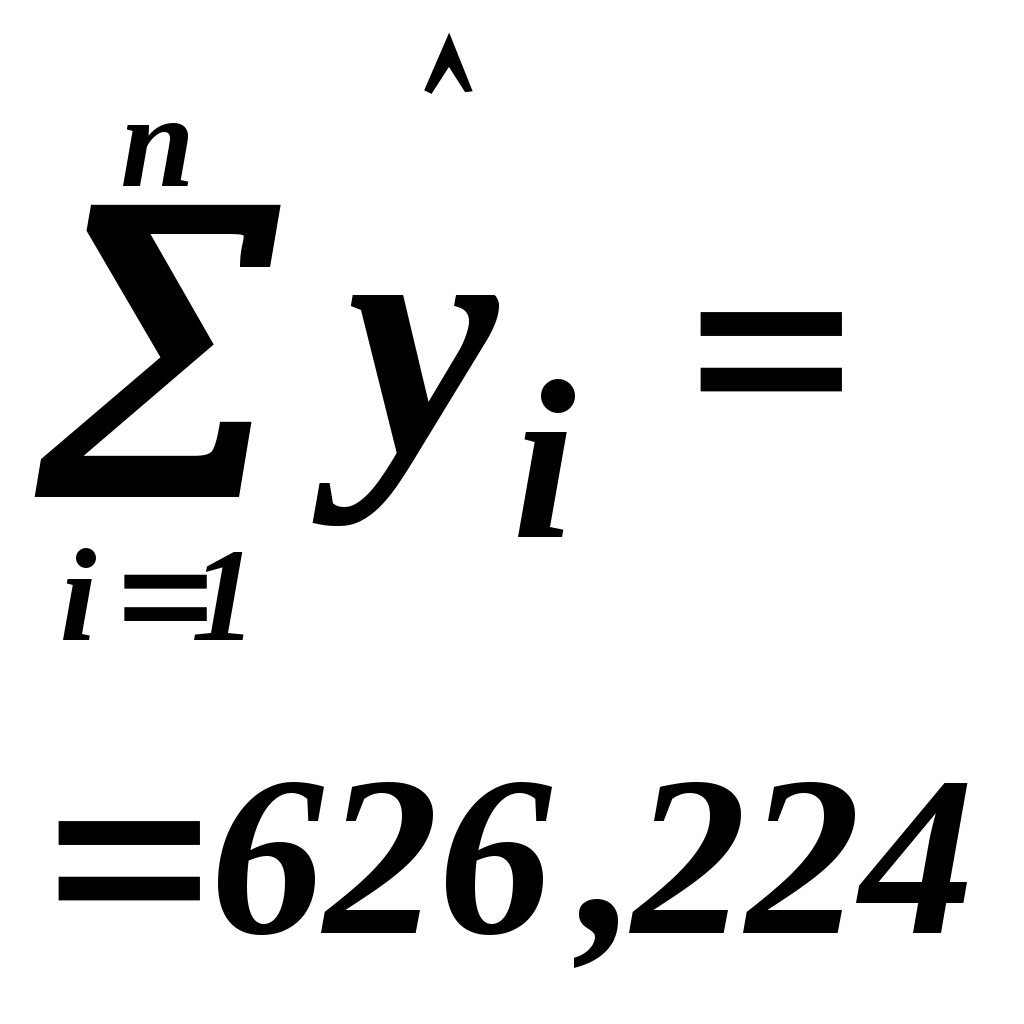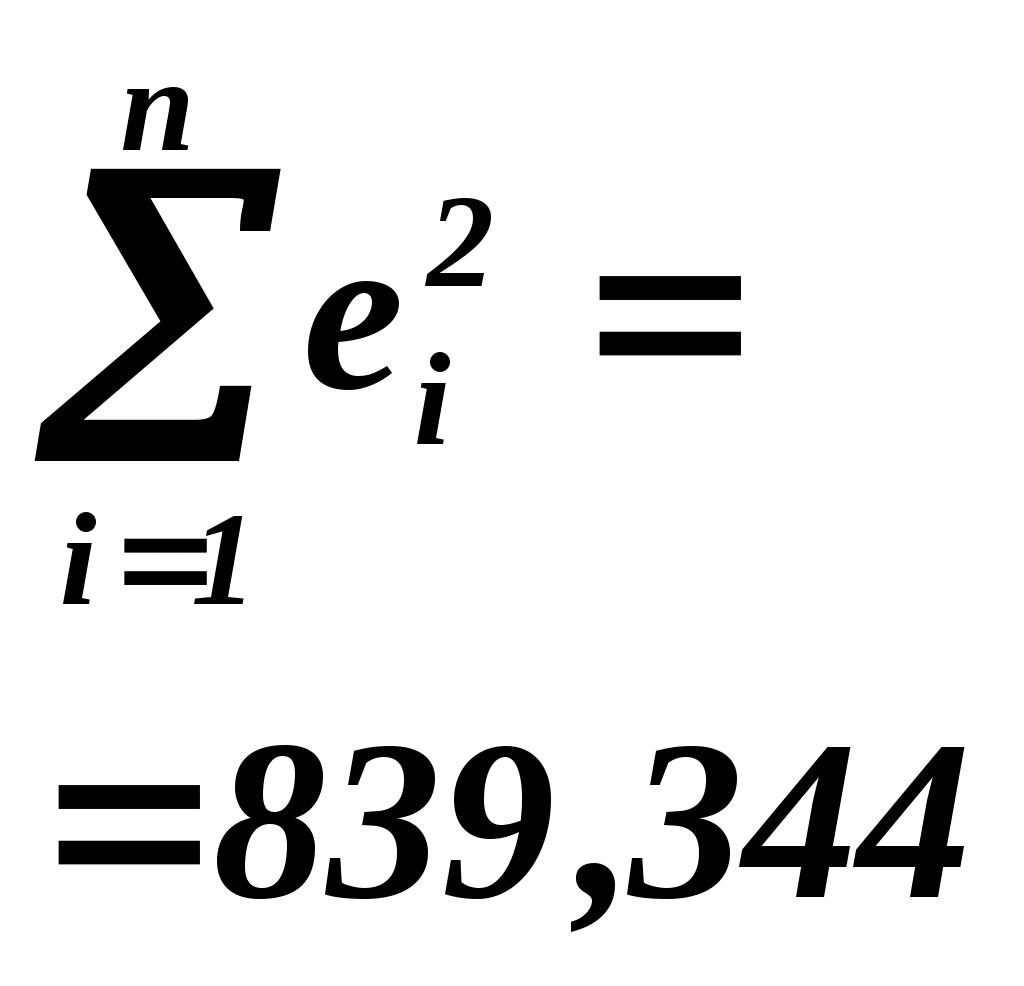б). Уравнение регрессии в отклонениях. Чтобы записать уравнение регрессии в отклонениях построим таблицу 1.2:
Таблица 1.2

|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
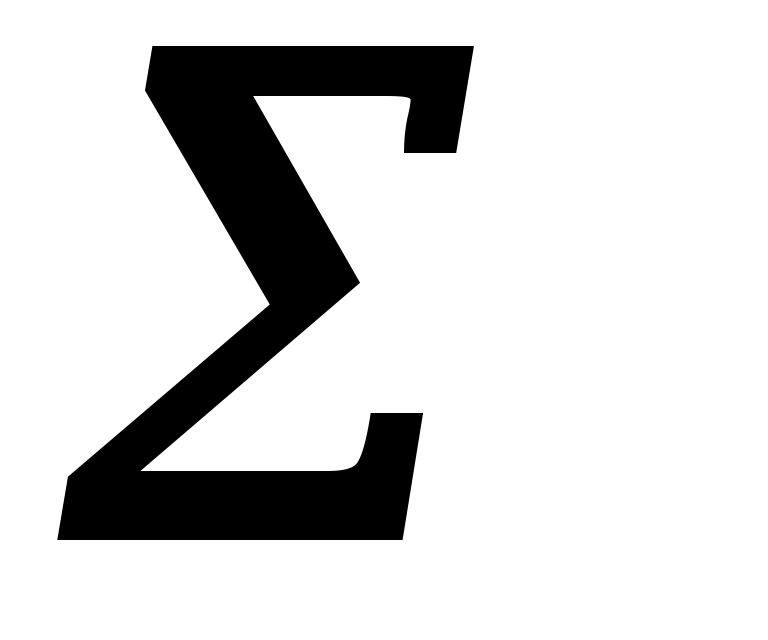
|
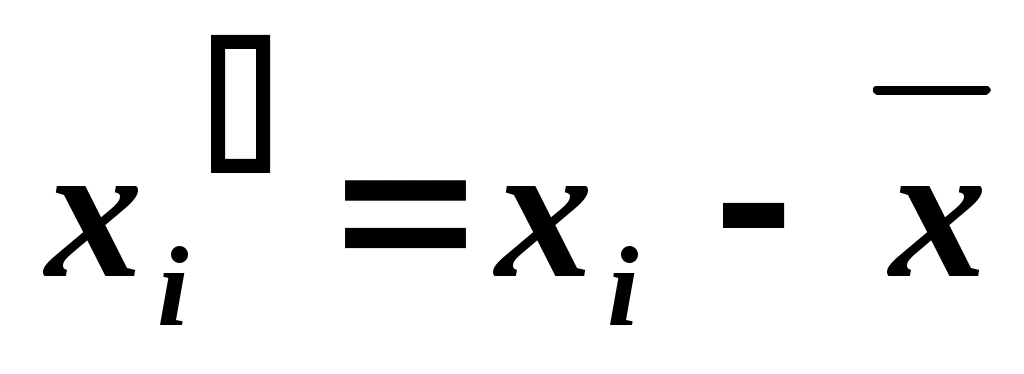
|
-14
|
16
|
26
|
-4
|
-14
|
-14
|
-4
|
-4
|
-14
|
26
|
|
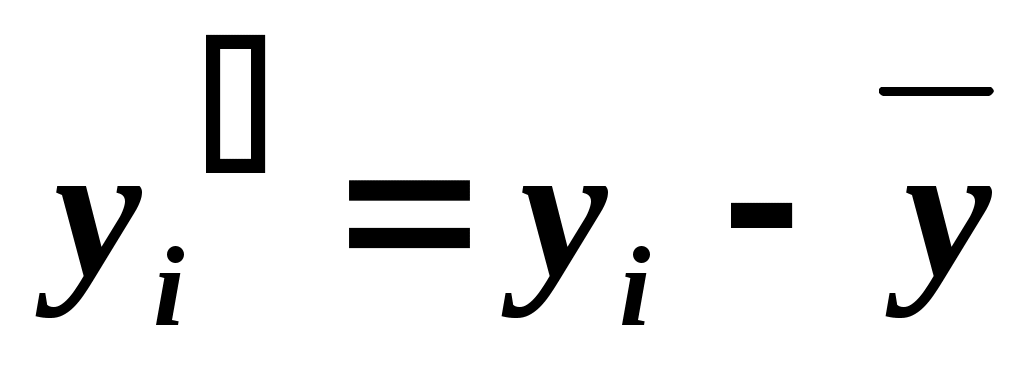
|
-18
|
32
|
32
|
2
|
-18
|
-8
|
-8
|
-18
|
-8
|
12
|
|
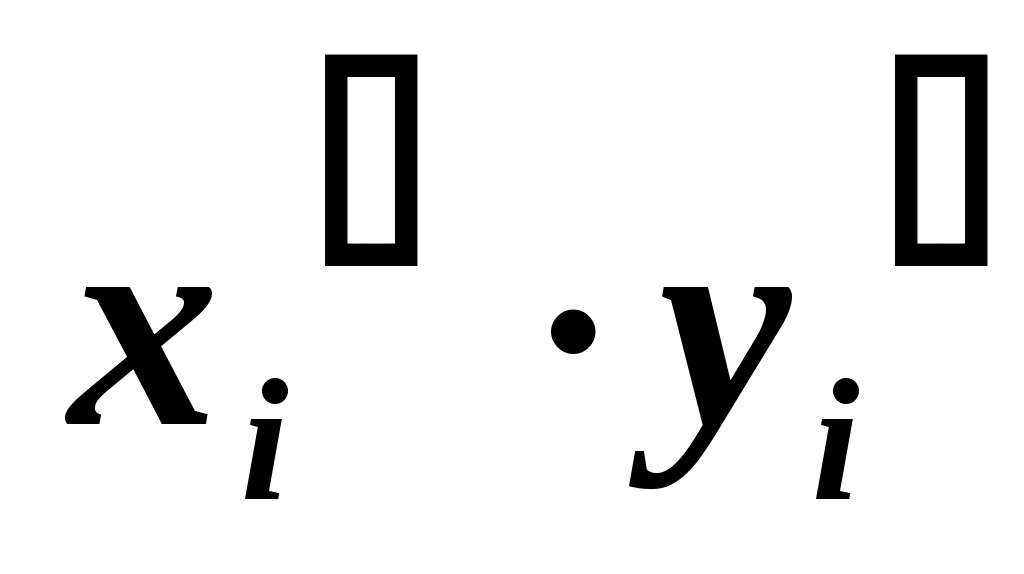
|
252
|
512
|
832
|
-8
|
252
|
112
|
32
|
72
|
112
|
312
|
2480
|
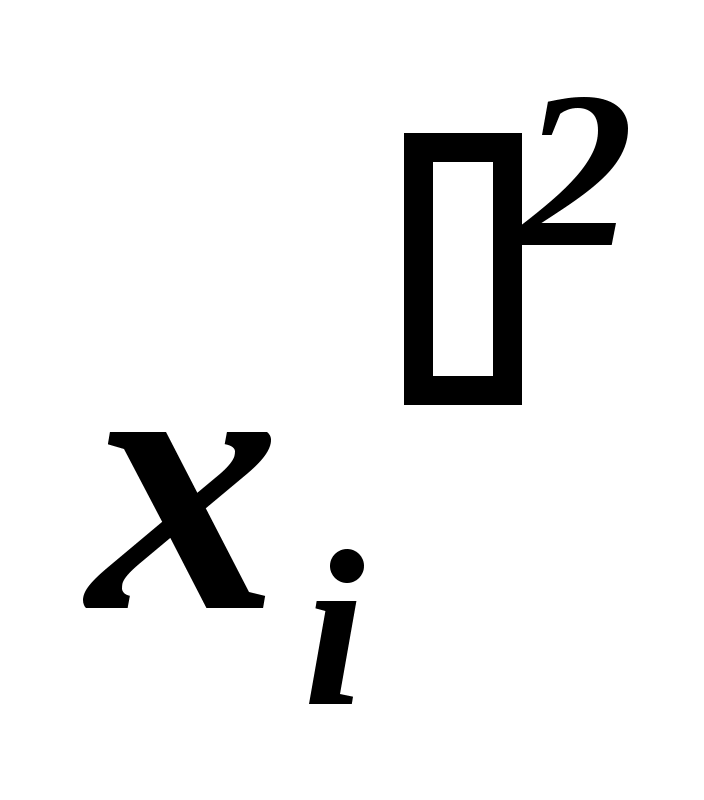
|
196
|
256
|
676
|
16
|
196
|
196
|
16
|
16
|
196
|
676
|
2440
|
Следовательно,  . .
Уравнение регрессии в отклонениях будет иметь вид:  . .
в). Уравнение регрессии в матричной форме. Из условия задачи:
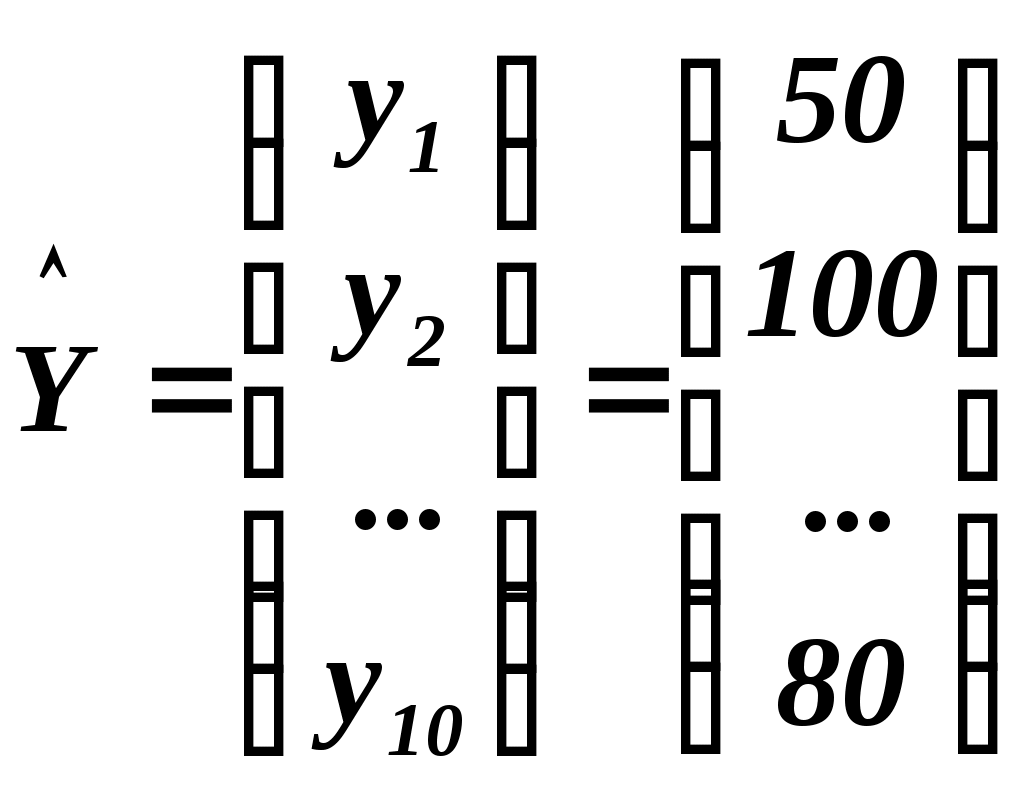 , , 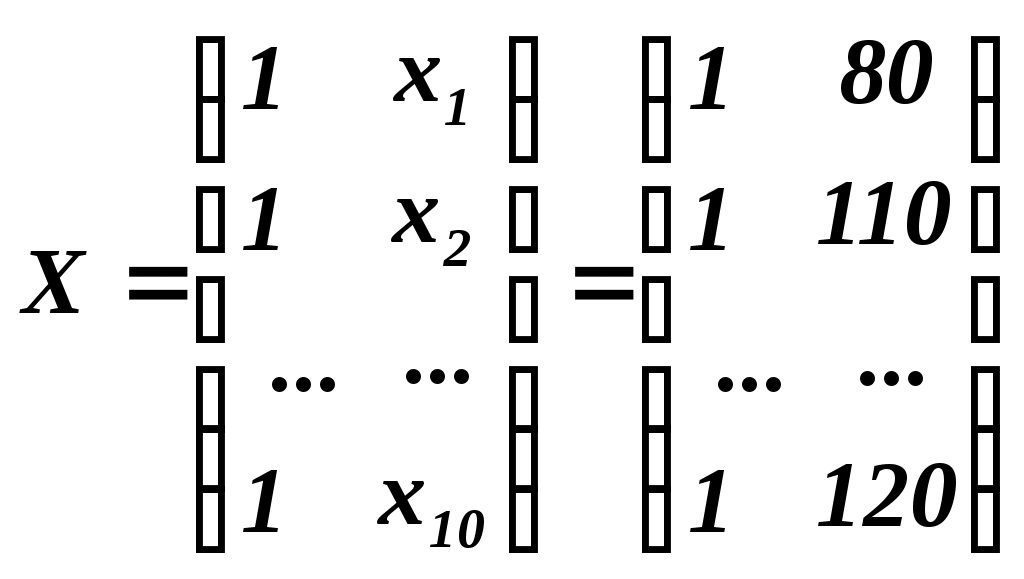 . .
Тогда  . .
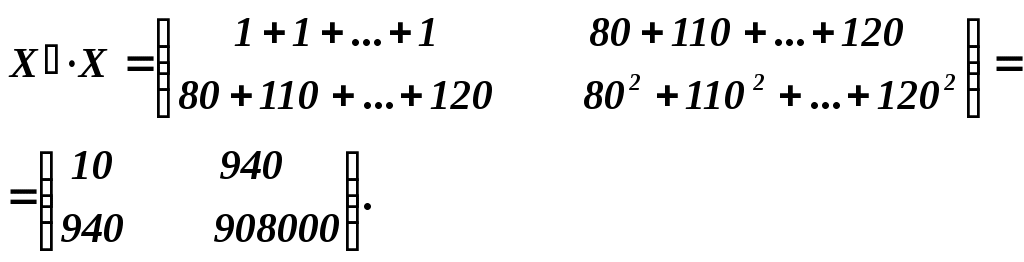
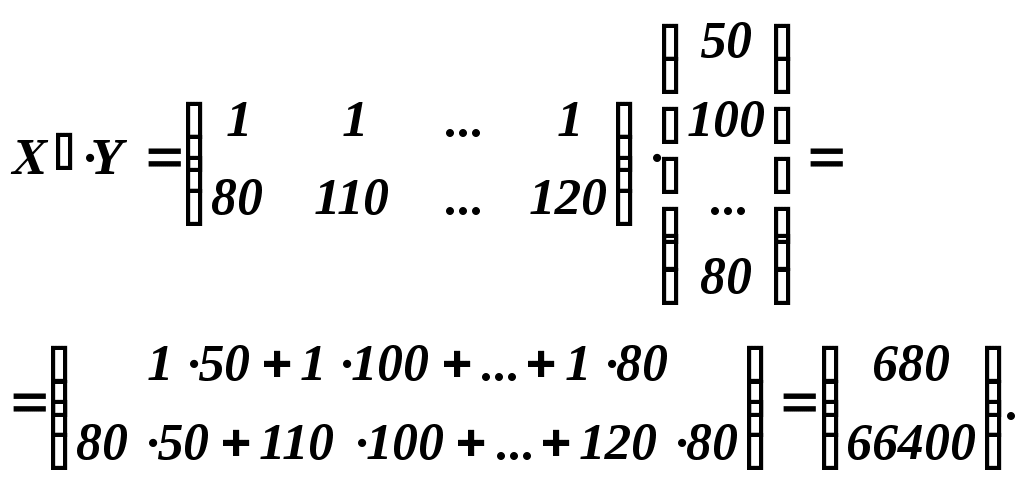
Найдем  , т.е. обратную матрицу для матрицы ( , т.е. обратную матрицу для матрицы ( ). ).
 , следовательно, обратная матрица существует. Найдем алгебраические дополнения для каждого элемента определителя (алгебраические дополнения вычисляются по формуле , следовательно, обратная матрица существует. Найдем алгебраические дополнения для каждого элемента определителя (алгебраические дополнения вычисляются по формуле 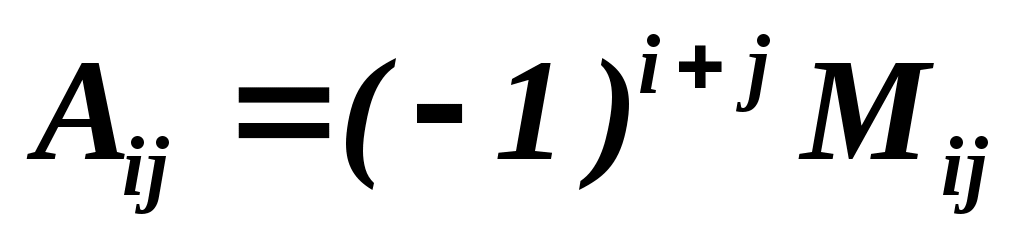 , обратная матрица для матрицы , обратная матрица для матрицы 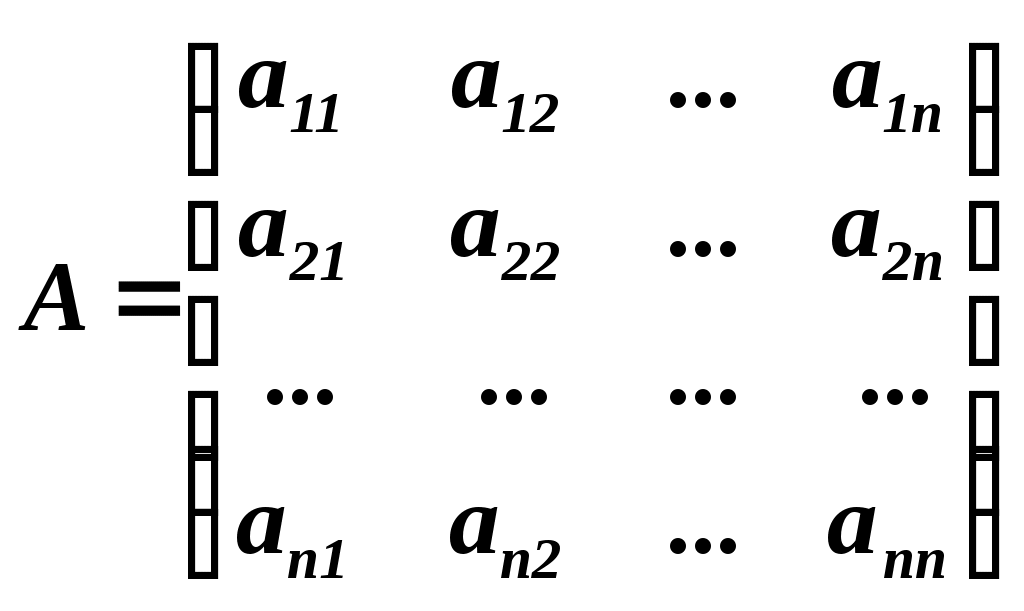 находится по формуле находится по формуле 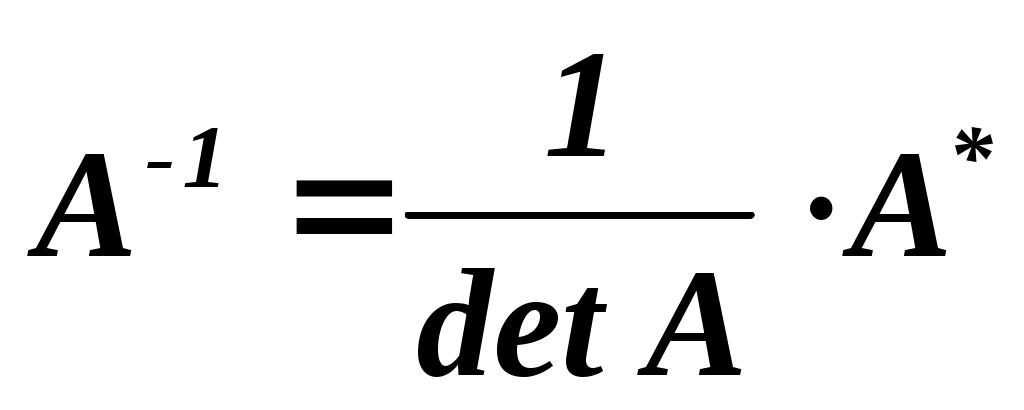 , где , где 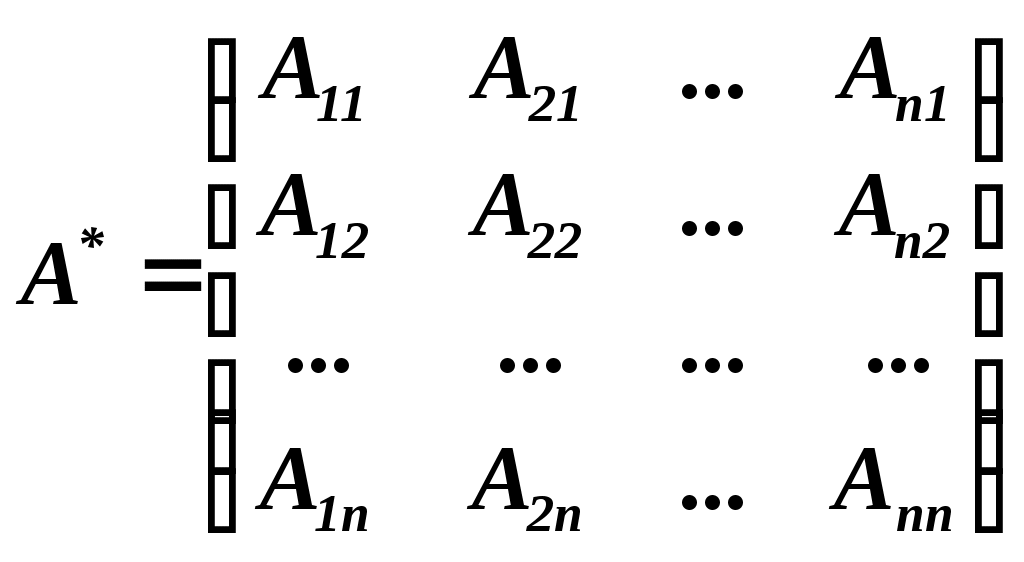 ). ).
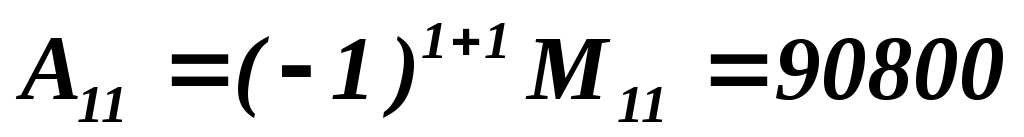 , ,  , ,
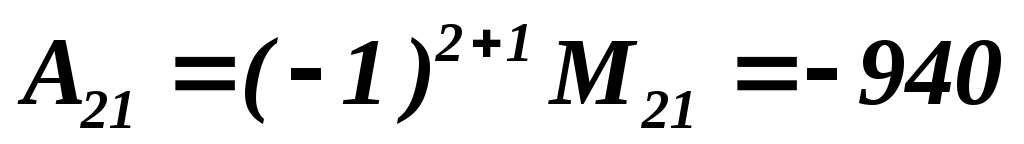 , , 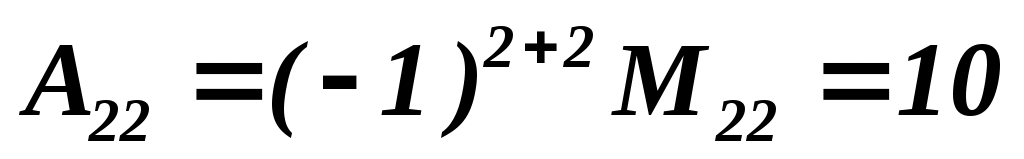 . .
Следовательно,  . .
Значит,
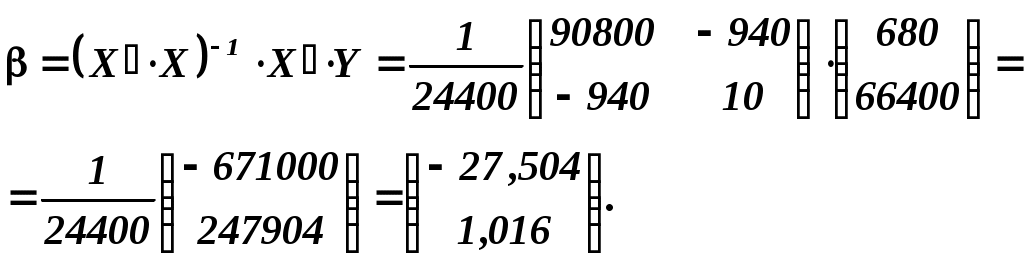
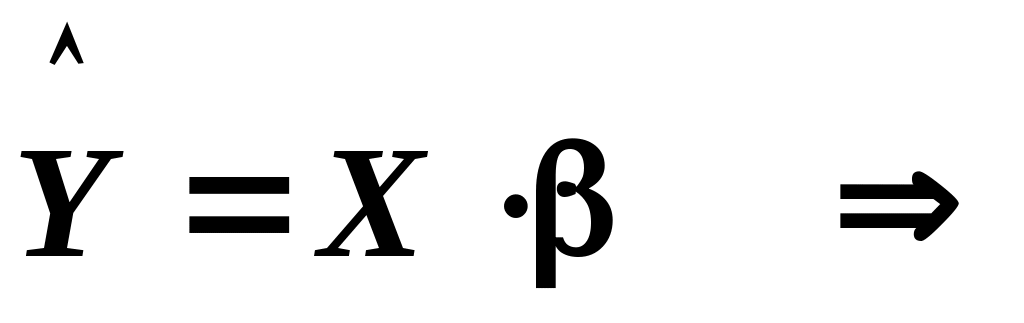 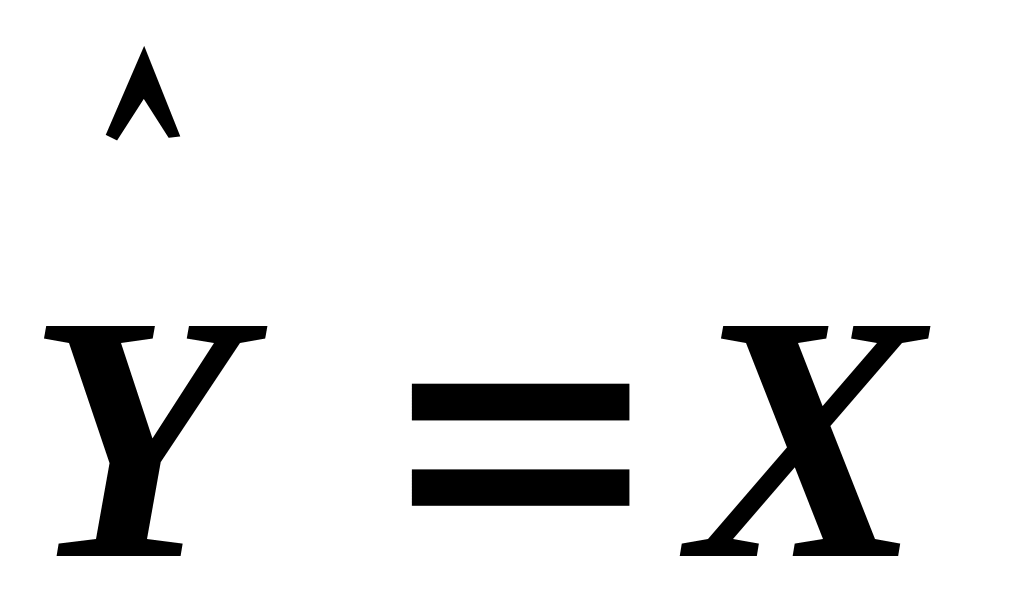 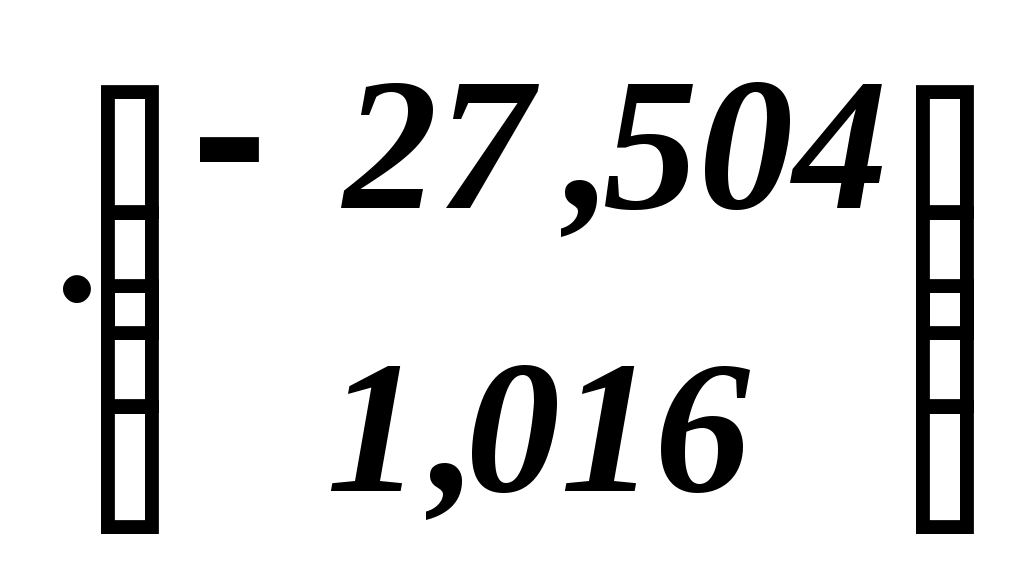 - уравнение регрессии в матричной форме. - уравнение регрессии в матричной форме.
Вычислить коэффициент корреляции между переменными Y и X.
Для его вычисления воспользуемся формулой:
 . .
Из задачи 1 известно, что 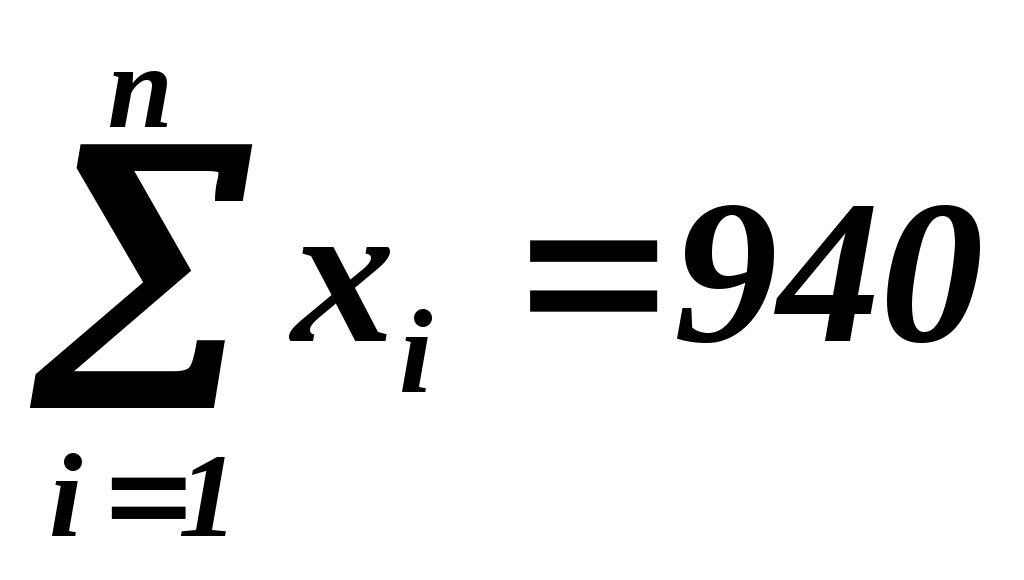 , ,  , , 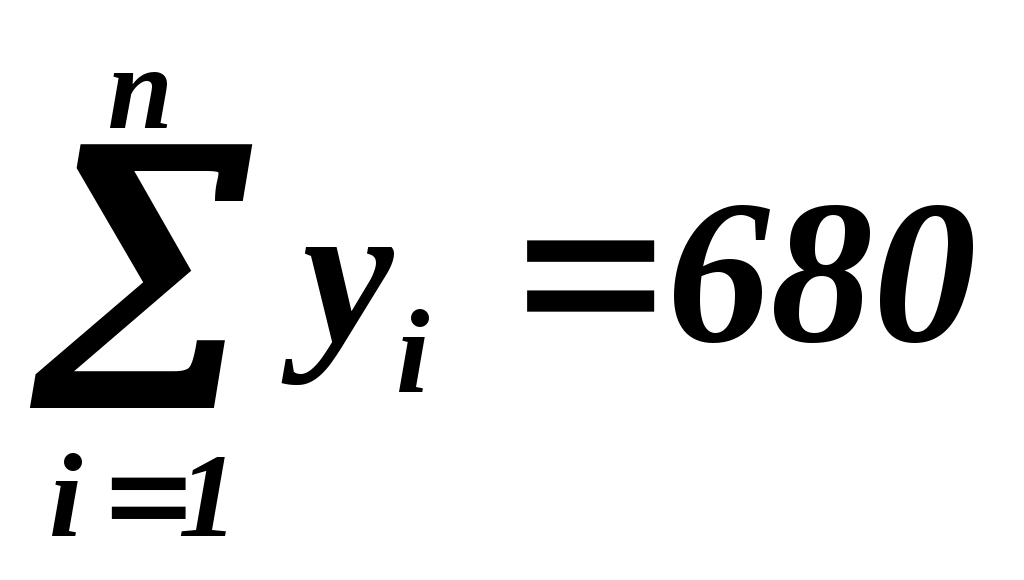 , , 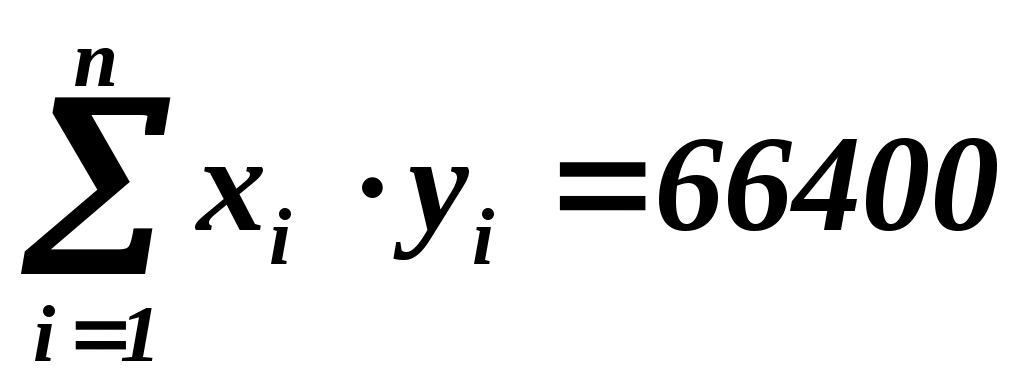 , а , а 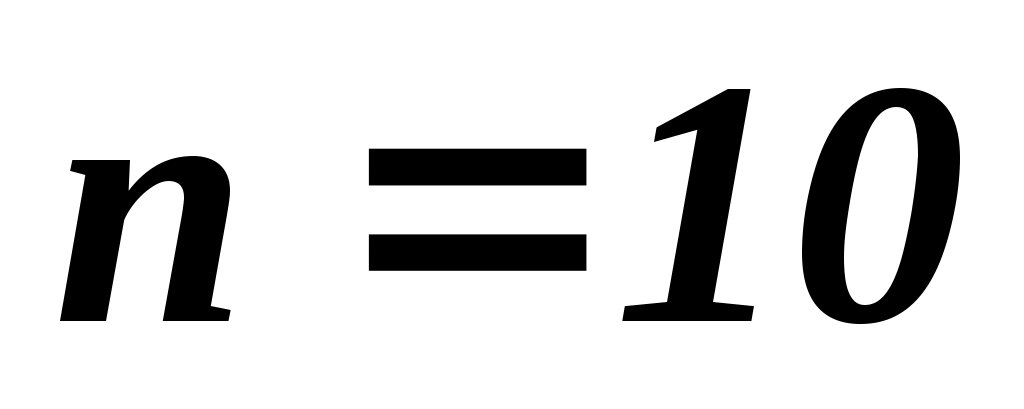 - из условия примера. Найдем - из условия примера. Найдем 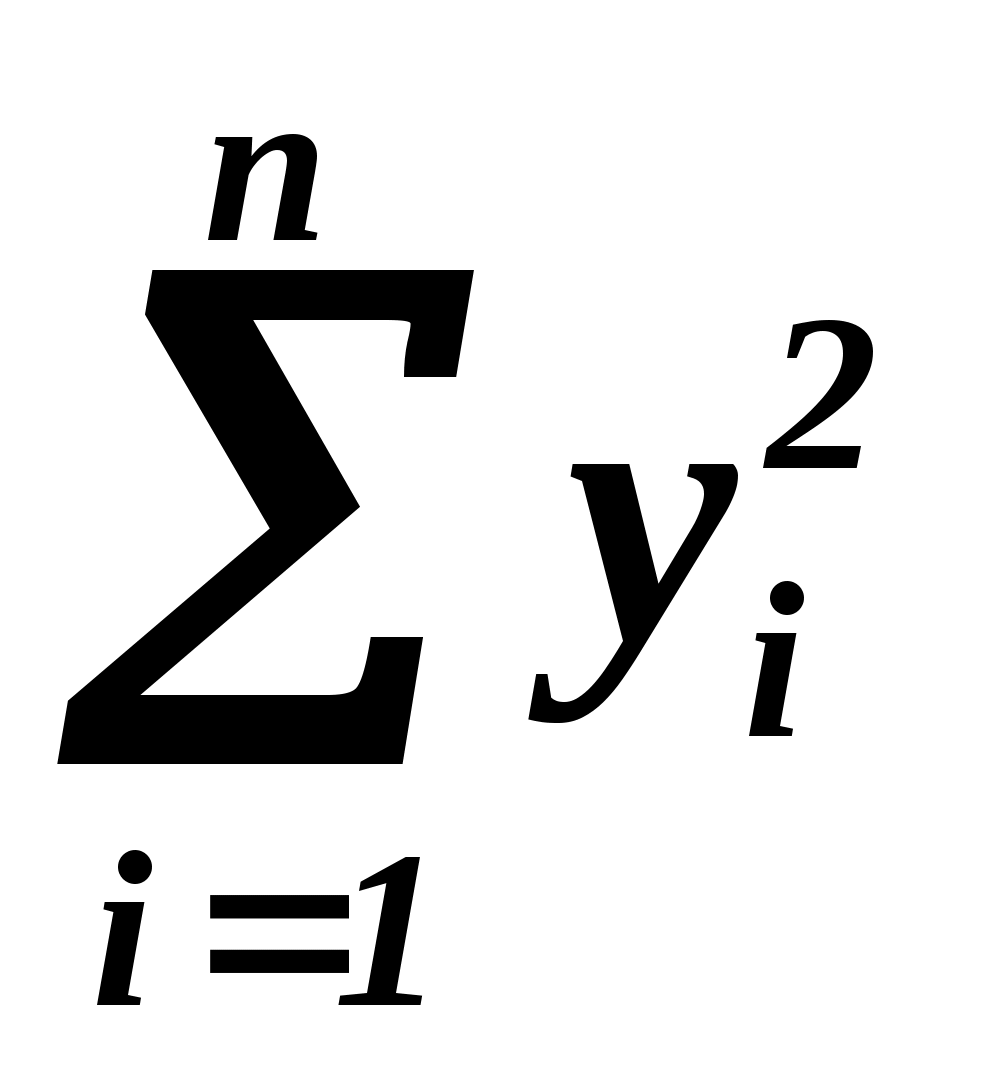 , т.е. дополним таблицу 1.2 еще одной строкой. , т.е. дополним таблицу 1.2 еще одной строкой.
Таблица 1.3
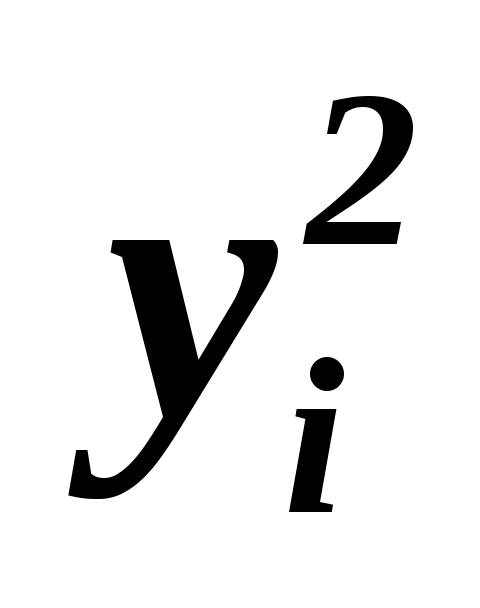
|
502=
2500
|
10000
|
10000
|
4900
|
2500
|
3600
|
3600
|
2500
|
3600
|
6400
|
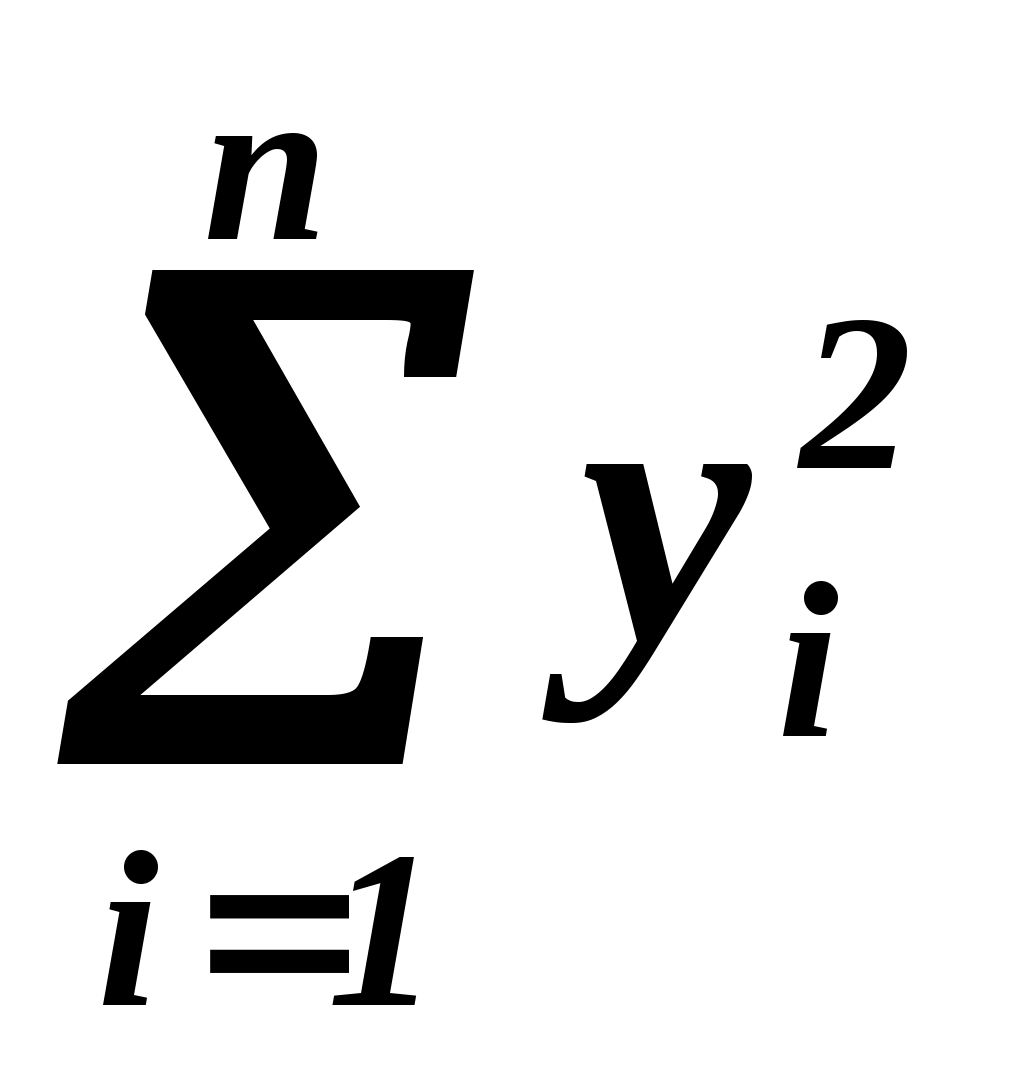 = =
49600
|
Тогда
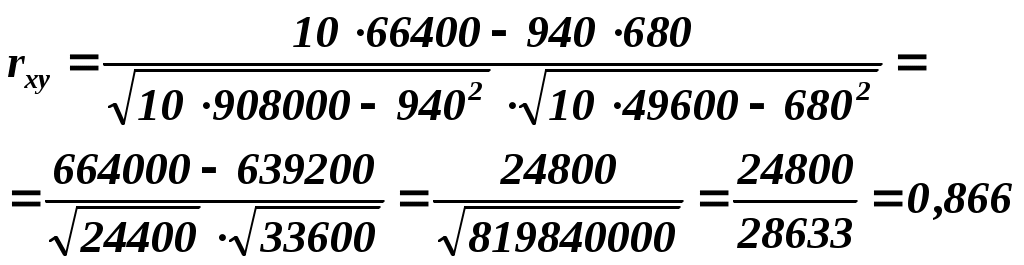 , ,
т.е. связь между переменными Y и Xдостаточно тесная.
Проверить значимость коэффициента корреляции между переменными Y и X.
Выдвинем гипотезу 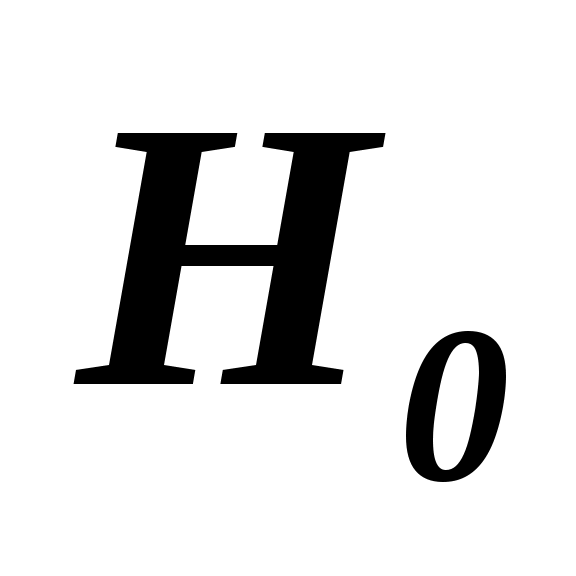 об отсутствии линейной корреляционной связи между переменными X и Y. об отсутствии линейной корреляционной связи между переменными X и Y.
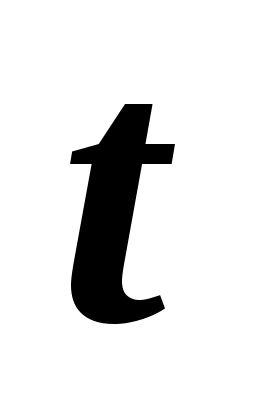 факт факт 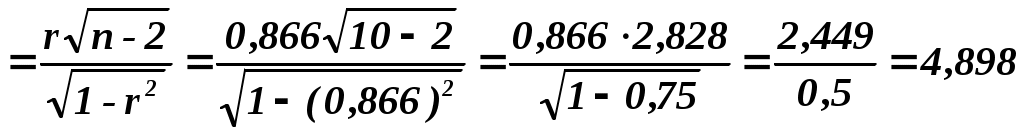 . .
Для уровня значимости  =0,05 и =0,05 и 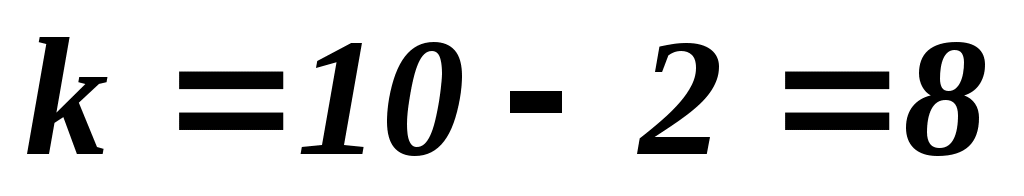 найдем табличное значение найдем табличное значение 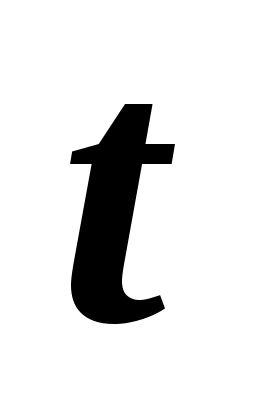 - критерия Стьюдента: - критерия Стьюдента:
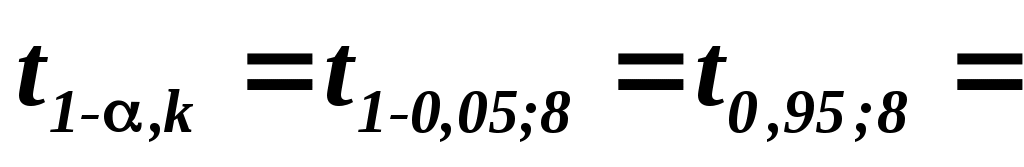  по таблице II приложений по таблице II приложений 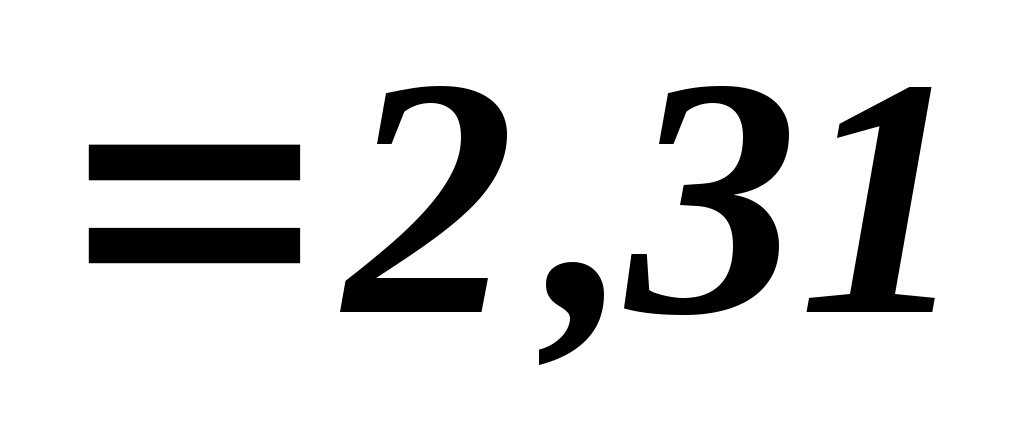 . .
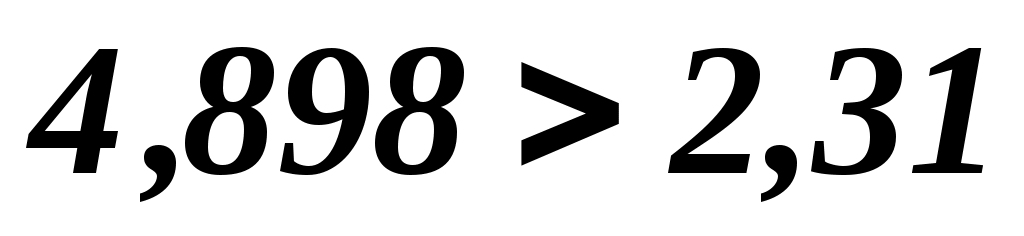 , т.е. , т.е. 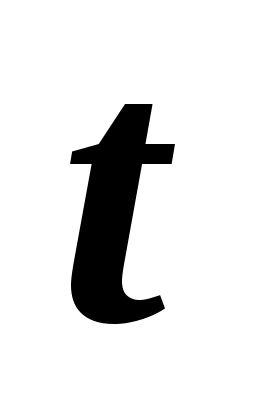 факт факт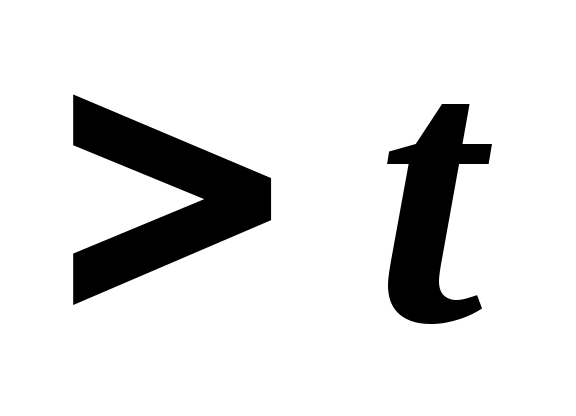 табл, следовательно, гипотеза табл, следовательно, гипотеза 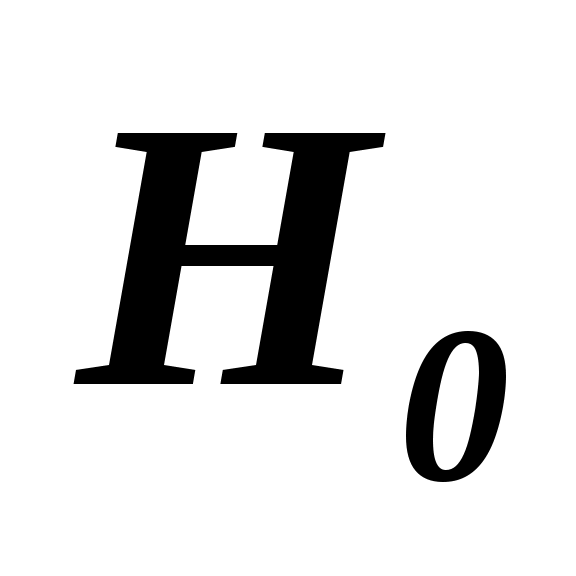 отвергается, а значит, коэффициент корреляции между значением оценки этих компаний Y и фактической стоимостью компании X значительно отличается от нуля, т.е. отвергается, а значит, коэффициент корреляции между значением оценки этих компаний Y и фактической стоимостью компании X значительно отличается от нуля, т.е. 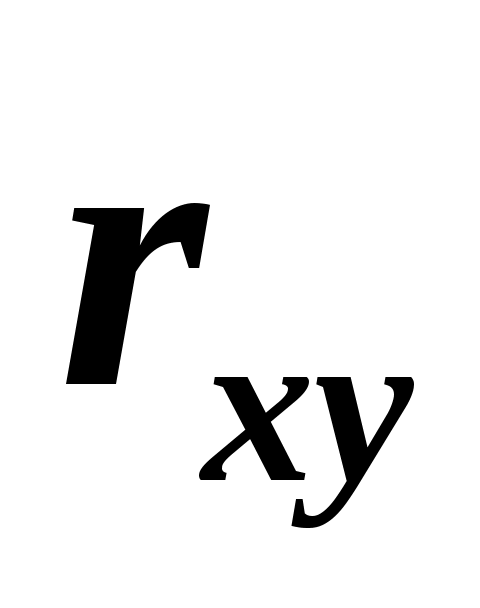 - значим. - значим.
Оценить среднее значение оценки компании с фактической стоимостью 80 усл. ден. ед., т.е. оценить условное математическое ожидание 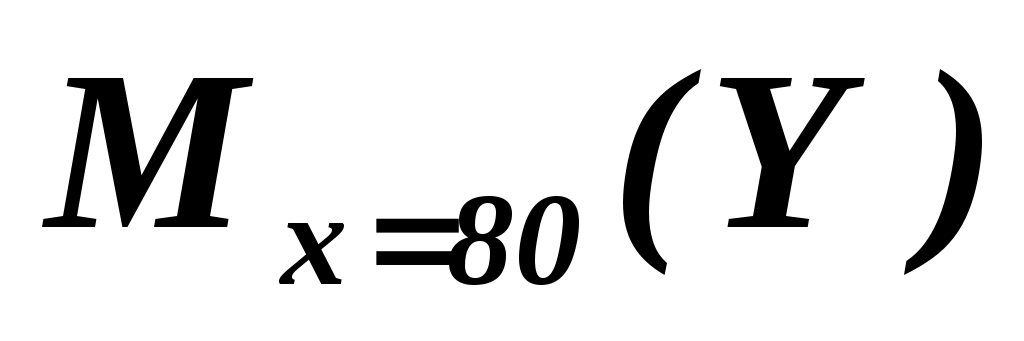 . .
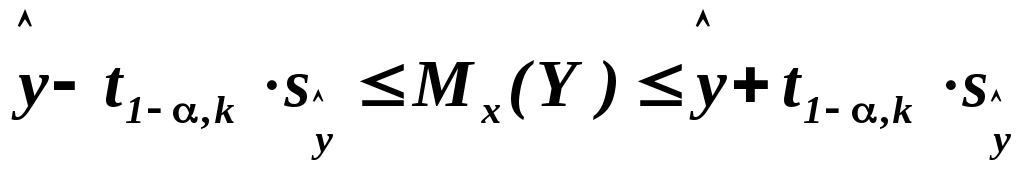 . .
Уравнение регрессии Y по Xимеет вид 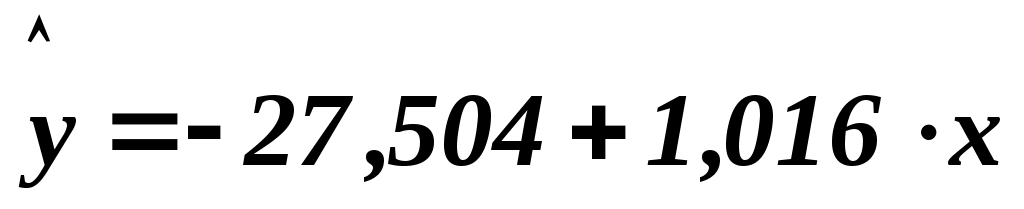 . .
Выборочной оценкой 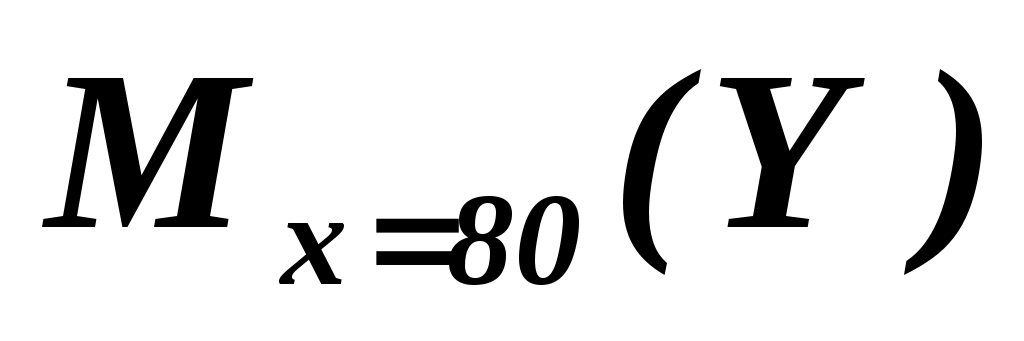 является групповая средняя является групповая средняя  , которую найдем по уравнению регрессии: , которую найдем по уравнению регрессии:  . .
Для построения доверительного интервала для 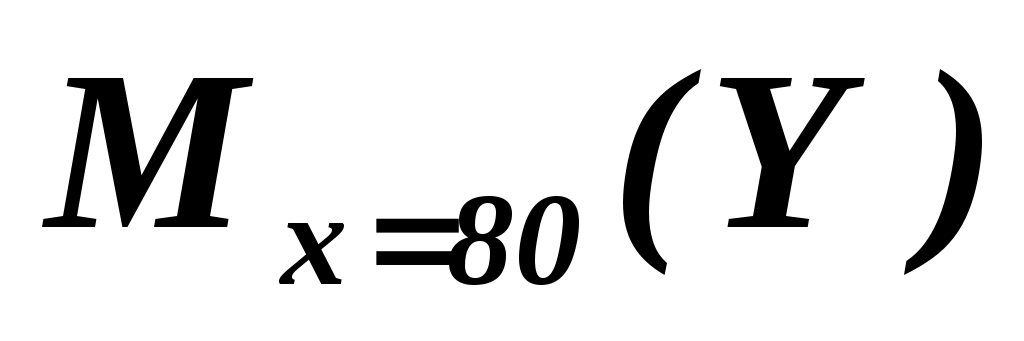 необходимо знать дисперсию его оценки, т.е. необходимо знать дисперсию его оценки, т.е. 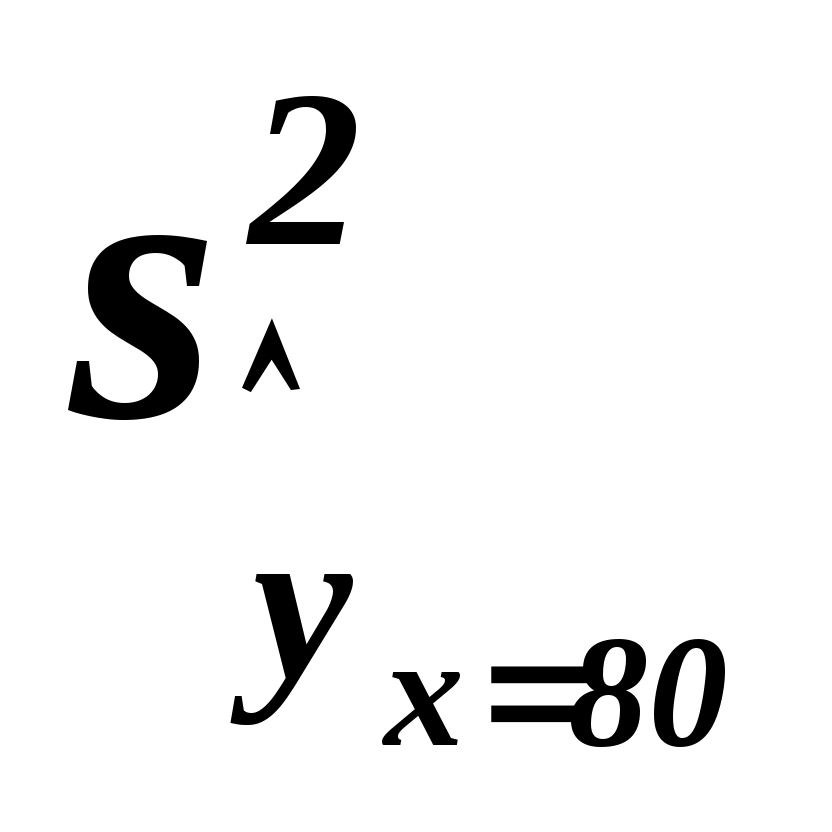 . Для вычисления . Для вычисления 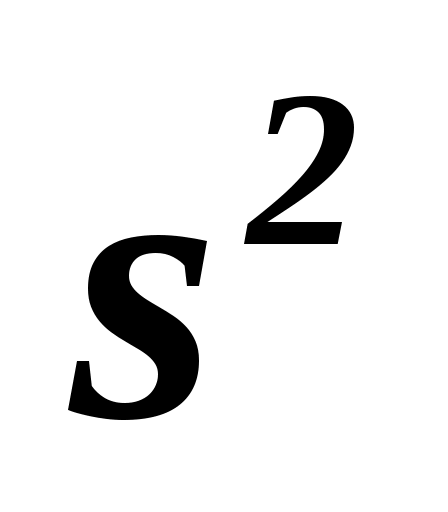 таблицы 1.1 – 1.3 дополним таблицей 1.4. таблицы 1.1 – 1.3 дополним таблицей 1.4.
Таблица 1.4

|
196
|
256
|
676
|
16
|
196
|
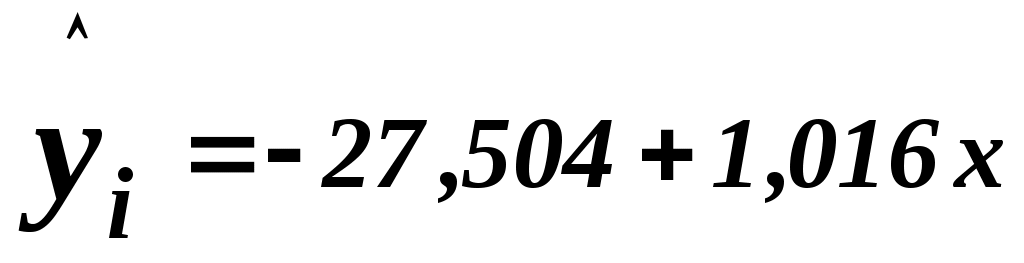
|
53,776
|
84,256
|
94,416
|
63,936
|
53,776
|
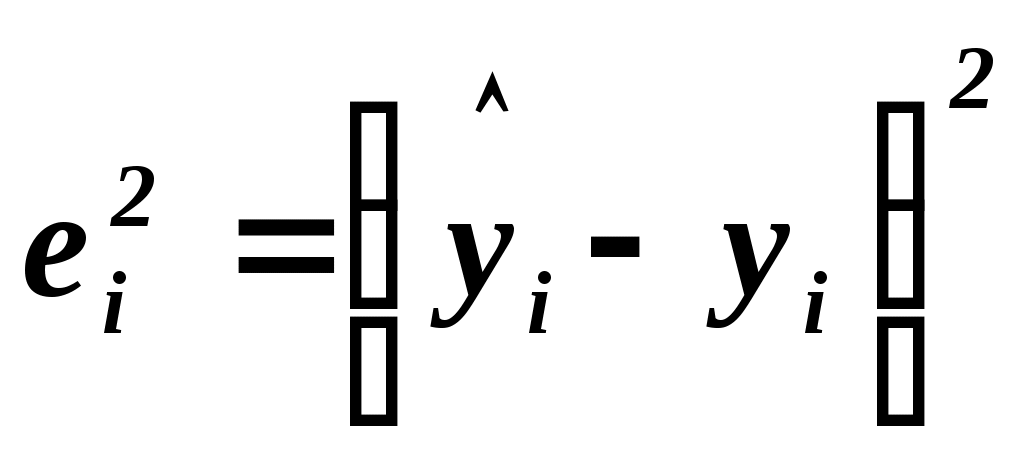
|
14,258
|
247,874
|
31,181
|
36,772
|
14,258
|
Продолжение таблицы 1.4.

|
196
|
16
|
16
|
196
|
676
|
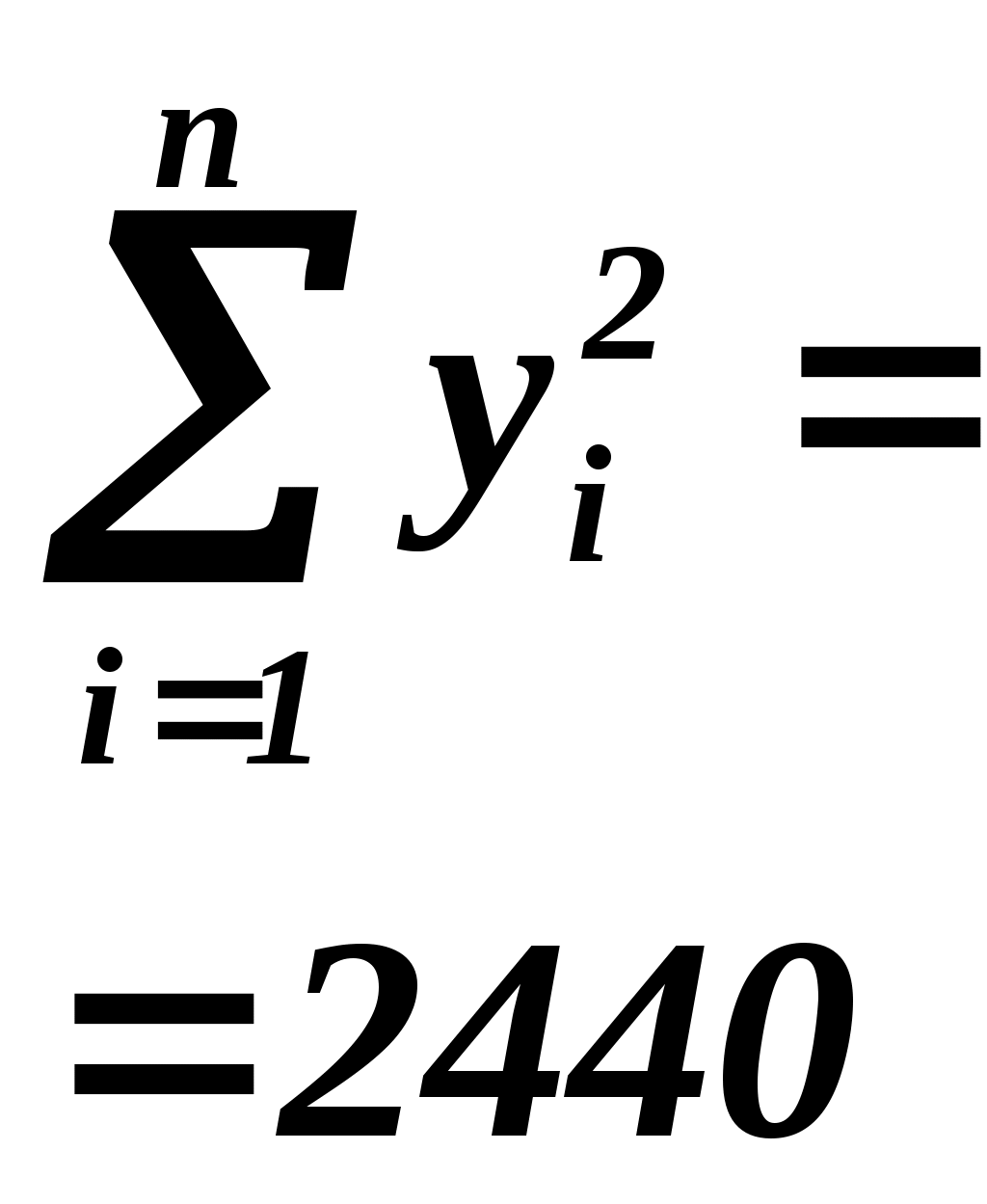
|
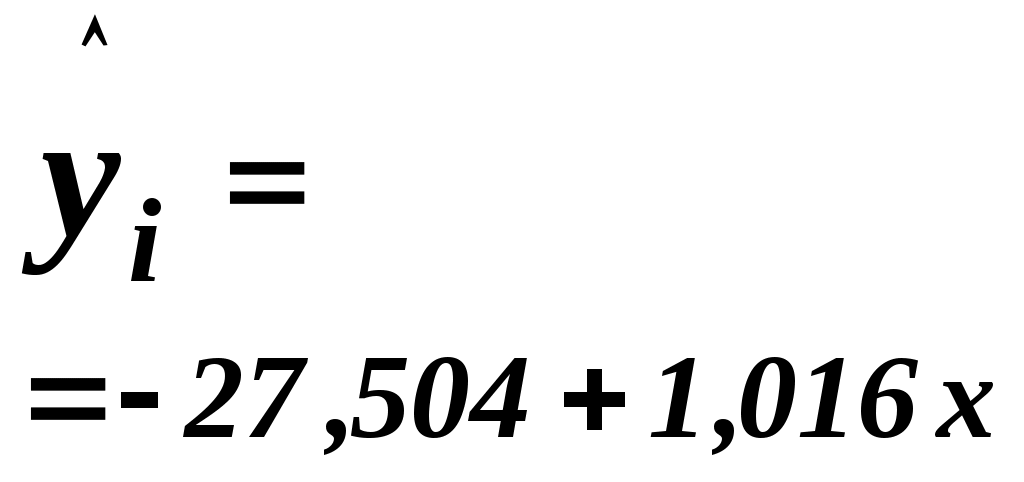
|
53,776
|
63,936
|
63,936
|
53,776
|
94,416
|
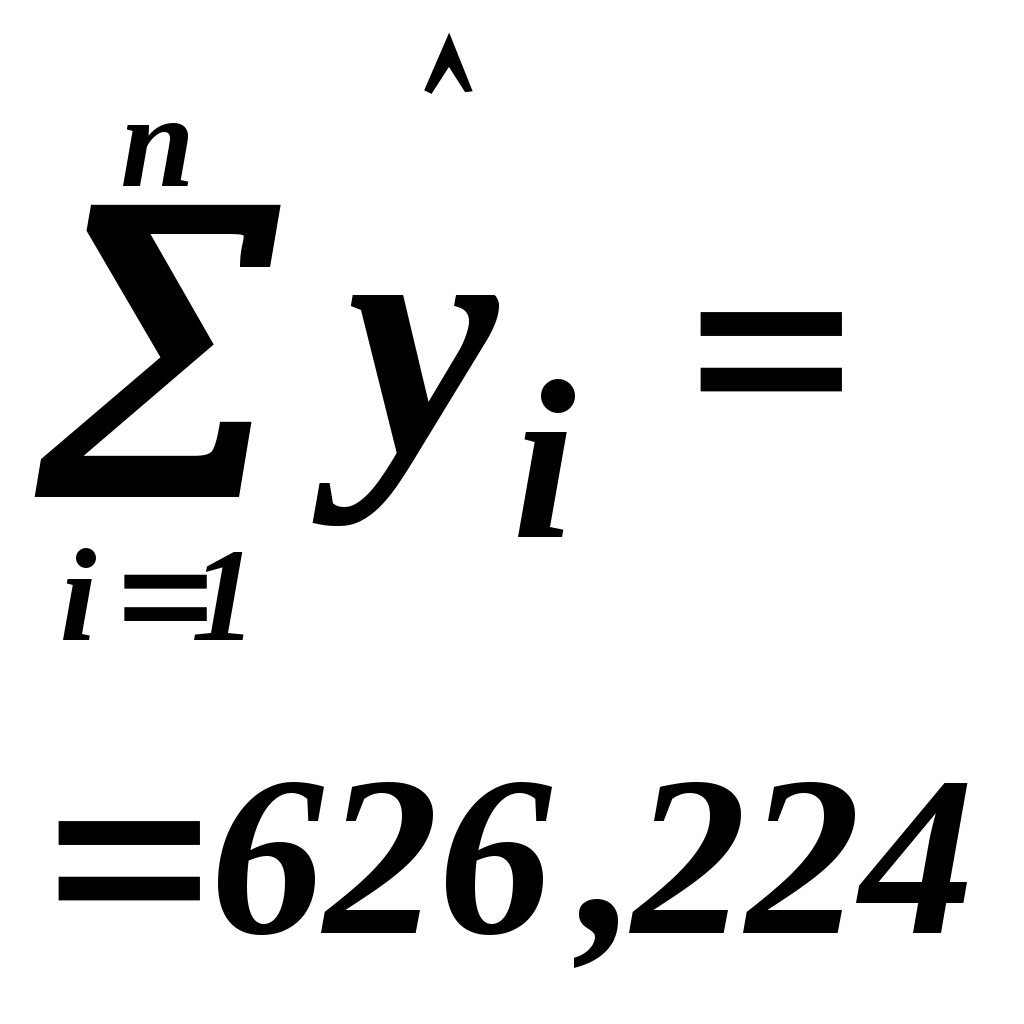
|
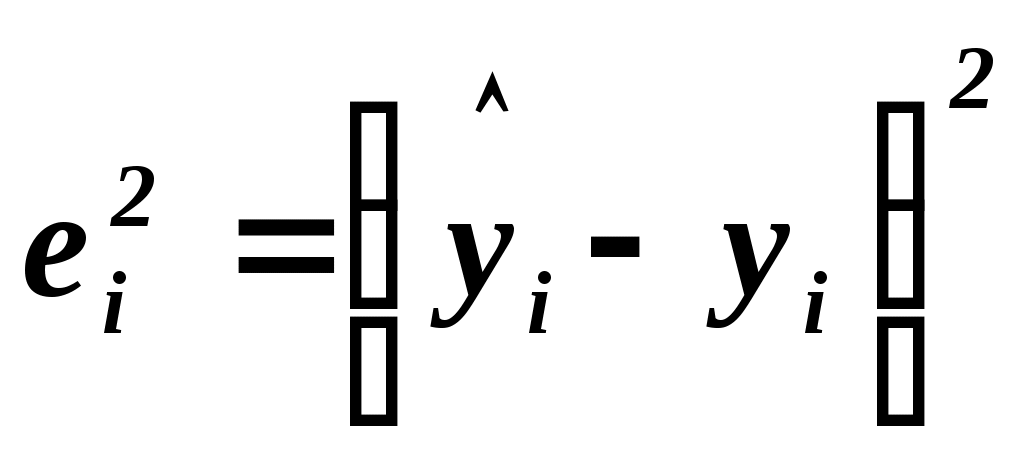
|
38,738
|
15,492
|
194,212
|
38,738
|
207,821
|
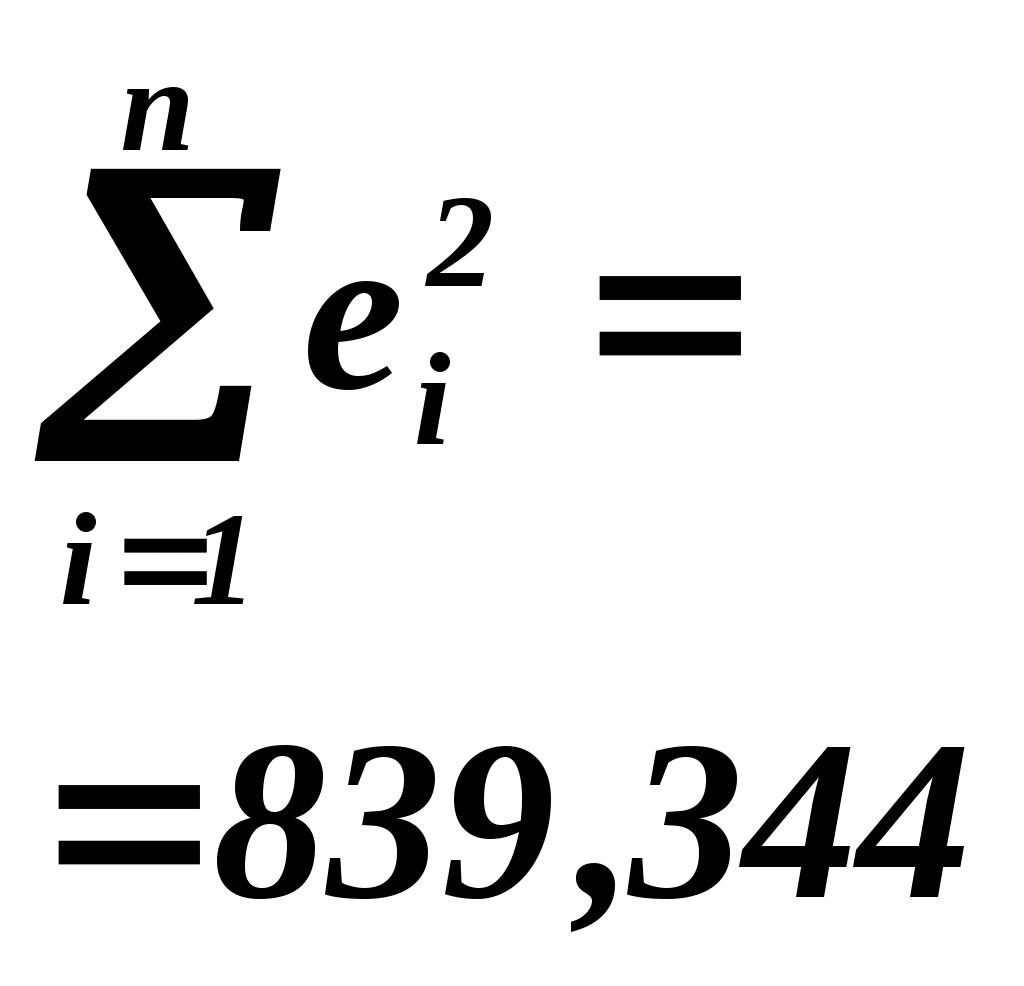
|
Выборочная остаточная дисперсия 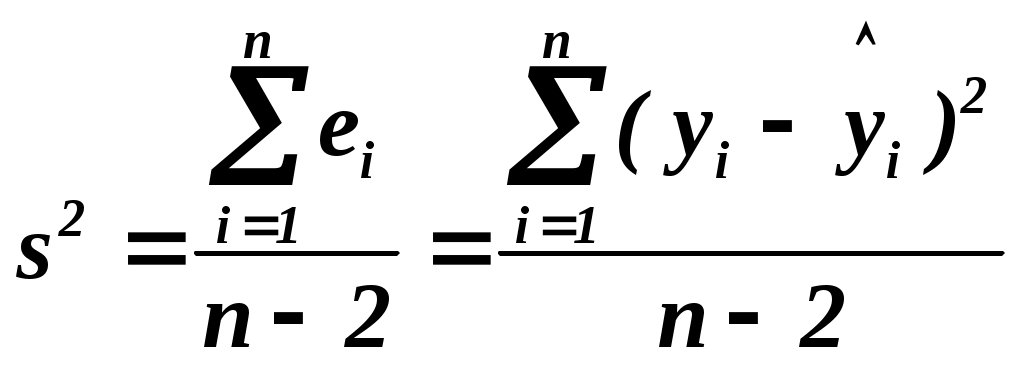 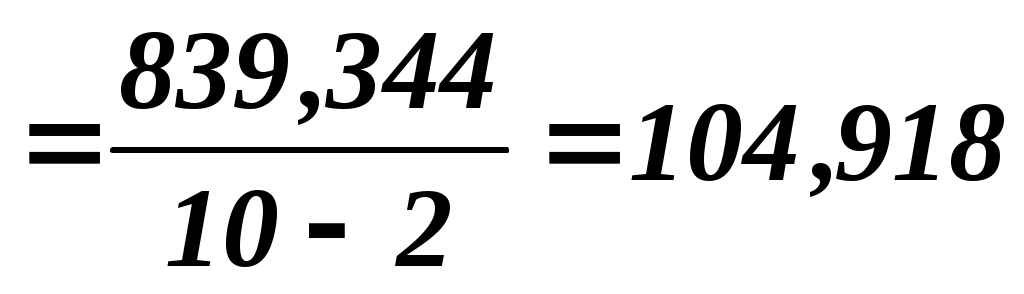 . Оценка дисперсии групповых средних . Оценка дисперсии групповых средних
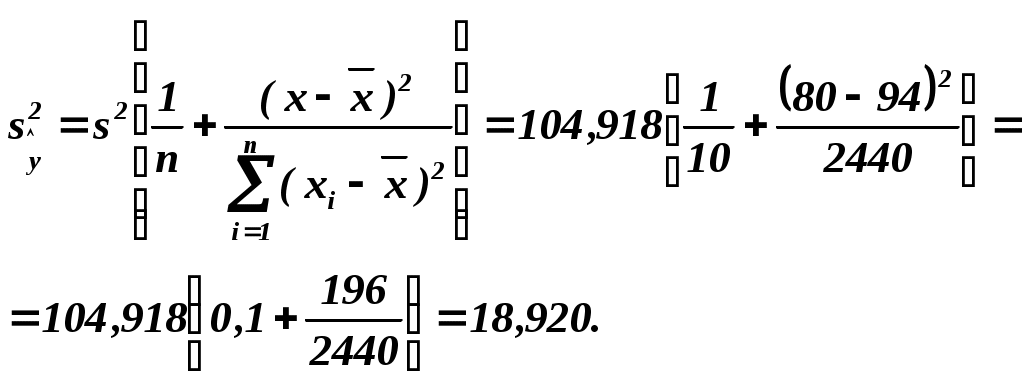  . .
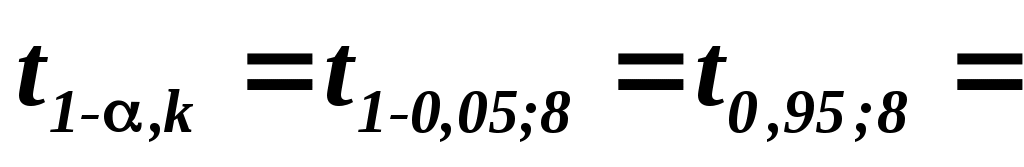  по таблице II приложений по таблице II приложений 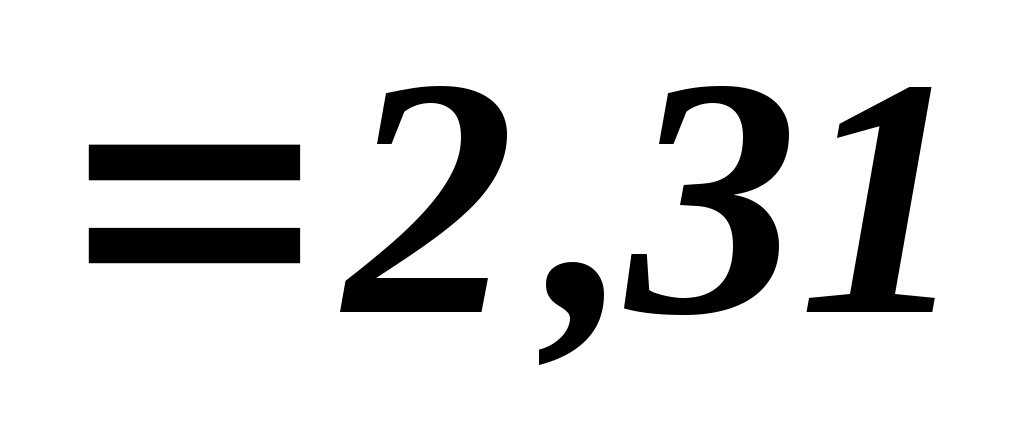 . .
.
Тогда доверительный интервал для 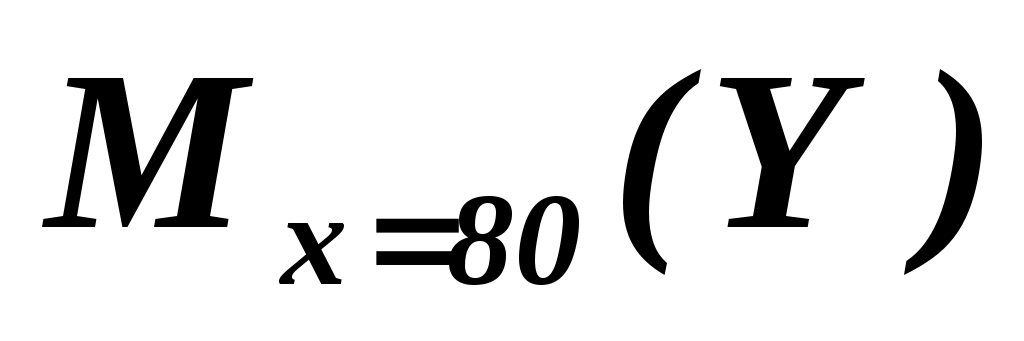 будет иметь вид: будет иметь вид:
 , или , или
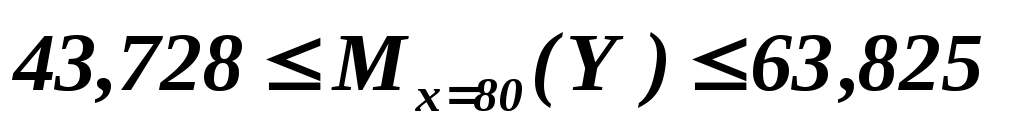 ( усл. ден. ед.). ( усл. ден. ед.).
Следовательно, среднее значение оценки компании с фактической стоимостью 80 усл. ден. ед.,, с надежностью 0,95 находится в пределах от 43,728 до 63,825 ( усл. ден. ед.).
5. Найти 95%-ный доверительный интервал для индивидуального значения оценки компании, фактическая стоимость которой составляет 80 усл. ден. ед.
 . Чтобы построить доверительный интервал для индивидуального значения . Чтобы построить доверительный интервал для индивидуального значения  , найдем дисперсию его оценки , найдем дисперсию его оценки 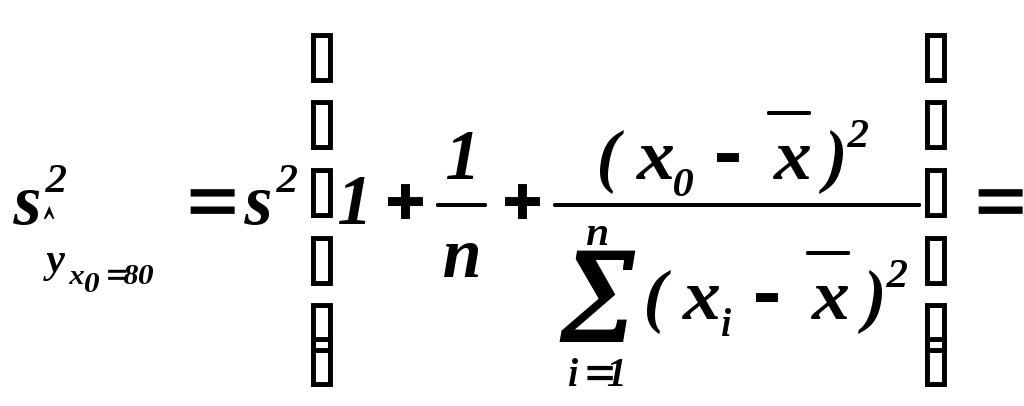
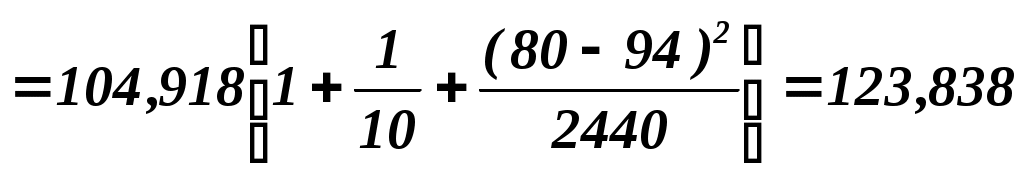 . .
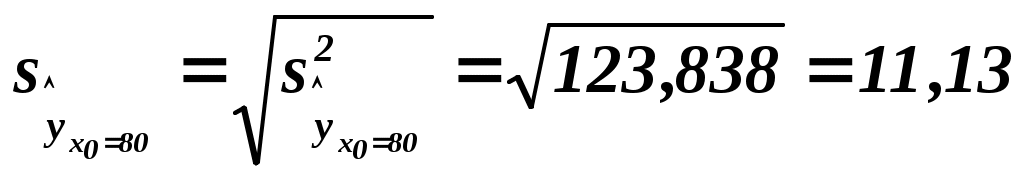 . .
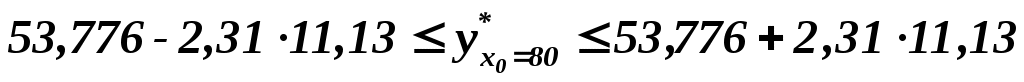 , или , или 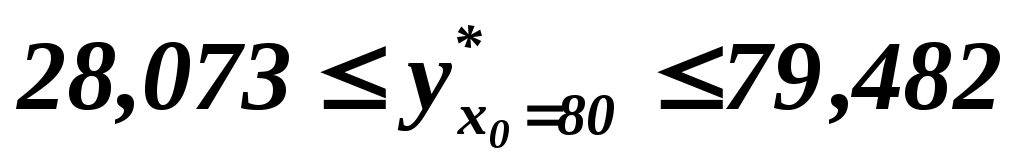 . Таким образом, индивидуальное значение оценки компании, фактическая стоимость которой составляет 80 усл. ден. ед., с надежностью 0,95 находится в пределах от 28,073 до 79,482 (усл. ден. ед.). . Таким образом, индивидуальное значение оценки компании, фактическая стоимость которой составляет 80 усл. ден. ед., с надежностью 0,95 находится в пределах от 28,073 до 79,482 (усл. ден. ед.).
|
 Скачать 1.62 Mb.
Скачать 1.62 Mb. .
.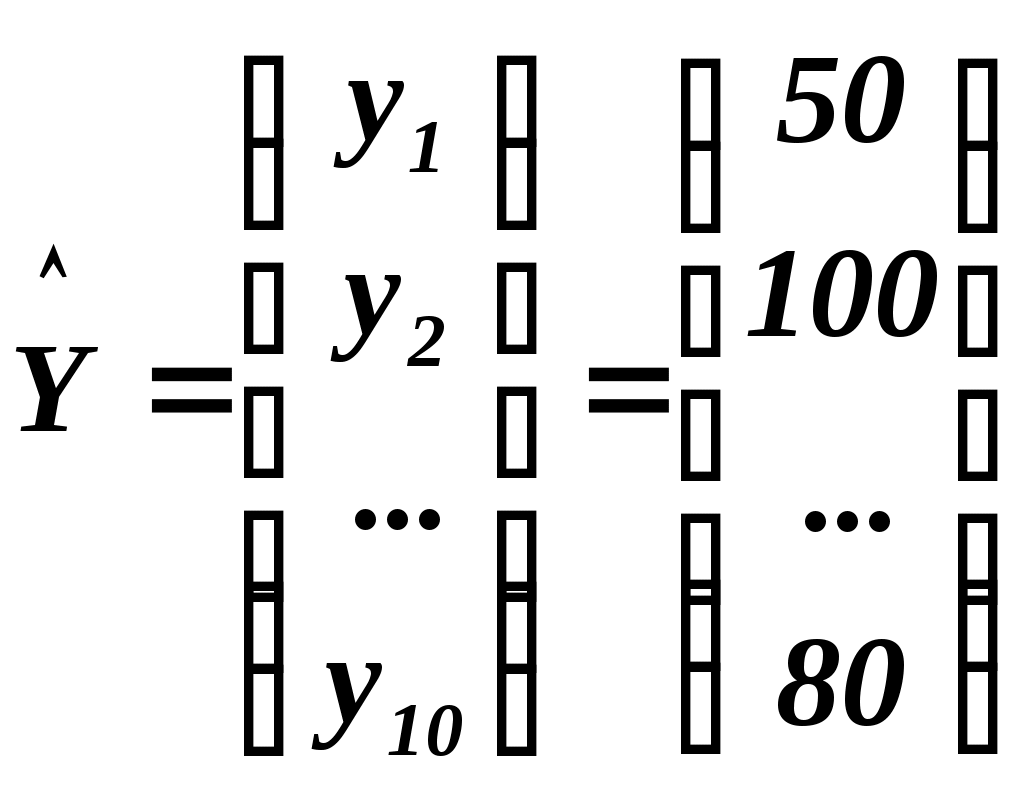 ,
, 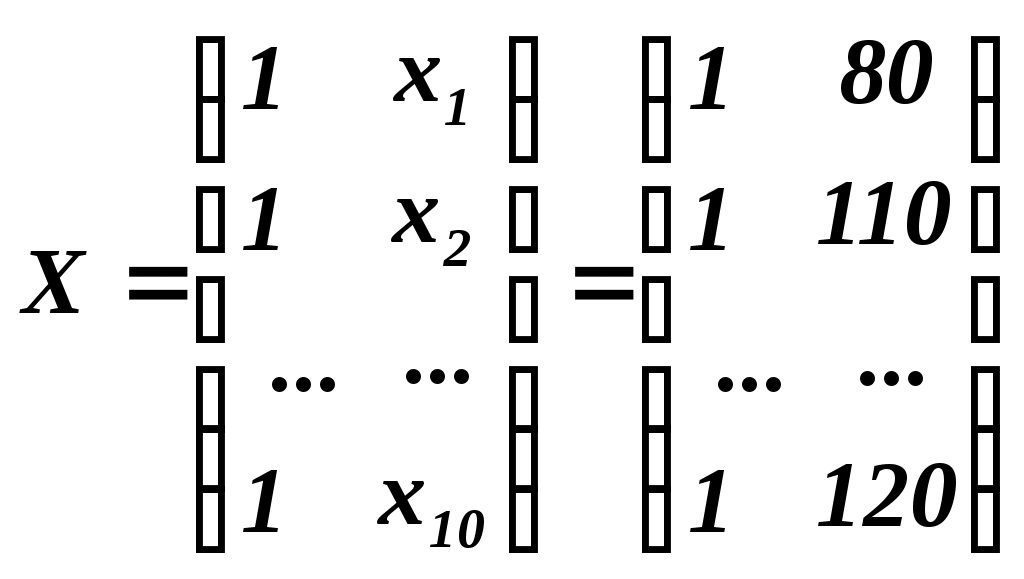 .
.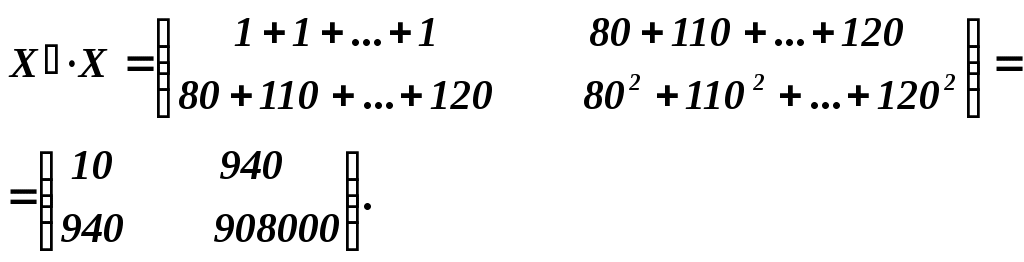
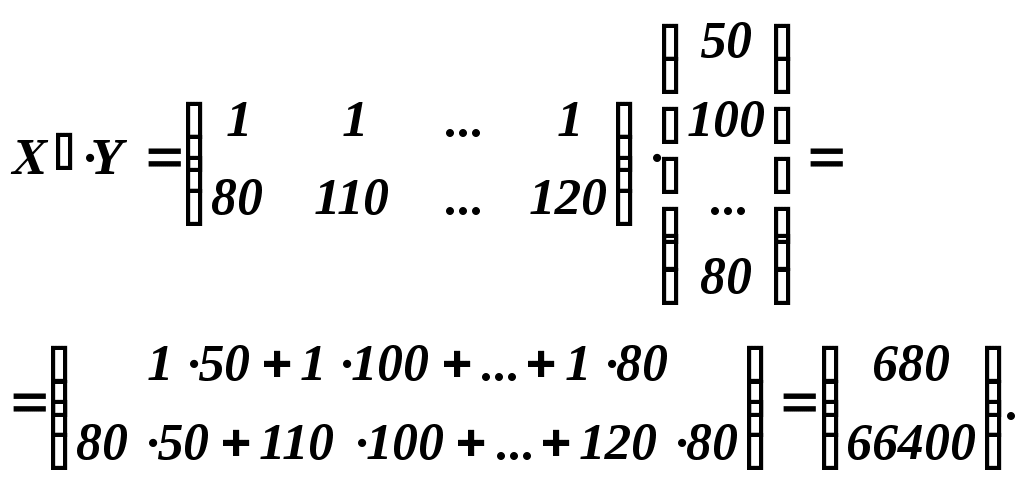
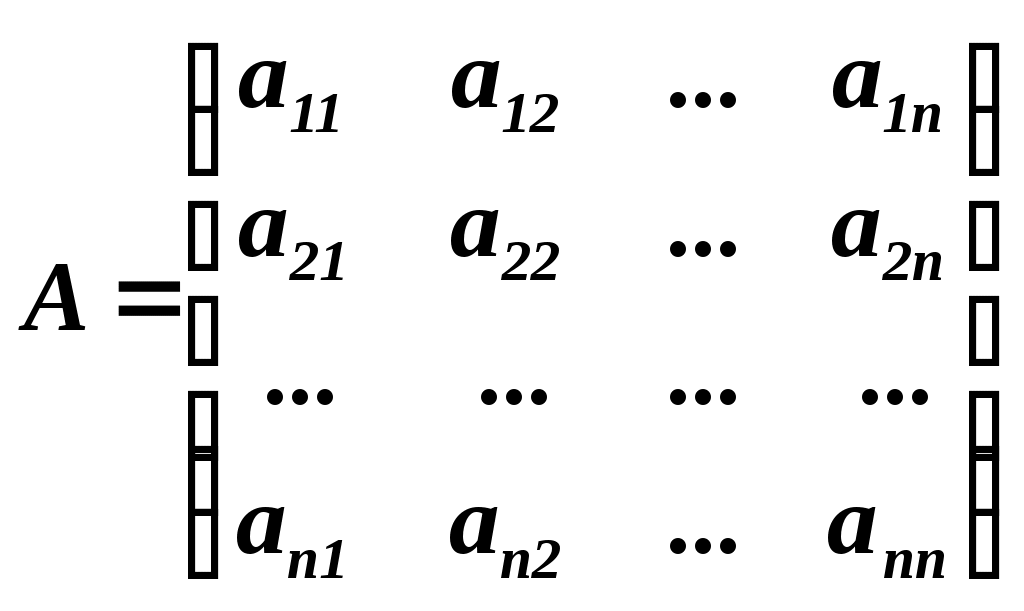 находится по формуле
находится по формуле 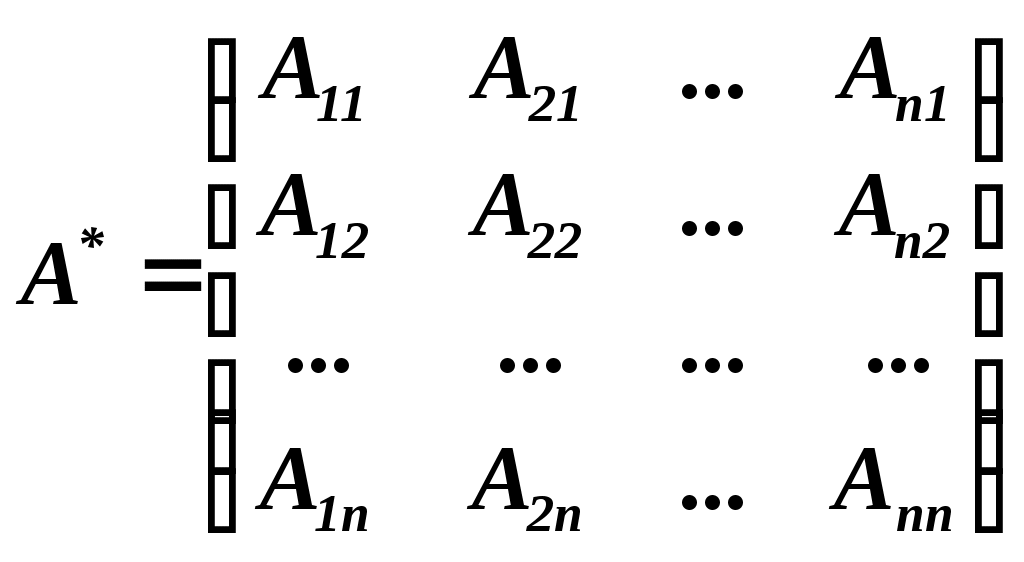 ).
).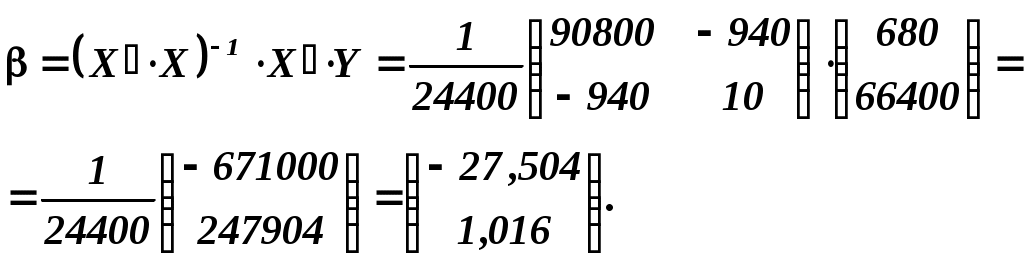
 .
.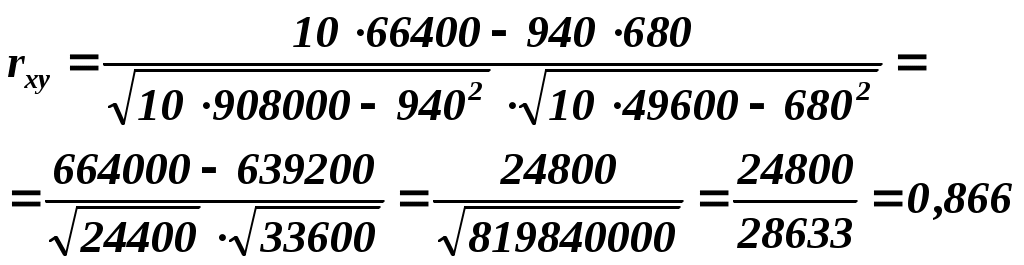 ,
,