Эконометрика. ЖданЧАСТЬ 1.1. Тема Парный регрессионный анализ
 Скачать 1.62 Mb.
|
|
1.2. Коэффициент детерминации Отношение регрессионной суммы квадратов 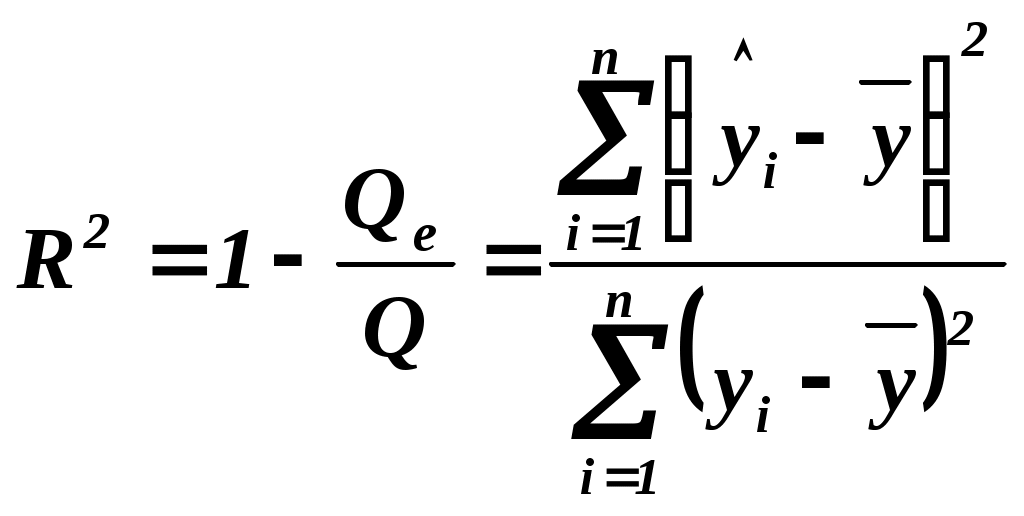 к общей сумме квадратов  называется коэффициентом детерминации (обозначается  ), т.е. = . означает долю общей дисперсии, объясненной регрессией  . Это мера качества подгонки регрессионной модели к наблюдаемым значениям.Уравнение регрессии значимо на уровне  , если фактически наблюдаемое значение статистики  фактич  ,где  - табличное значение - критерия Фишера-Снедекора, определенное на уровне значимости при  и  степенях свободы,  число параметров. Если наблюдаемое (фактическое) значение больше критического, то гипотеза отвергается и, следовательно, регрессия значима, а влияние фактора существенно на зависимую переменную.В случае линейной парной регрессии  , и уравнение регрессии значимо на уровне , если факт .Если известен коэффициент детерминации , то критерий значимости уравнения регрессии или самого коэффициента детерминации может быть записан в виде факт  .Значимость уравнения парной линейной регрессии может быть проверена и другим способом, если оценить значимость коэффициента регрессии  , который имеет  - распределение Стьюдента с  степенями свободы.Уравнение парной линейной регрессии, или коэффициент регрессии  , значим на уровне (иначе говоря, гипотеза  о равенстве параметра  нулю отвергается), если фактически наблюдаемое значение статистики  больше критического (по абсолютной величине), т.е.  tфакт  .1.3. Реализация линейной регрессии в Microsoft Excel Построение линейной регрессии (т.е. определение параметров  линейной регрессии  ) с помощью мастера функций fx, Статистические, ЛИНЕЙН.Первый способ Шаг 1. Введите исходные данные или откройте существующий файл, содержащий анализируемые данные; Шаг 2. Выделите область пустых ячеек 5x2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики. или область 1x2 — для получения только оценок коэффициентов регрессии; Шаг 3. Активизируйте Мастер функций любым из способов: а) в главном меню выберите Вставка/Функция; б) на панели инструментов Стандартная щелкните по кнопке Вставка функции; Шаг 4. В окне Категория (рис. 1.1) выберите Статистические, в окне Функция - ЛИНЕЙН. Щелкните по кнопке ОК; образом, если Константа = 0, то свободный член равен 0; 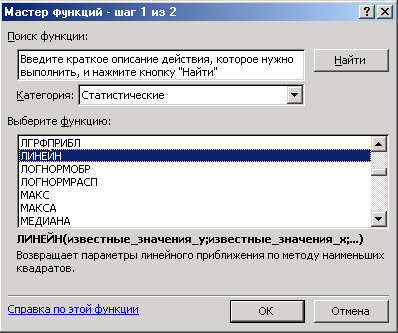 Рис. 1.1. Диалоговое окно «Мастер функций». Шаг 5. Заполните аргументы функции (рис. 1.2): Известные значения у - диапазон, содержащий данные результативного признака; Известные значения х - диапазон, содержащий данные факторов независимого признака; Константа - логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным Статистика - логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения. Щелкните по кнопке ОК; 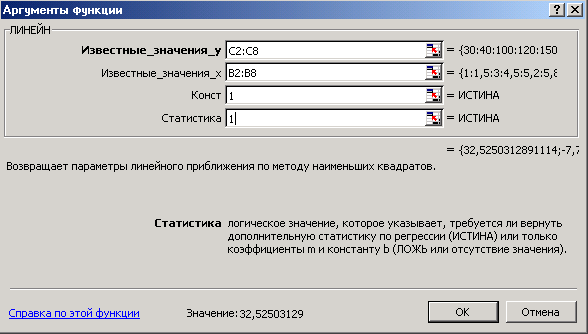 Рис. 1.2. Диалоговое окно ввода аргументов функции ЛИНЕЙН. Шаг 6. В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем на комбинацию клавиш CTRL+SHIFT+ENTER. Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. 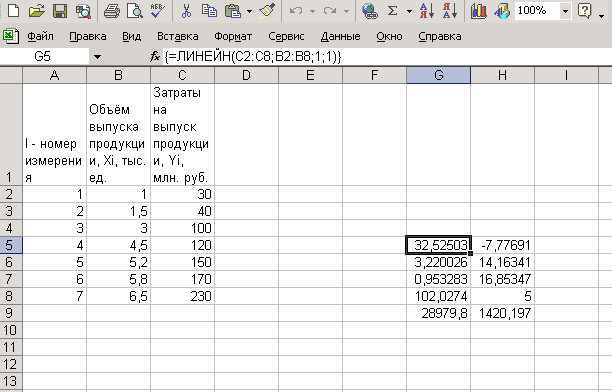 Рис. 1.3. Результат вычисления функции ЛИНЕЙН. Построение линейной регрессии с помощью инструментов Сервис, Анализ данных, Регрессия (Способ 2) С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий: Шаг 1. Активизируйте доступ к пакету анализа. В главном меню последовательно выберите Сервис /Надстройки. Установите флажок Пакет анализа (рис. 1.4);  Рис.1.4. Подключение надстройки Пакет анализа. Шаг 2. В главном меню выберите Сервис, Анализ данных, Регрессия. Щелкните по кнопке ОК; Шаг 3. Заполните диалоговое окно ввода данных и параметров вывода (рис. 1.5):  Рис. 1.5. Диалоговое окно ввода параметров инструмента Регрессия. Входной интервал У - диапазон, содержащий данные результативного признака; Входной интервал X- диапазон, содержащий данные факторов независимого признака; Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет; Константа - ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении; Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона; 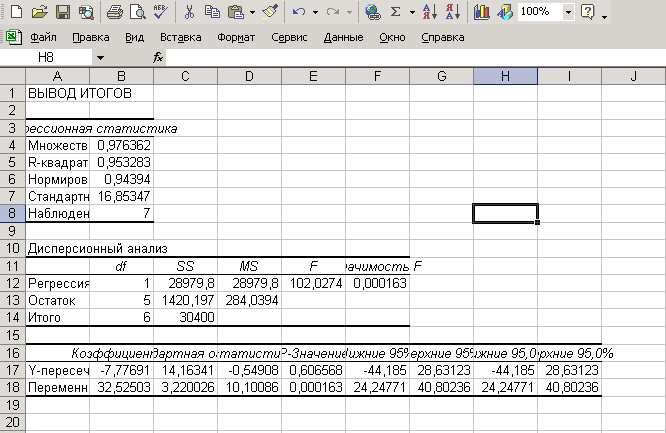 Рис. 1.6. Результаты регрессионного анализа Новый рабочий лист - можно задать произвольное имя нового листа. Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке ОК. Индивидуальное задание № 1 (ИЗ 1) Линейная парная регрессия Задание. Данные о фактической стоимости 10 нефтяных компаний (X, усл. ден. ед.) и оценке этих компаний оценочной фирмой (Y, усл. ден. ед.) приведены по вариантам в таблице 1.5. Требуется найти: 1. Уравнение регрессии Yпо X[а) эмпирическое уравнение регрессии, б) уравнение регрессии в отклонениях, в) уравнение регрессии в матричной форме]; Вычислить коэффициент корреляции между переменными Y и X; Проверить значимость коэффициента корреляции между переменными Y и X на уровне значимости = 0,05;Оценить среднее значение оценки компании с фактической стоимостью 80 усл. ден. ед.; Найти 95%-ные доверительные интервалы для среднего и индивидуального значений оценки компаний, фактическая стоимость которых составила 80 усл. ден. ед.; Найти с надежностью 0,95 интервальные оценки коэффициента регрессии и дисперсии  ;Оценить на уровне = 0,05 значимость уравнения регрессии Yпо X;Найти коэффициент детерминации и пояснить его смысл. Пример решения типового варианта ИЗ 1 Таблица 1.1
Для приведенных в таблице 1.1 данных о фактической стоимости 10 нефтяных компаний (X, усл. ден. ед.) и оценке этих компаний оценочной фирмой (Y, усл. ден. ед.) найдем: 1. а). Эмпирическое уравнение регрессии Y по X. Общий вид уравнения парной регрессии 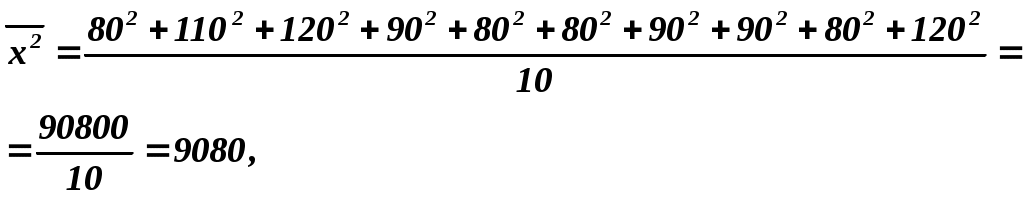 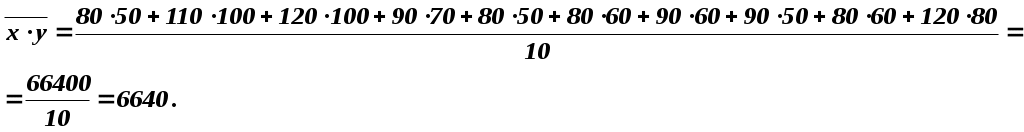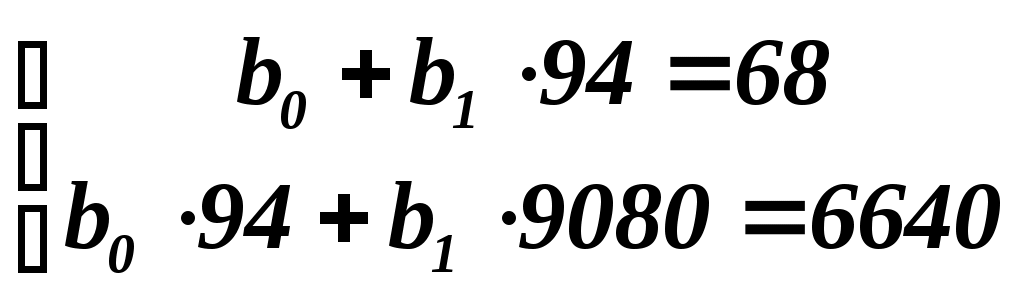. Для нахождения  и  используем метод наименьших квадратов.  ,  ,    . Следовательно,  = 68 - 94 . Тогда (68-94 )94 + 9080 = 6640, откуда = 1,016. Подставим найденное в равенство = 68 - 94 , получим: = - 27,504.Значит, эмпирическое уравнение регрессии Yпо X будет иметь вид:  . Из полученного уравнения следует, что при увеличении фактической стоимости компанииXна1 усл. ден. ед. значение оценки компании увеличивается в среднем на 1,016 усл. ден. ед. Свободный член (- 27,504) в данном уравнении регрессии не имеет реального смысла. |
.
