Эконометрика. ЖданЧАСТЬ 1.1. Тема Парный регрессионный анализ
 Скачать 1.62 Mb.
|
 .Линеаризованное уравнение будет иметь вид:  .Перейдем к исходным переменным  и  , выполнив потенцирование данного уравнения:  .Индекс корреляции:  .Связь между показателем и фактором можно считать тесной. Коэффициент детерминации:  .Вариация результата (себестоимость единицы продукции) на 82,88% объясняется вариацией фактора (объемом производства). Так как  ,то уравнение регрессии с вероятностью 0,95 в целом статистически значимое. Средняя относительная ошибка аппроксимации:  .В среднем расчетные значения отклоняются от фактических для показательной модели на 5,9 %. 4. Построение гиперболической модели парной регрессии Уравнение равносторонней гиперболы:  . Произведем линеаризацию модели путем замены X = 1/x. Тогда  . Рассчитаем параметры уравнения по данным таблицы 2.4. Таблица 2.4
В качестве значений переменных для функции ЛИНЕЙН – диапазоны, содержащие переменные  и . При построении функции ЛИНЕЙН укажем СТАТИСТИКА=0, так как нам достаточно знать только значения коэффициентов уравнения регрессии.  ;Действуя, как и в трех предыдущих случаях, получим: Уравнение гиперболической модели:  . ;Вариация результата на 83,62% объясняется вариацией фактора . .Уравнение статистически значимо, и в среднем расчетные значения отклоняются от фактических на 6,03 %. III. Для выбора лучшей модели построим сводную таблицу результатов 2.5. Таблица 2.5
Все модели имеют примерно одинаковые характеристики, но большее значение F-критерия Фишера и большее значение коэффициента детерминации R2 имеет гиперболическая модель. Ее можно взять в качестве лучшей для построения прогноза. IV. Расчет прогнозного значения результативного показателя Прогнозное значение результативного признака (себестоимость единицы продукции) определим по уравнению гиперболической модели, подставив в него планируемую, то есть заданную по условию, величину объема производства:  (тыс.руб.)V. Построим сначала диаграмму исходных данных. Для этого с помощью Вставка/Диаграмма активизируем Мастер Диаграмм и выполним 4 шага: 1 шаг. Выбор типа и вида диаграммы. Мы выбираем точечную диаграмму, которая позволяет сравнивать пары отрезков:  Рис 2.1 Тип диаграммы. 2 шаг. Источники данных. Во вкладке Диапазон указываем ячейки, содержащие исходные данные значений и . Во вкладке Ряд указываем в качестве Имени «исходные данные».  Рис 2.2 Источник данных диаграммы. 3 шаг. Параметры диаграммы. Здесь мы можем задавать заголовки, подписи данных. В нашем примере включим подписи осей:  Рис 2.3 Параметры диаграммы. 4 шаг. Размещение диаграммы. После нажатия Готово, диаграмма появляется в выбранном на шаге 4 диапазоне. На диаграмме, поместив мышь на ось X и нажав правую кнопку, мы сможем поменять формат оси. Мы выбрали минимальное и максимальное значения по оси, цену основных делений:  Рис 2.4 Формат оси. Аналогично поступаем с осью y. В готовой диаграмме исходных данных наведем мышь на точку исходных данных и в контекстном меню выберем Добавить линию тренда. В качестве Типа выбрать Степенная, во вкладке Параметры выделить «показывать уравнение на диаграмме и величину  » В результате получим: Рис 2.5 Степенной тренд. Аналогично строимм диаграмму для показательной модели. 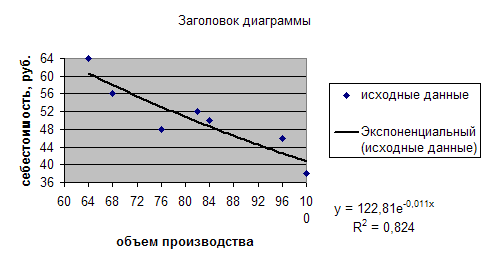 Рис 2.6 Экспоненциальный (потенциальный) тренд. Гиперболическая модель не является стандартной,поэтому диаграмму для нее нельзя построить, добавляя линию тренда. Вернемся к диаграмме исходных данных. Во вкладке Ряд используем команду Добавить. В качестве значений X и Y указываем диапазоны данных для x и  из таблицы 2.4.  Рис. 2.7 Добавление гиперболического тренда. Даем имя ряду: «гиперболическая модель». Далее шаг 3 и шаг 4 Мастера Диаграмм проделываем аналогично. В готовой диаграмме наведем мышь на точку исходных данных и в контекстном меню выберем Изменить тип диаграммы. Выбираем точечную диаграмму со значениями, соединенную линиями. В результате получим диаграмму: 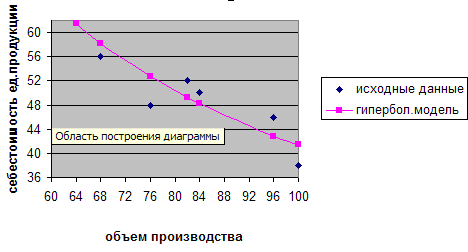 Рис 2.8 Гиперболический тренд. Варианты исходных данных ИЗ 2 |
