Эконометрика. ЖданЧАСТЬ 1.1. Тема Парный регрессионный анализ
 Скачать 1.62 Mb.
|
|
Итак, b = - 0,8923, A = 3, 3995. Видим, что для линеаризованного уравнения  . Получим линейное уравнение: Y = 3, 3995 – 0, 8923 X. Перейдем к исходным переменным  и  , выполнив потенцирование данного уравнения:  . Уравнение степенной модели регрессии:  .(Заметим, что для вычисления значения степени воспользовались функцией СТЕПЕНЬ(число; степень)). Подставляя в данное уравнение фактические значения 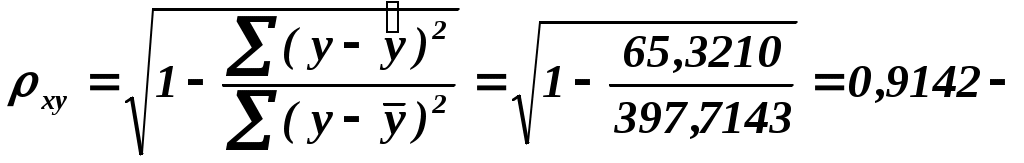, получим теоретические значения результата  . По ним рассчитаем показатели тесноты связи – индекс корреляции  и среднюю относительную ошибку аппроксимации  с помощью данных таблицы 2.2. Индекс корреляции:  cвязь между показателем и фактором можно считать достаточно сильной. Коэффициент детерминации:  .Вариация результата (себестоимость единицы продукции) на 83,5% объясняется вариацией фактора (объемом производства). Оценка значимости уравнения регрессии с помощью F-критерия Фишера: 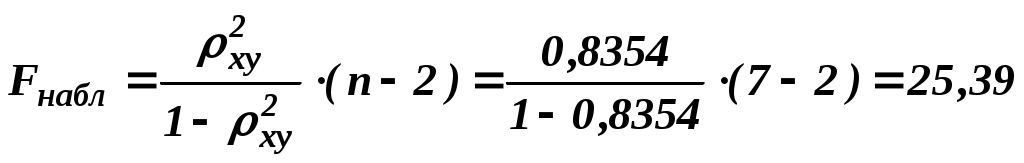 . ,то есть уравнение регрессии с вероятностью 0,95 в целом статистически значимое. Средняя относительная ошибка аппроксимации:  .В среднем расчетные значения отклоняются от фактических для степенной модели на 6,04%. 3. Построение показательной модели парной регрессии Уравнение показательной кривой:  .Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:  ; ,где  ,  ,  . Для расчетов используем данные таблицы 2.3.Таблица 2.3
В качестве значений переменных для функции ЛИНЕЙН – диапазоны, содержащие переменные и . Массив данных дополнительной регрессионной статистики имеет вид:
|
