Эконометрика. ЖданЧАСТЬ 1.1. Тема Парный регрессионный анализ
 Скачать 1.62 Mb.
|
|
ТЕМА 2. Нелинейные модели регрессии Нелинейная парная регрессия Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций регрессии. Нелинейные регрессии бывают 2 типов. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. Например,  - парабола второй степени, - равносторонняя гипербола.Регрессии, нелинейные по оцениваемым параметрам. Их можно разделить на внутренне линейные (которые с помощью соответствующих преобразований могут быть приведены к линейному виду) и внутренне нелинейные. Например,  - степенная, - показательная, - экспоненциальная.Парабола второй степени целесообразна к применению, если меняется характер связи признаков: прямая связь меняется на обратную связь или наоборот; и определяется максимальное или минимальное значение результативного признака. Параметры уравнения оцениваются с помощью МНК и находятся из системы нормальных уравнений: 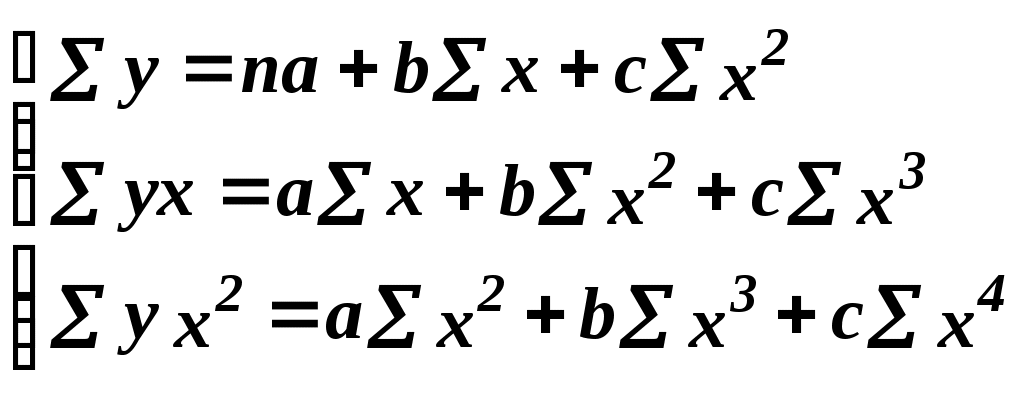 В виду симметричности парабола второй степени не всегда пригодна в конкретных исследованиях. Равносторонняя гипербола применяется для характеристики связи удельных расходов сырья, материалов, топлива и т. д. Для оценки параметров применяется МНК к линеаризованному уравнению  , где  - новая переменная.В уравнении степенной регрессии параметр b имеет четкое экономическое истолкование – коэффициент эластичности. (Коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид:  Для оценки параметров применяется МНК к линеаризованному уравнению  , где .Для линеаризации уравнения показательной регрессии производятся замены  И тогда  - линейное уравнение.Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора  , то обычно рассчитывается средний коэффициент эластичности: .Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах. Отметим, что тесноту связи изучаемых явлений для нелинейной регрессии оценивает индекс корреляции: 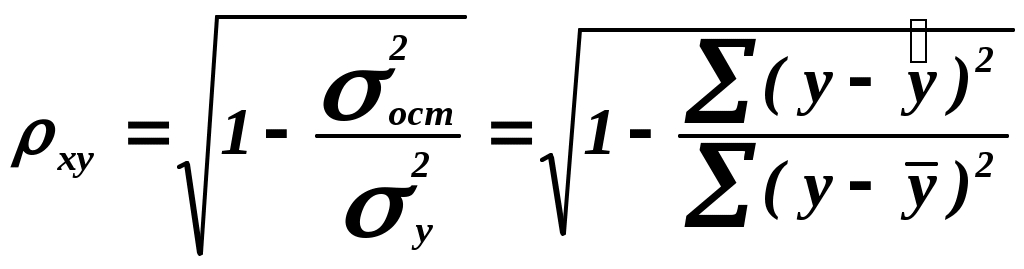 , где - общая дисперсия результативного признака y; - остаточная дисперсия, определяемая исходя из уравнения регрессии. Индивидуальное задание № 2 (ИЗ 2) Построение моделей нелинейной парной регрессии Задание. По семи предприятиям тяжелой промышленности региона получена информация, характеризующая зависимость себестоимости единицы продукции (Y, тыс. руб.) от объема производства (X, млн. руб.). Данные приведены таблице 2.6. Требуется: I . Для характеристики зависимости Y от X построить следующие модели: 1. линейную (для сравнения с нелинейными), 2. степенную, 3. показательную, 4. гиперболическую. II. Оценить каждую модель, определив: 1. индекс корреляции, 2. среднюю относительную ошибку аппроксимации, 3.коэффициент детерминации, 4. F-критерий Фишера. III. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик. IV. Рассчитать прогнозные значения результативного признака по лучшей модели, если объем производства составит 89,573 млн. руб. V. Результаты расчетов отобразить на графике. Пример решения типового варианта ИЗ 2 По семи предприятиям тяжелой промышленности региона получена информация, характеризующая зависимость себестоимости единицы продукции (y, тыс.руб.) от объема производства (x, млн. руб.).
I., II. 1. Построение линейной модели парной регрессии Воспользуемся данными таблицы 2.1. Таблица 2.1
Приведем данные дополнительной регрессионной статистики, полученной с помощью встроенной функции ЛИНЕЙН (см. тему «Парная регрессия»):
|
