КР инф.техн.. Тема предмет и метод статистики. Сводка и группировка задача
 Скачать 91.44 Kb. Скачать 91.44 Kb.
|
|
ТЕМА 1. ПРЕДМЕТ И МЕТОД СТАТИСТИКИ. СВОДКА И ГРУППИРОВКА Задача. По ряду предприятий легкой промышленности получены данные, представленные в таблице. Произведите группировку предприятий по размеру основных средств, образуя 6 групп с равными интервалами. По каждой группе подсчитайте: число предприятий объем основных средств средний размер основных средств одного предприятия объем произведенной продукции выпуск продукции на 1000 рублей основных средств
Результаты расчета оформите в таблицы. Сделайте выводы. Решение: Группировка – это разбиение совокупности на группы, однородные по какому-либо признаку. С точки зрения отдельных единиц совокупности, группировка – это объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам. По условиям задачи необходимо провести группировку предприятий по размеру основных средств, образуя 6 групп с равными интервалами. Интервал очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе.Формулы для вычислений размера интервала: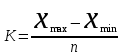 , где , гдеxmax максимальное значение факторного признака в совокупности; xmin – минимальное значение факторного признака в совокупности; n - число групп. В случае равных интервалов величина интервала может быть определена как: К = 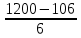 = 182,33 тыс.руб. = 182,33 тыс.руб.Определяем границы групп: 1. 106+182,33=288,33 2. 288,33+182,33=470,67 3. 470,67+182,33=653 4. 653+182,33=835,33 5. 835,33+182,33=1017,67 6. 1017,67+182,33=1200 Исходя из расчетов, группировка будет содержать 6 групп предприятий по размеру основных средств с равными интервалами: 1 гр.: от 106 до 288,33 тыс.руб. 2 гр.: от 288,33 до 470,67 тыс.руб. 3 гр.: от 470,67 до 653,00 тыс.руб. 4 гр.: от 653,00 до 835,33 тыс.руб. 5 гр.: от 835,33 до 1017,67 тыс.руб. 6 гр.: от 1017,67 до 1200 тыс.руб. Группировка предприятий по размеру основных средств представлена в таблице 1. По каждой группе подсчитаны: 1. число предприятий 2. объем основных средств 3. средний размер основных средств одного предприятия 4. объем произведенной продукции 5. выпуск продукции на 1000 рублей основных средств Таблица 1- Группировка предприятий по размеру основных средств
Вывод: как показали расчеты, в данной совокупности преобладают предприятия с величиной основных средств от 106 до 288,33 тыс. руб. – 14 предприятий. Средний размер основных средств на 1 предприятие в данной группе составляет 202,36 тыс.руб., выпуск продукции на 1000 рублей основных средств в данной группе 1408,40 тыс.руб. В целом, по группе предприятий средний размер основных средств на 1 предприятие составляет 423,80 тыс.руб., выпуск продукции на 1000 рублей основных средств 1090,14 тыс.руб. ТЕМА 2. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ Задача. Натуральный баланс сахара в регионе характеризуется следующими данными, млн. тонн:
Определить: 1) запасы сахара на конец года; 2) соотношение потребленного и вывезенного сахара; 3) структуру потребления. Решение: 1) Расчет запасов сахара на конец года производится по формуле: Зсах.(к.г.)= Зсах.(н.г.)+ Прсах.- Птсах.-Всах где Зсах.(к.г.) - запасы сахара на конец года; Зсах.(н.г.) - запасы сахара на начало года; Прсах. – произведено сахара за год; Птсах. – потреблено сахара за год; Всах- вывоз сахара за пределы региона. Зсах.(к.г.)= 2,2+23,4-16,6-7,0=2,0 млн. тонн. Запасы сахара на конец года составили 2,0 млн. тонн. 2) Соотношение потребленного и вывезенного сахара: СПт/В= Птсах./Всах. СПт/В= 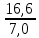 = 2,4 = 2,4Соотношение потребленного и вывезенного сахара составило 2,4:1- т.е., потреблено сахара в 2,4 раза больше, чем вывезено. 3) Структуру потребления следует рассчитать на основании расчета относительной величины структуры (доли отдельных частей изучаемой совокупности во всем ее объеме) – делением числа единиц в отдельных частях совокупности на общее число единиц совокупности Доля производственного потребления: Дпроиз.пт.=Пт(произ.пт.)сах./ Птсах.*100% Дпроиз.пт.= 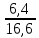 *100%=38,55% *100%=38,55%Доля потребления населением: Днас.пт.=Пт(нас.пт.)сах./ Птсах.*100% Дпроиз.пт.= 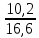 *100%=61,45% *100%=61,45%Структуру потребления представим в виде таблицы 1. Таблица 1 - Структуру потребления
Вывод: таким образом, в регионе 61,45% сахара потребляется населением региона и только 38,55% - составляет производственное потребление. ТЕМА 3. СРЕДНИЕ ВЕЛИЧИНЫЗадача. Имеются данные по 2-м заводам, вырабатывающим одноименную продукцию. Определить для каждого года отдельно средние затраты времени на единицу продукции по двум заводам вместе.
Решение: Расчет средних затрат времени на единицу продукции по двум заводам вместе в предыдущем году производится по формуле средней арифметической взвешенной: 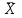 = =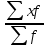 Обозначим для каждого завода количество продукции, тыс. шт.; Средние затраты времени на единицу продукции по двум заводам вместе в предыдущем году составили: 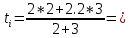 2,12 час 2,12 часСредние затраты времени на единицу продукции по двум заводам вместе в текущем году составили: t = 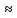 1,92 час. 1,92 час.Ответ:1,92 час. - затраты времени на единицу продукции по двум заводам вместе. ТЕМА 4. ПОКАЗАТЕЛИ ВАРИАЦИИЗадача. Имеются следующие данные о расходах граждан в январе условного года:
Определить: 1) среднедушевой расход городских и сельских жителей; 2) дисперсии душевого расхода: среднюю из групповых, межгрупповую, общую; 3) зависимость расходов от места жительства, исчислив коэффициент детерминации и эмпирическое корреляционное отношение. Решение: 1) среднедушевой расход городских и сельских жителей = (120*36)+(50*64)/100=(4320+3200)/100=75,2. 2) дисперсии душевого расхода: среднюю из групповых, межгрупповую, общую: Дисперсия внутригрупповая (город)=324. Дисперсия внутригрупповая (село)=196. Средняя дисперсия из внутригрупповых = (324*36)+(196*64)/100 = 242,08. Межгрупповая дисперсия 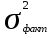 = = 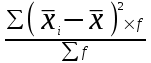 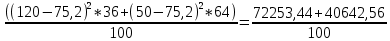 = = 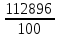 = = 1128,96 = = 1128,96Существует простая и важная формула, связывающая общую дисперсию, межгрупповую дисперсию и среднюю по внутригрупповым дисперсиям: 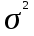 = =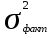 + +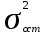 Общая дисперсия = 1128,96 + 242,08 = 1371,04 Коэффициент детерминации: 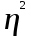 = =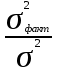 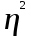 = 1128,96/1371,04 = 0,82 = 1128,96/1371,04 = 0,82Эмпирическое корреляционное отношение: 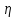 = =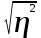 = =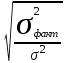 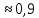 Вывод: значение коэффициента детерминации указывает, что на 82% уровень расходов жителей поселений зависит от их принадлежности к городским или к сельским жителям и только 17,7% вариации расходов определяются другими причинами. Эмпирическое корреляционное отношение достаточно близко к 1, что указывает на сильную связь расходов населения с местом их проживания. ТЕМА 5. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕЗадача. Для определения средней величины заработной платы работников малых предприятий необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество работников нужно отобрать, чтобы ошибка выборки с вероятностью 0,954 не превышала 2 тыс. руб. при среднем квадратическом отклонении 10 тыс. руб. Решение: Отсюда Следовательно: т.к. по условию σ = 10 и t = 2, при p = 0,954, то имеем n = 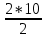 = 10 чел. = 10 чел.Вывод: необходимо отобрать 100 человек, чтобы ошибка выборки с вероятностью 0,954 не превышала 2 тыс. руб. при среднем квадратичном отклонении 10 тыс. руб. ТЕМА 6. РЯДЫ ДИНАМИКИ Задача. Имеется информация о списочном составе работников малого предприятия за октябрь месяц. На 1 сентября – 40 человек, 5 сентября уволилось 8 человек, 12 сентября принято 5 человек, 20 сентября уволилось 2 человека, 25 сентября принято 10 человек. Определить среднесписочный состав работников за сентябрь месяц. Решение: Среднесписочная численность работников определяется на основании данных о списочной численности. Среднесписочная численность работников за месяц исчисляется путем суммирования списочной численности работников за каждый календарный день месяца, то есть с 1-е по 30-е или 31-е число (для февраля - по 28-е или 29-е число), включая праздничные (нерабочие) и выходные дни, и деления полученной суммы на число календарных дней месяца. В данном случае в сентябре месяце 30 календарных дней. С 1-го по 4-е сентября (4 дня) работало 40 человек. С 5-го по 11-е сентября (7 дней) работало 32 человека. С 12-го по 19-е сентября (8 дней) работало 37 человек. С 20-го по 24-е сентября (5 дней) работало 35 человек. С 25-го по 30-е сентября (6 дней) работало 45 человек. Отсюда среднесписочный состав работников за сентябрь месяц равен Х ̅ = Х ̅ = 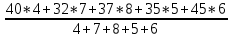 = = 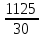 = 37,5 = 37,5Ответ: 38 человек - среднесписочный состав работников за сентябрь. ТЕМА 7. ЭКОНОМИЧЕСКИЕ ИНДЕКСЫЗадача. Денежные затраты на строительно-монтажные работы увеличились в текущем периоде на 38%, а себестоимость работ – на 46,8%. Определить индекс объема строительно-монтажных работ. Решение: Индекс объёма строительно-монтажных работ равен отношению индекса денежных затрат на строительно-монтажные работы к индексу себестоимости работ и равен Iq- индекс объема; Iq – индекс денежных затрат на строительно-монтажные работы; Iр – индекс себестоимости работ. Iq = 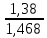 = 0,94 = 0,94Следовательно, объём строительно-монтажных работ в текущем периоде снизился на 6% (100%-94% = 6%). ТЕМА 8. ОСНОВЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА Задача. По 8 однородным магазинам имеются следующие данные:
Найдите уравнение корреляционной связи товарооборота и уровня издержек обращения. Вычислите коэффициенты эластичности, показатели тесноты корреляционной связи. Сделайте выводы. Решение: Парная линейная корреляционная связь характеризуется линейной регрессией решая систему линейных уравнений 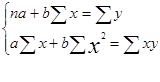 Обозначим товарооборот - х; уровень издержек обращение - у. Коэффициенты a, b регрессионной модели находим методом наименьших квадратов, решая систему линейных уравнений an+ b∑x= ∑y,a∑x+ b∑x2 = ∑yx, где n − число магазинов (для данной задачи n = 8). Для решения данной системы уравнений составим расчетную таблицу:
Подставим в систему уравнений найденные значения сумм: 8a +307b = 55, 307a + 21699b =1766,5. Решив данную систему, получим: b=(8*1766,5-55*307)/(8*21699-307*307)=(14132-16855)/(173592-94249)=-2723/79343=-0,035 а=55/8+0,035*(307/8)=6,875+0, 035*38,375=6,875+1,343=8,22 a = 8,22; b = -0,035 Отсюда выборочное уравнение регрессионной зависимости уровня издержек обращения Y от товарооборота Х имеет вид Подставляя в уравнение последовательно значение х, получаем выровненные (теоретические) значения результативного показателя ух. Для измерения тесноты связи вычислим коэффициент корреляции:
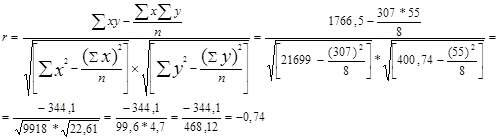 В данном случае коэффициент корреляции является отрицательным, это говорит о том, что получилась отрицательная корреляция - корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной. Коэффициент эластичности - показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного на 1% Эx = а1 * (хср/уср) где xi - среднее значение соответствующего факторного признака; y - среднее значение результативного признака; a1 - коэффициент регрессии при соответствующем факторном признаке. Хср =307/8 = 38,38 Уср = 55/8 = 6,88 а1 = - 0,035 Эх = - 0,035*(38,38/6,88) = - 0,2 Вывод: при увеличении товарооборота уровень издержек снизится на 0,2%. ТЕМА 9. СТАТИСТИЧЕСКИЙ АНАЛИЗ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ ОБЩЕСТВА Задача. Имеются следующие условные данные о численности населения страны: На начало 2006 года численность оставляла 52755 тыс.чел., на начало 2007 года – 53115 тыс.чел. Коэффициенты рождаемости и смертности в 2006 году составили соответственно 15,3 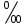 и 12,1 и 12,1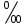 . .Определить коэффициент механического прироста населения. Сделать выводы. Решение: Средняя численность населения за 2006 год равна: S = ННГ+НКГ/2 S == 52755+53115/2 = 52935 тыс.руб. Определим коэффициент общего прироста населения как: 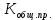 = НКГ-ННГ/S*1000 = НКГ-ННГ/S*1000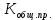 = 53115-52755/52935*1000 = 6,8% = 53115-52755/52935*1000 = 6,8%Коэффициент естественного прироста равен: 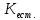 = = 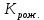 .– .–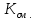 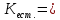 15,3 −12,1 = 3,2 % 15,3 −12,1 = 3,2 %Отсюда определим коэффициент механического прироста населения 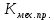 = = 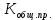 . − . − 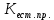 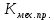 = 6,8 −3,2 = 3,6 % = 6,8 −3,2 = 3,6 %Вывод: прирост численности населения за 2006 год распределился примерно поровну между двумя факторами – естественным приростом и механическим приростом. ТЕМА 10. СТАТИСТИКА РЫНКА ТРУДА И ЗАНЯТОСТИ НАСЕЛЕНИЯ Задача. По предприятию за апрель имеются следующие данные (чел.дни): отработано - 2520, целодневные простои - 10; всего неявок 1070, в том числе в связи с праздничными и выходными днями - 960, очередными отпусками - 60. В феврале - 22 рабочих дня. Определите: 1) календарный, табельный и максимально возможный фонды рабочего времени; 2) среднесписочную численность и среднее явочное число работающих; 3) среднее число дней неявок в составе максимально возможного фонда рабочего времени в расчете на одного среднесписочного работника предприятия. Решение: 1) Определим календарный фонд рабочего времени по формуле: 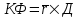 ; КФ= сумма явок и неявок. ; КФ= сумма явок и неявок.КФ = (2520+1070)*22 = 78980 чел.дней Определим табельный фонд рабочего времени: ТФВ=КФ - неявки в выходные и праздничные дни ТФВ = 78980 - 960 = 78020 чел. дней Определим максимально возможный фонд рабочего времени: МВФ=КФ - неявки (праздничные и выходные) - неявки из-за очередных отпусков МВФ = 78020 - 60 = 77960 чел. дней 2) Определим среднесписочную численность: Определим среднеявочную численность: 3) Определим среднее число дней неявок в составе максимально возможного фонда рабочего времени в расчете на одного среднесписочного работника предприятия: Среднее число дней неявок = Среднее число дней неявок/ССЧ Среднее число дней неявок = 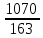 = 7. = 7.Ответ: КФ=78980 чел.дней, ТФВ = 78020 чел. дней, МВФ = 77960 чел. дней; среднесписочную численность = 163 чел., среднеявочную численность = 115 чел., среднее число дней неявок = 7. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
