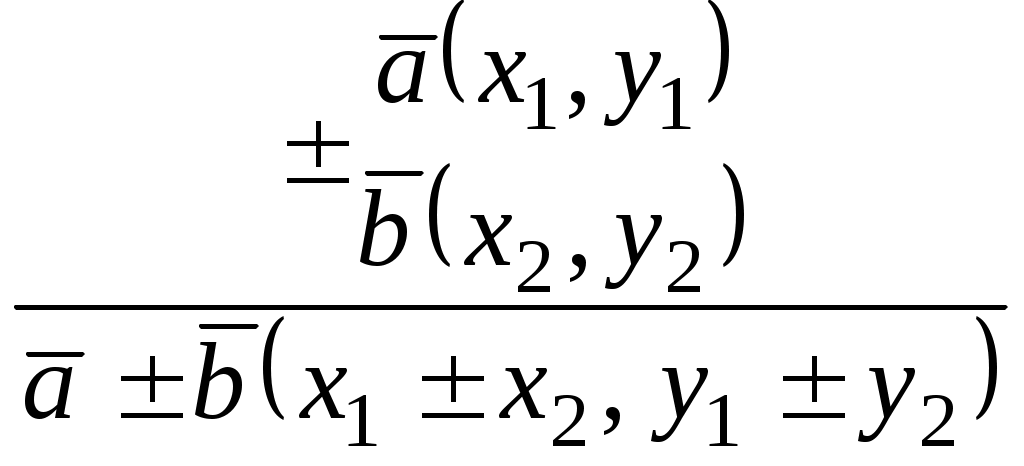Раздел 1. Аналитическая геометрия. Вектор. Тема Вектор. Действия над векторами

• Название: Тема Вектор. Действия над векторами
• Дата: 14.03.2022
• Размер: 0.68 Mb.
• Имя файла: Раздел 1. Аналитическая геометрия. Вектор.doc
• Тип: Документы; #395199

Р А З Д Е Л I
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Тема 1. Вектор. Действия над векторами

заданными длиной и направлениями
Величины, которые полностью определяются своими численными значениями, называются скалярными.

Например: площадь, длина, объем, температура, работа, масса.

Другие величины, например сила, скорость, ускорение определяются не только своими числовыми значениями, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.

Вектор – это направленный отрезок. Вектор обозначается двумя способами.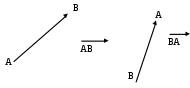




1 ) 2)


Вектор, длина которого равна нулю, называется нулевым вектором и обозначается . Нулевой вектор направления не имеет.
Действия над векторами


I. Сложение векторов
1. Правило треугольника
Возьмем произвольную точку О и построим вектор 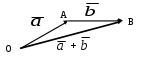. От точки А отложим вектор . Вектор , соединяющий начало первого вектора с концом второго, называется суммой векторов и :







2. Правило параллелограмма
Построим сумму векторов и .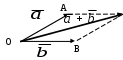

В озьмем произвольную точку О и построим вектора и . Достроим до параллелограмма. Диагональ выходящая из т.О называется суммой векторов.

3. Правило многоугольника
Это правило используется для построения суммы более чем двух векторов. Все вектора откладываются друг за другом.

Построим .

В 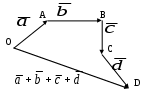озьмем произвольную точку О и построим вектор . От точки А отложим вектор , … , . Вектор , соединяющий начало первого с концом последнего, называется суммой векторов, т.е. .

II. Разность векторов
Построим разность векторов и . Возьмем произвольную точку О и построим вектора и . Вектор , соединяющий конец второго с концом первого вектора .





A

O

В






III. Умножение вектора на число
Умножение вектора на число , есть вектор , длина которого равна , а направление совпадает с направлением , если , и противоположно направлен , если .

Построить .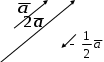






.
Два ненулевых вектора называются коллинеарными, если они лежат на

- ых прямых и их направление либо совпадает, либо противоположно направлены.
IV. Скалярное произведение векторов
Скалярное произведение двух ненулевых векторов и - это число, равное произведению длин этих векторов на косинус угла между ними.




.

.

.

Задача №1
Дано:




..

Построить

.
1 .
2
B
.

Задача №2
Дано:



.

Построить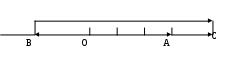








Упражнения
№ 1. Дано:

.

построить




№ 2. Дано:

.

построить





№ 3. Дано:

.

построить




№ 4. Дано:






построить


№5. Дано: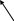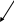





построить




№6. Дано:





построить


№7. Дано:



построить




№8. Дано: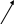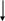





построить







№9. Дано: .

Найти , если угол между векторами и равен:

а) 45⁰; б) 60⁰; в) 120⁰; г) 180⁰.
№10. Дано: .

Найти:

а) ; б) ; в) .
№11. Возьмите два произвольных вектора и , построить

1) ; б) ; 3) ; 4) .
№12.В параллелограмме ABCD:

; . О – точка пересечения диагоналей.

Выразите вектора , , , через и .
№13.Даны векторы , и , причем , , ,

.

Найти:

1) ;

2) .
№14.Вычислите:
1) ;

2) .

Тема 2. Проекция вектора на ось. Координаты вектора.

Действия над векторами с заданными координатами.
П роекцией вектора на ось называется направленный отрезок оси, начало которого есть проекция начала вектора и конец – проекция его конца.
В D

А
C

А₁ В₁ D₁ C₁


Длина этого направленного отрезка берется со знаком «+», если направление отрезка и оси совпадают, и со знаком «–», если их направления противоположны,

т.е.



Проекция вектора на ось 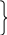равна длине этого вектора умноженной на косинус угла между осью и вектором .

Р
x₂-x₁

y₂-y₁
ассмотрим вектор , где . Спроецируем вектор на ось координат.

У

В

у₂
у₁

А





х₁ х₂ Х




.
Вывод: Координаты вектора это проекции вектора соответствующие

оси координат.

Если начало вектора совпадает с началом координат,

то вектор называется радиус-вектором.
Базис плоскости – это два неколлинеарных вектора этой плоскости, взятые в определенном порядке.

O, ; ; .

Аналогично, базис пространства:

O, ; ; .



– разложение вектора по базису

на плоскости	в пространстве
1) Длина вектора
2) Скалярное произведение векторов
3) Угол между векторами
4) Сумма / разность векторов
5) Умножение вектора на число
,
Условие параллельности векторов
Условие перпендикулярности векторов

Задача
Дано: ;

;

.
Найти: 1) координаты вектора ;

2) длину вектора ;

3) скалярное произведение векторов .
Решение
1)






+



+



_______________________________________________________

.
2) Чтобы найти длину вектора , нужно сначало найти координаты этого вектора:


+



___________________


.
3) Чтобы вычислить скалярное произведение векторов, нужно найти их координаты:



–



__________________


.
Задача №2
Дано: ;

;

;

.

Найти:

1. 
   длину вектора ;
   
2. 
   угол между векторами и .
   

Решение
1) ;

.
2) $

$

; 4

;

;

;

.

Упражнения
№1. Найти угол между векторами и .
№2. Доказать, что с вершинами , и равнобедренный и прямоугольный.
№3. Найти длину вектора , если и .
№4. При каких значениях векторы и коллинеарны ?
№5. Определить при каких значениях вектора и взаимно перпендикулярны?
№6. Даны вершины , и . Определить его внутренние углы.
№7. Дано: ;

;

.

Найти:

1. координаты вектора ;

2. длину вектора ;

3. скалярное произведение векторов 4

4. угол между векторами и .
№8. Дано: ;

;

.

Найти: 1. координаты вектора ;

2. длину вектора ;

3. скалярное произведение векторов и

4. угол между векторами и .
№9. Дано: ;

.

Найти:

1. ;

2. ;

3. ;

4. ;

5. .
№10. Найти скалярное произведение векторов и , и угол между ними:

1) ; 2) ;

2) ; 2) .
№11. При каких значениях вектора и взаимоперпендикулярны?
№12. Найти координаты вектора Б коллинеарного вектора , если :

1) ; ;

2) ; .
№13. Дан треугольник с вершинами , и .

Доказать , что угол тупой.
Зачетная работа

по теме «Вектор. Действия над векторами»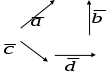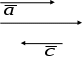

1. 
   Д ано: 2..Дано:
   

Найти: Найти:

; ;

; ;

.
3. Дано: ;

;



Найти:

1. 
   длину вектора ;
   
2. 
   координаты вектора ;
   
3. 
   скалярное произведение векторов .